Lu, C., et al., Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization, in IEEE Conference on Computer Vision and Pattern Recognition. 2016. p. 5249–5257.
本文是这篇 CVPR 会议论文的笔记,主要是对文中的理论方法进行展开详解。本人学术水平有限,文中如有错误之处,敬请指正。
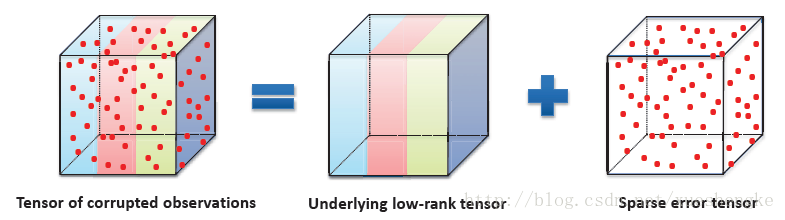
摘要: 此文研究的问题是 Tensor Robust Principal Component Analysis (TRPCA) 问题,其扩展自矩阵的 RPCA 条件。此文的模型基于一个全新的 tensor 奇异值分解(t-SVD),以及其衍生出的 tubal rank 和 tensor 核范数 。考虑已有一个 3 维的 tensor
X∈Rn1×n2×n3
,并满足
X=L0+S0
,其中
L0
是低秩部分而
S0
是稀疏部分。有没有可能同时恢复出两个部分?此文中,作者证明了在特定的合适假设下,可以精确地恢复出低秩和稀疏的部分,通过求解一个凸优化问题,其目标函数为一个核范数和一个
ℓ1
范数的加权和,即
其中 λ=1/max(n1,n2)n3−−−−−−−−−−−√ 。另外,TRPCA 在 n3=1 时就是二维的 RPCA 的简单的优雅的扩展而已。
简介
一个在高维的数据中探索低维结构的问题在图像、文本和视频处理中已经越来越重要,还包括网页搜索,这些数据都是存在于非常高维的数据空间中。经典的 PCA 1 被广泛用于数据分析和维度降低的统计工具中。其计算非常高效,对小的噪声破坏的数据。然而,PCA 最大的问题是对严重的损坏或离异值的观察很脆弱,这些都是真实的数据中随处可见的。虽然很多改进版本的 PCA 被提出了,但是它们均有这很高昂的计算代价。
最近提出的 robust PCA 2 是第一个能实现多项式时间的算法,并有较强的性能保证。假设给定一个数据矩阵
X∈Rn1×n2
,其可以被分解为
X=L0+E0
,其中
L0
是低秩的,
E0
是稀疏的。[2] 表明如果
L0
的奇异向量满足一些非相干性,而
L0
是低秩的并且
E0
是稀疏的,
L0
和
E0
可以很大概率被恢复,通过求解如下的凸问题
其中 ||L||∗ 表示核范数( L 的奇异值之和), ||E||1 表示 ℓ1 范数( E 中所有元素的绝对值之和), λ=1/max(n1,n2)−−−−−−−−−√ 。RPCA 及其扩展已经被成功用于背景建模 [2],视频恢复 3,图像对齐 4 等。
RPCA 的一个主要缺点是其只能处理二维的数据(矩阵)。然而,真实的数据随处可见是高维的,也被记为 tensor 。比如,一幅彩色的图像是一个三维的;一个灰度的视频(两个空间变量,一个时间变量)。为了使用 RPCA,首先要将多维的数据重新转化为矩阵。这样的预处理通常会导致信息损失,造成性能下降。为了改善这样的问题,通常的办法是在高维的数据上进行操作,利用多维结构的优势。
此文中,研究的是 Tensor RPCA,旨在准确地恢复出低秩地 tensor,分离出稀疏地误差,如图所示。
更具体地来说,给定一个 tensor 数据
X
,并知道其可以被分解为
这里 L0 是低秩的, E0 是稀疏的,它们均可以是任意的大小。注意的是这里并不知道 E0 中非零元素的位置,也不知道其数量有多少。考虑的问题是如何高效地分离并恢复出低秩部分和稀疏部分?
期望的是将 low-rank matrix recovery 扩展到 tensor 的情况。然而,这并不容易。主要的问题是如何定义 tensor 的秩,和矩阵的秩不同,它并不能很容易给定。已经有好几种 tensor rank 的定义提出,每种都有缺陷。例如,CP rank 5,定义为秩一 tensor 分解之后的最小值,计算是 NP-hard 。另一个是 Tucker rank [5] 和其凸松弛。对于一个
k
维的 tensor
其中 PΩ(X0) 是一个不全的 tensor,观测到的元素于 Ω 中。[10] 中表明模型 (3) 是次优的:可靠地恢复一个 k 维的长度为
其中 ||E||1 是 E 中所有的元素的绝对值之和。在特定的 tensor 非相干性条件下,首先给出了恢复保证。
最近,12 提出了 tensor tubal rank,基于一个新的 tensor 分解机制 13 14,也被记为 tensor SVD (t-SVD) 。其中定义了一个新的 tensor-tensor 乘积,与矩阵的情况类似。tensor 核范数 15 用于代替 tubal rank 求解 low-rank tensor completion 问题
在此文中,研究的是 TRPCA 问题,其旨在恢复出 L0 和 稀疏部分 E0 从 X=L0+E0∈Rn1×n2×n3 ,通过求解凸优化问题
此文证明只要 L0 的值不太大,并且 E0 是足够稀疏的,该模型 (6) 是可以完美地恢复出低秩部分和稀疏部分。 (6) 中没有需要调节的参数。 λ=1/max(n1,n2)n3−−−−−−−−−−−√ 就能确保恢复准确性。如果 n3=1 ,那么 TRPCA (6) 就简化成了 RPCA (1) 。另一个优势是,其可以被多项式时间算法解决,即交替乘子法 ADMM 16 。
符号与标记
| 符号 | 含义 |
|---|---|
| A | tensor |
| A | 矩阵 |
| a | 向量 |
| a | 标量 |
| 单位矩阵 | |
| R,C | 实数域,复数域 |
| Aijk 或 aijk | 第 i,j,k 个元素 |
| A(i,:,:), A(:,i,:), A(:,:,i) | 第 i 个水平,侧向,正面的切片 |
| 第 i 个正面的切片 | |
| 管道 | |
| ⟨A,B⟩=tr(A∗B) | 矩阵的内积 |
| ⟨A,B⟩=∑n3i=1⟨A(i),B(i)⟩ | tensor 的内积 |
| ||A||1=∑ijk|aijk| | ℓ1 范数 |
| ||A||∞=maxijk|aijk| | 无穷范数 |
| ||A||F=∑ijk|aijk|2−−−−−−−−−√ | Frobenius 范数 |
| ||v||2=∑i|vi|2−−−−−−−√ | ℓ2 范数 |
| ||A||=maxiσi(A) | 谱范数, σi(A) 是矩阵的最大奇异值 |
| ||A||∗=∑iσi(A) | 核范数,奇异值之和 |
| A¯=fft(A,[],3) | 离散傅里叶变换 |
| A=ifft(A¯,[],3) | 离散傅里叶反变换 |
|
A¯=bdiag(A¯)=⎡⎣⎢⎢⎢⎢⎢⎢⎢A¯(1)A¯(2)⋱A¯(n3)⎤⎦⎥⎥⎥⎥⎥⎥⎥
| 块对角矩阵 ,每一个对角块都是一个 A¯ 的正面切片 |
|
bcirc(A)=⎡⎣⎢⎢⎢⎢⎢⎢A(1)A(2)⋮A(n3)A(n3)A(1)⋮A(n3−1)⋯⋯⋱⋯A(2)A(3)⋮A(1)⎤⎦⎥⎥⎥⎥⎥⎥
| 块循环矩阵 bcirc(A)∈Rn1n3×n2n3 |
|
unfold(A)=⎡⎣⎢⎢⎢⎢⎢A(1)A(2)⋮A(n3)⎤⎦⎥⎥⎥⎥⎥, fold(unfold(A))=A
| 展开操作和逆操作 |
t-product
一个维度大小为 n1×n2×n3 的三维 tensor 可以被看作一个 n1×n2 矩阵,其中的每一个元素都是一个沿着第三维的管道。所以,t-product 类似矩阵的乘积,除了循环卷积代替了两个元素的乘积。当 n3=1 时,t-product 简化为矩阵的乘积。所以 RPCA 可以被看作 TRPCA 的一种特殊情况。
共轭转置
A∗∈Rn2×n1×n3
是一个 tensor
A∈Rn1×n2×n3
的共轭转置。其中需要将每一个正面的切片进行共轭转置,并将转置后的切片从第
2
个到 第
单位 tensor
正交 tensor
tensor
Q∈Rn×n×n3
是正交的如果其满足
F-对角 tensor 一个 tensor 的每一个正面的切片都是对角矩阵。
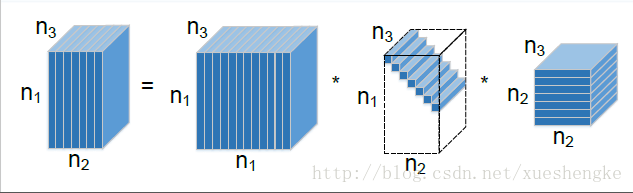
T-SVD
令
A∈Rn1×n2×n3
,其可以被分解为
其中 U∈Rn1×n1×n3 , V∈Rn2×n2×n3 都是正交的, S∈Rn1×n2×n3 是一个 f-对角 tensor 。
注意的是 t-SVD 可以在 傅里叶域内通过矩阵的 SVD 高效地计算得到。根据一个关键的性质:块循环矩阵可以被映射到一个傅里叶域的块对角矩阵,即
其中 Fn3 表示 n3×n3 的离散傅里叶变换矩阵, ⊗ 表示 Kronecker 积。接着,可以对每一个 A¯ 正面的切片进行 SVD 分解操作,即 A¯(i)=U¯(i)S¯(i)V¯(i)∗ ,其中 U¯(i),S¯(i),V¯(i) 分别是 U¯,S¯,V¯ 的正面切片。或者等价的, A¯=U¯S¯V¯∗ 。在对沿着第三维进行傅里叶反变换之后,可以得到 U=ifft(U¯,[],3),S=ifft(S¯,[],3),V=ifft(V¯,[],3) 。
Tensor multi rank 和 tubal rank
A∈Rn1×n2×n3
的 multi rank 定义为一个向量,其第
i
个元素的值是
另外还有一些性质 rankt(A)≤min(n1,n2), rankt(A∗B)≤min(rankt(A),rankt(B)) 。
Tensor 核范数
定义为所有正面切片的矩阵核范数的平均值,
||A||∗:=1n3∑n3i=1||A¯(i)||∗
。这里有一个因子
1/n3
,此文提出的模型与之前的研究不同。该 tensor 核范数定义在傅里叶变换域,那么其非常接近原来的块循环矩阵的核范数,如下
(12) 给出了一个直接的关系式,计算 tensor 核范数,块循环矩阵非常的重要。
Tensor 谱范数 谱范数定义为 ||A||:=||A¯|| ,矩阵的最大奇异值。
Tensor 标准基 列基,记为 e˚i 是一个 n×1×n3 的 tensor,其中第 (i,1,1) 个元素值为 1,其他都为零。那么其转置 e˚∗ 是行基。tube 基,记为 e˙k 是一个 1×1×n3 的 tensor,其第 (1,1,k) 个元素等于1,而其他都为零。为了方便,记 eijk=e˚i∗e˙j∗e˚∗k ,并且有 A=∑ijk⟨eijk,A⟩eijk=∑ijkaijkeijk 。
Tensor 非相干条件
对于
L0∈Rn1×n2×n3
,假设
rankt(L0)=r
,并其 skinny t-SVD
L0=U∗S∗V∗
,其中
U∈Rn1×r×n3
,
V∈Rn2×r×n3
满足
U∗∗U=I, V∗∗V=I
,并且
S∈Rr×r×n3
是一个 f-对角 tensor 。
L0
会满足 tensor 非相干条件,如果
算法 1 求解
(6)
通过 ADMM
输入: tensor 数据
X
,参数
λ
。
初始化:
L0=S0=Y0=0, ρ=1.1, μ0=1e−3, μmax=1e10, ϵ=1e−8
。
while not converged do
1. 更新
Lk+1
:
2. 更新 Ek+1 :
3. Yk+1=Yk+μk(Lk+1+Ek+1−X) ;
4. 更新 μk+1=min(ρμk,μmax) ;
5. 检查收敛条件:
end while
实验
详见原文
- I. Jolliffe. Principal component analysis. Wiley Online Library, 2002. ↩
- E. J. Cand`es, X. D. Li, Y. Ma, and J. Wright. Robust principal component analysis? Journal of the ACM, 58(3), 2011. ↩
- H. Ji, S. Huang, Z. Shen, and Y. Xu. Robust video restoration by joint sparse and low rank matrix approximation. SIAM Journal on Imaging Sciences, 4(4):1122–1142, 2011. ↩
- Y. Peng, A. Ganesh, J. Wright, W. Xu, and Y. Ma. RASL: Robust alignment by sparse and low-rank decomposition for linearly correlated images. TPAMI, 34(11):2233–2246, 2012. ↩
- T. G. Kolda and B. W. Bader. Tensor decompositions and applications. SIAM Review, 51(3):455–500, 2009. ↩
- J. Liu, P. Musialski, P. Wonka, and J. Ye. Tensor completion for estimating missing values in visual data. TPAMI, 35(1):208–220, 2013. ↩
- S. Gandy, B. Recht, and I. Yamada. Tensor completion and low-n-rank tensor recovery via convex optimization. Inverse Problems, 27(2):025010, 2011. ↩
- M. Signoretto, Q. T. Dinh, L. De Lathauwer, and J. A. Suykens. Learning with tensors: a framework based on convex optimization and spectral regularization. Machine Learning, 94(3):303–351, 2014. ↩
- R. Tomioka, K. Hayashi, and H. Kashima. Estimation of low-rank tensors via convex optimization. arXiv preprint arXiv:1010.0789, 2010. ↩
- C. Mu, B. Huang, J. Wright, and D. Goldfarb. Square deal: Lower bounds and improved relaxations for tensor recovery. arXiv preprint arXiv:1307.5870, 2013. ↩
- B. Huang, C. Mu, D. Goldfarb, and J. Wright. Provable low-rank tensor recovery. Optimization-Online, 4252, 2014. ↩
- Z. Zhang, G. Ely, S. Aeron, N. Hao, and M. Kilmer. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In CVPR, pages 3842–3849. IEEE, 2014. ↩
- K. Braman. Third-order tensors as linear operators on a space of matrices. Linear Algebra and its Applications, 433(7):1241–1253, 2010. ↩
- M. E. Kilmer and C. D. Martin. Factorization strategies for third-order tensors. Linear Algebra and its Applications, 435(3):641–658, 2011. ↩
- O. Semerci, N. Hao, M. E. Kilmer, and E. L. Miller. Tensorbased formulation and nuclear norm regularization for multienergy computed tomography. TIP, 23(4):1678–1693, 2014. ↩
- S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends ® in Machine Learning, 3(1):1–122, 2011. ↩