leetcode98. 验证二叉搜索树

题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

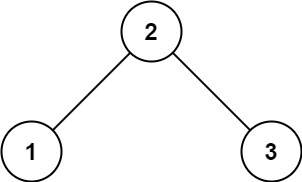
输入：root = [2,1,3]
输出：true

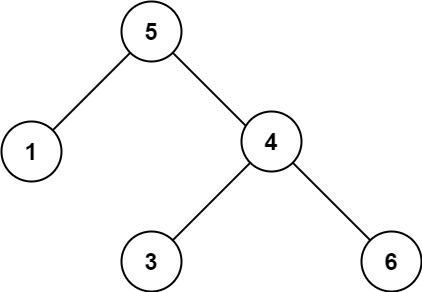
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

思路和代码：

首先这题的解决办法可以分为两种，递归和迭代。

怎么判断一棵树是不是二叉搜索树？二叉搜索树的中序遍历是有序的。所以中序遍历，依次处理节点发现其严格递增，则必然是二叉搜索树。

一.递归

1.递归序

简单回顾一下二叉树的前中后序遍历的递归实现。

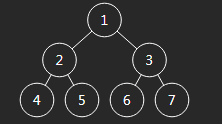
对于这样的一棵二叉树，它的递归序是什么？

def f(root):
    # 空节点就返回
    if not root:
        return root
    # 1.以上两行代码是第一次来到自己
    # 左边递归遍历
    f(root.left)
    # 2.第二次来到自己 左树遍历完了之后得回到自己 然后才能调用下一句
    # 右边递归遍历
    f(root.right)
    # 3.第三次来到自己 右树遍历完了之后第三次回到自己 只有回到自己才知道下行没语句了 自己才能返回
   

以上面的二叉树为例，先得到1,2,4,发现4的左边点为空，则第二次回到4,4的右节点为空，第三次回到4，此时序列是1,2,4,4,4。

2的左子树遍历完了之后又回到2，遍历2的右节点5, 5的做节点为空，第二次到5, 5的右节点为空，第三次到5…以此类推，得到最终的递归序是——

1,2,4,4,4,2,5,5,5,2,1,3,6,6,6,3,7,7,7,3,1。

对于每一个节点都会有三次遍历。

2.二叉树的前中后序递归实现

而前（先）序遍历是第一次遍历到该节点的时候处理节点（打印或者加到结果集中）；中序是第二次遍历到该节点的时候处理节点；后续是第三次遍历到该节点的时候处理节点。

递归实现前序遍历（leetcode144）：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        def preOrder(root):
            if not root:
                return []
            res.append(root.val)
            preOrder(root.left)
            preOrder(root.right)
        res = []
        preOrder(root)
        return res

递归实现中序遍历的代码（leetcode94）：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        def inOrder(root):
            if not root:
                return res
            inOrder(root.left)
            res.append(root.val)
            inOrder(root.right)
        res = []
        inOrder(root)
        return res

递归实现后序遍历（leetcode145）：

class Solution