https://blog.csdn.net/akadiao/article/details/79551180
https://blog.csdn.net/wgj99991111/article/details/84708255
在训练神经网络时,当需要查看一个张量在训练过程中值的分布情况时,可通过tf.summary.histogram()将其分布情况以直方图的形式在TensorBoard直方图仪表板上显示.
tf.summary.histogram
tf.summary.histogram():
输出一个直方图的Summary protocol buffer .
参数
name:生成的节点名称.作为TensorBoard中的一个系列名称.
values:一个实数张量.用于构建直方图的值.
collections:图形集合键的可选列表.添加新的summary操作到这些集合中.默认为GraphKeys.SUMMARIES.
family: summary标签名称的前缀,用于在Tensorboard上显示的标签名称.(可选项)
tf.summary.histogram()将输入的一个任意大小和形状的张量压缩成一个由宽度和数量组成的直方图数据结构.假设输入 [0.5, 1.1, 1.3, 2.2, 2.9, 2.99],则可以创建三个bin,分别包含0-1之间/1-2之间/2-3之间的所有元素,即三个bin中的元素分别为[0.5]/[1.1,1.3]/[2.2,2.9,2.99].
这样,通过可视化张量在不同时间点的直方图来显示某些分布随时间变化的情况.
示例
以下为tensorflow文档中提供的示例.在该例子中每次创建一个均值变化的正态分布(采样1000次),标准差为1,均值随循环次数的增加而增加.在直方图中可以看到每步均值的变化.
#!/usr/bin/python
# coding:utf-8
# TensorBoard直方图仪表板
import tensorflow as tf
k = tf.placeholder(tf.float32)
# 创建一个均值变化的正态分布(由0到5左右)
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# 将该分布记录到直方图汇总中
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
summaries = tf.summary.merge_all()
# 设置一个循环并将摘要写入磁盘
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)
通过在终端输入:
tensorboard --logdir=/tmp/histogram_example
可以在TensorBoard中查看结果.
直方图模式
其中,直方图模式有两种:OVERLAY和OFFSET.
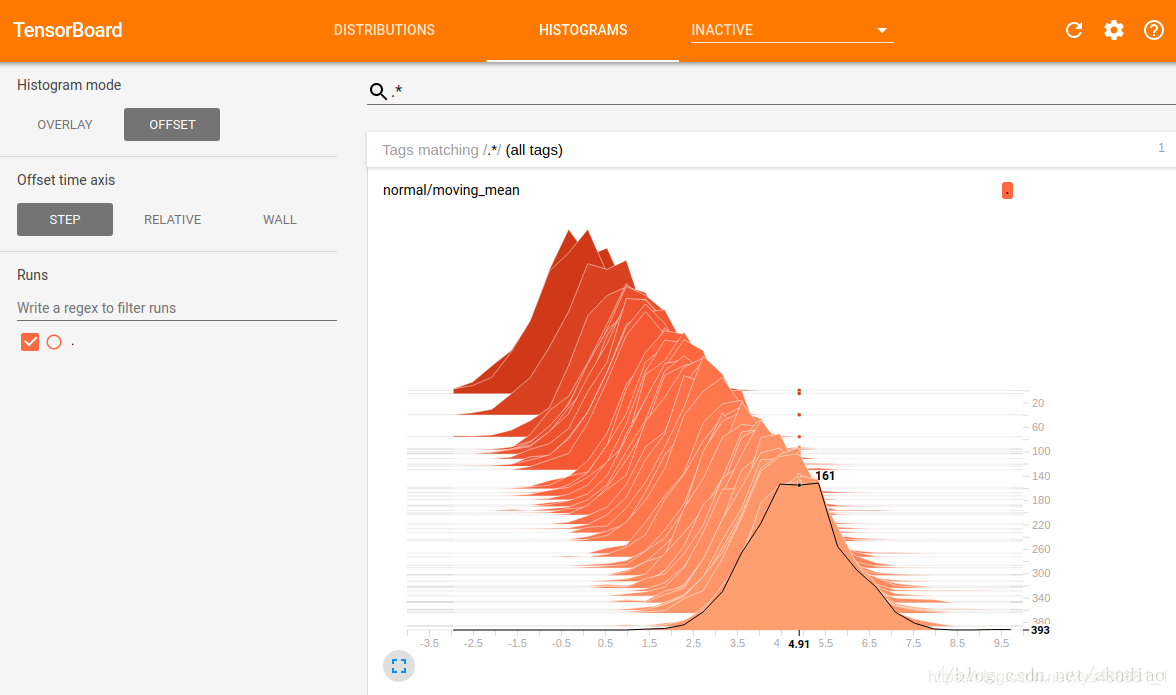
OFFSET模式:
其中,横轴表示值,纵轴表示数量,每个切片显示一个直方图,切片按步骤(步数或时间)排列;旧的切片较暗,新的切片颜色较浅.如图,可以看到在第393步时,以4.91为中心的bin中有161个元素.
另外,直方图切片并不总是按步数或时间均匀分布,而是通过水塘抽样/reservoir sampling来抽取所有直方图的一个子集,以节省内存.
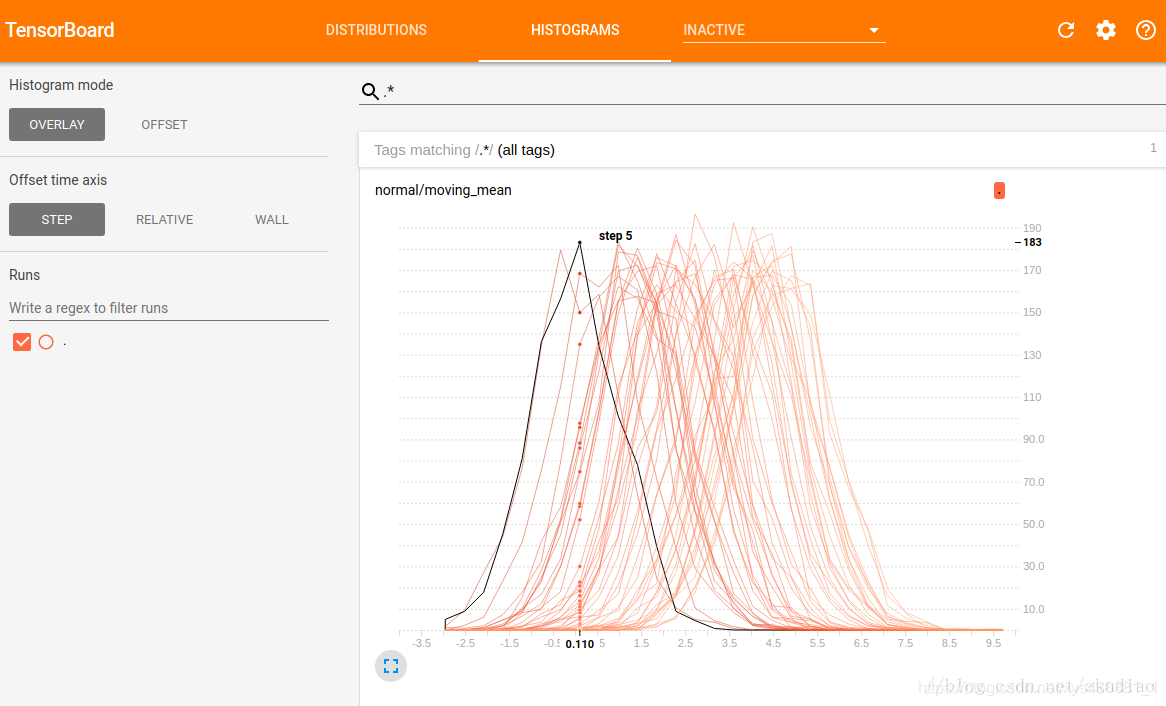
OVERLAY模式:
其中,横轴表示值,纵轴表示数量.各个直方图切片不再展开,而是全部绘制在相同的y轴上.这样不同的线表示不同的步骤(步数或时间).如图,可以看到在第5步时,以0.11为中心的bin中有183个元素.
OVERLAY模式用于直接比较不同直方图的计数.
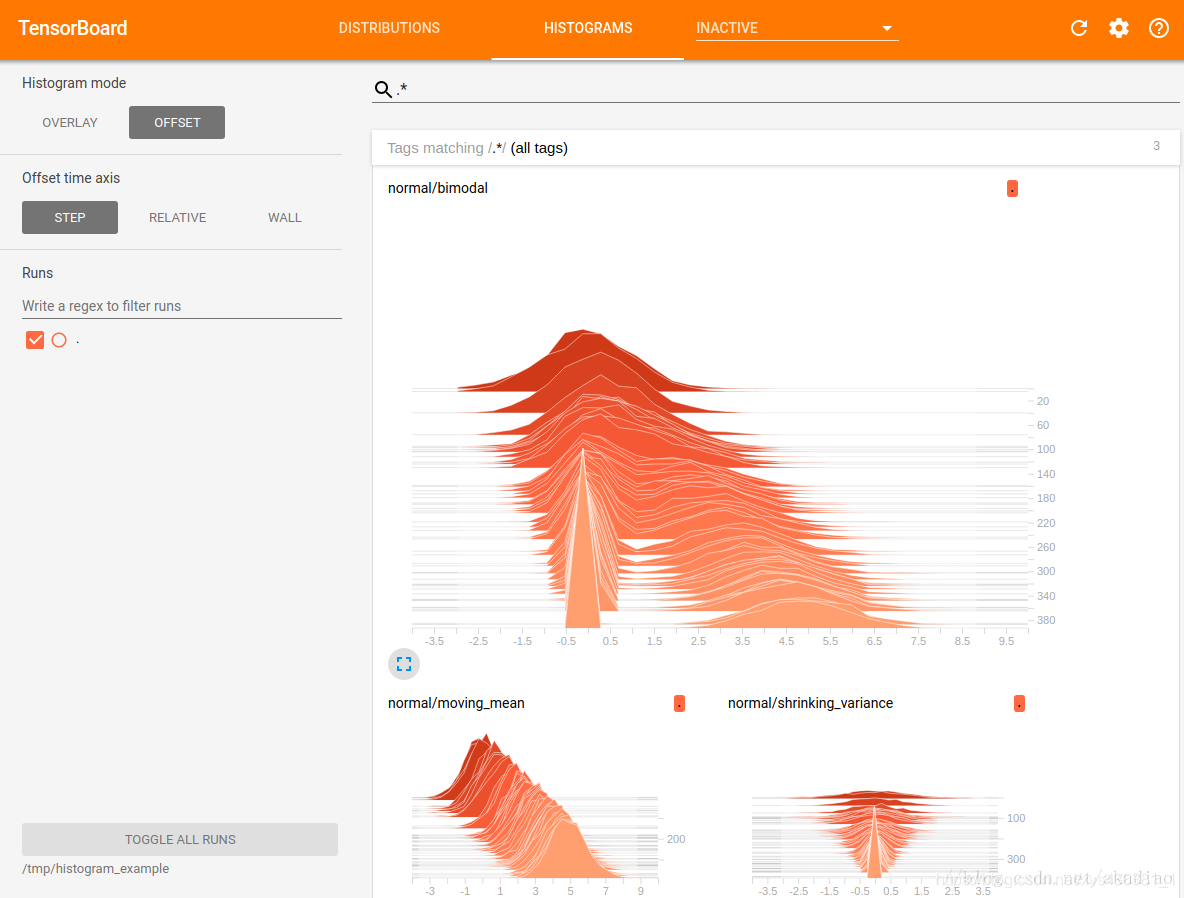
多模式分布
直方图仪表板非常适合可视化多模式分布,通过连接两个不同正态分布(一个移动均值的正态分布和一个缩小方差的正态分布)的输出来构造一个简单的双峰分布.如下所示:
#!/usr/bin/python
# coding:utf-8
import tensorflow as tf
k = tf.placeholder(tf.float32)
# 创建一个均值变化的正态分布
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# 将该分布记录到直方图summary中
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# 创建一个方差递减的正态分布
variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k))
# 记录分配
tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal)
# 将两种分布组合成一个数据集
normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0)
# 添加另一个直方图summary来记录组合分布
tf.summary.histogram("normal/bimodal", normal_combined)
summaries = tf.summary.merge_all()
# 设置会话和摘要作者
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
# 设置一个循环并将摘要写入磁盘
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)
可以得到两组单独的正太分布和连接起来后形成的一组双峰结构分布的图表.
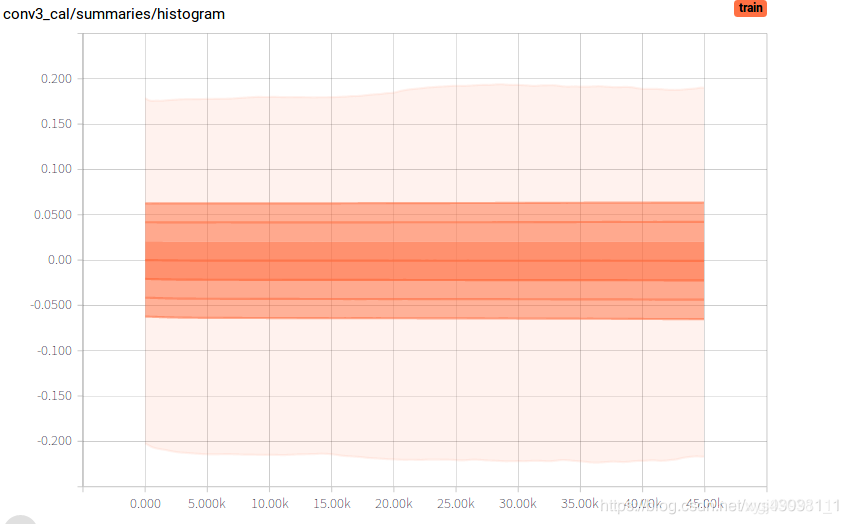
distributions显示内容解析
distributions图和histogram图显示的数据源是相同的,只是用不同的方式对相同的内容进行展示。在网上找了很久也没要找到关于distributions图的详解,下面写写自己对该图的理解:
该图的横坐标为训练的次数,纵坐标为权重值的取值范围,图中首先从整体上显示了在训练过程中权重值的取值范围,然后用不同的颜色表示取某个区域值的频次,颜色越深表示出现的频次越多。从上图可以看出,该权重值在0附近颜色最深,也就是说在0附近这个区域权重值的取值频次最高。