目录
一、LeetCode 977.有序数组的平方
题目链接:977.有序数组的平方
文章讲解:代码随想录
视频讲解: https://www.bilibili.com/video/BV1QB4y1D7ep
思路
题目要求将数组平方并排序,可简单地使用内置函数nums.sort()实现如下程序
#Python
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
for i in range(len(nums)):
nums[i] = nums[i]**2
nums.sort()
return nums
该算法时间复杂度为O(n+nlogn)
然而本章内容着重于数组与双指针的使用,因此对于排序部分进一步编写算法。
注意到题目中给出的原数组已经为升序,那么平方后最大数必定在nums[0]^2与 nums[n-1]^2之间,并且从两端向中间,平方后的数字一次变小,以此为依据设计双指针算法:
设置指针l, r分别指向原数组两端,判断nums[0]^2与 nums[n-1]^2大小,将较大的一个置于新数组尾部(升序排列),然后调整l或r继续循环比较,直到平方并排序后的数组sortedList生成完毕
C++代码
//双指针
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int n = nums.size();
vector<int> ans(n);
int i = 0, j = n - 1;
for (int p = n - 1; p >= 0; p--) {
int x = nums[i] * nums[i];
int y = nums[j] * nums[j];
if (x > y) {
ans[p] = x;
i++;
} else {
ans[p] = y;
j--;
}
}
return ans;
}
};
Python代码
#双指针
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
l, r, k = 0, len(nums)-1, len(nums)-1
sortedList = [0]*(r+1)
while(k >= 0):
if(nums[l]**2 > nums[r]**2):
sortedList[k] = nums[l]**2
l += 1
k -= 1
else:
sortedList[k] = nums[r]**2
r -= 1
k -= 1
return sortedList
小结
上述使用双指针的算法时间复杂度为O(n),总体上是优于直接使用内置排序函数O(n + nlogn)的
二、LeetCode 209.最小长度的子数组
题目链接:209.最小长度的子数组
思路
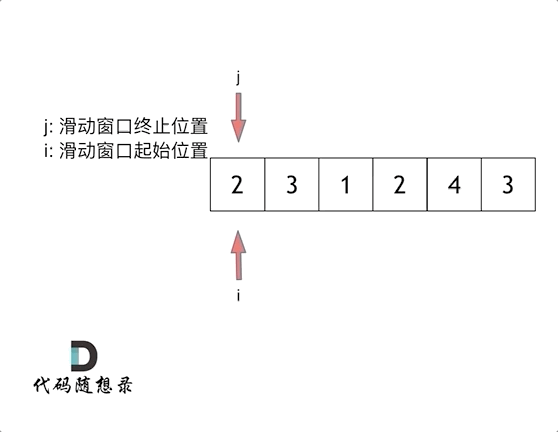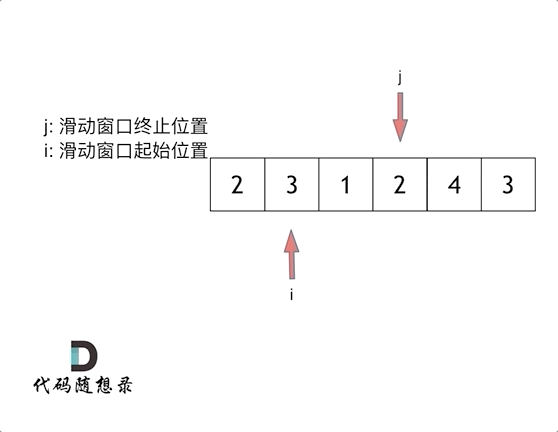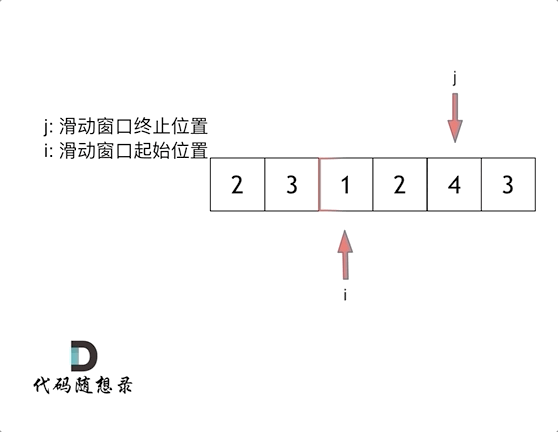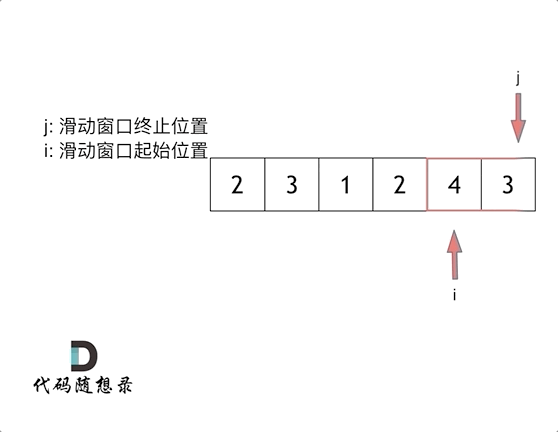
滑动窗口: 使用一前一后双指针
f, r确定一个具体的限定区间,并通过不断调整前后指针的值实现区间的移动。双指针限定的移动区间形似一个窗口形式
滑动窗口的特性很适合求解子数组或获取连续平滑数据的问题,因此很适合本题的情形。
首先需要注意审题,要求找出该数组中满足其 总和大于等于 target 的长度最小的子数组,并非等于,因此设计程序时需要注意判断条件;
其次,本题求解的主体为连续的一段子数组,我们引入滑动窗口进行求解。设立双指针f, r限定窗口范围;sum_win用于存放当前窗口内数字总和;short存放当前满足条件的最短子数组长度。
通过判断sum_win与target的大小关系,移动窗口左右指针,并实时更新sum_win与short的值:
当sun_win >= target时,满足条件,若当前数组长度更短,则更新short值,并尝试后移f,寻找更短数组长度;
当sum_win < target时,不满足条件,后移r,直到满足条件或超出数组范围停止。
C++代码
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int r = 0, l = 0, shlen = nums.size()+1;
int sum = nums[0];
while(r < nums.size() && l < nums.size()){
if(sum >= target){
shlen = min(r-l+1, shlen);
sum -= nums[l];
l++;
}
else if(sum < target){
r++;
if(r < nums.size())sum += nums[r];
}
}
return shlen%(nums.size()+1);
}
};
Python代码
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
f = r = 0
sum_win, short = nums[0], len(nums)+1
while(r < len(nums)):
if(sum_win < target):
r += 1
if(r != len(nums)):
sum_win += nums[r]
else:
short = min(short, r-f+1)
sum_win -= nums[f]
f += 1
return short%(len(nums)+1)
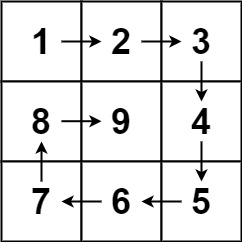
三、LeetCode 59.螺旋矩阵II
题目链接: 59.螺旋矩阵II
文章讲解:代码随想录
视频讲解:https://www.bilibili.com/video/BV1SL4y1N7mV/
题目要求对正整数 n ,生成一个包含 1 到
n
2
n^2
n2 所有元素,且元素按顺时针顺序螺旋排列的
n
×
n
n × n
n×n 正方形矩阵 matrix
思路一
可以将矩阵生成当做一个动态的坐标移动过程,当碰到边界或前方坐标点已经填入过数字时改变方向向量;
由于每次坐标移动只涉及一个方向,因此设立bool格式的row变量来控制
x
x
x 增量或
y
y
y 增量,row = ture时
x
x
x 变化,反之则
y
y
y 变化;使用d作为每次的增量,初始值为
1
1
1;
观察上图螺旋矩阵生成过程可以发现规律:增量大小d仅在每次row = false → true时变为 -d , 即每次
y
y
y 变化结束后变为原增长量的负值。因此在每次 纵向变化(
y
y
y 变化)结束后增加一条指令d = -d使得增量变负即可。
C++代码
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> matrix(n, vector<int>(n));
int x = 0, y = 0, d = 1;
bool row = true;
for(int i = 1; i <= pow(n, 2); i++){
matrix[y][x] = i;
if(row){
if(x+d == n|| x+d == -1 || (x+d != n && x+d != -1 && matrix[y][x+d] != 0)){
row = false;
y += d;
}
else{
x += d;
}
}
else{
if(y+d == n || (y+d != n && matrix[y+d][x] != 0)){
row = true;
d = -d;
x += d;
}
else{
y += d;
}
}
}
return matrix;
}
};
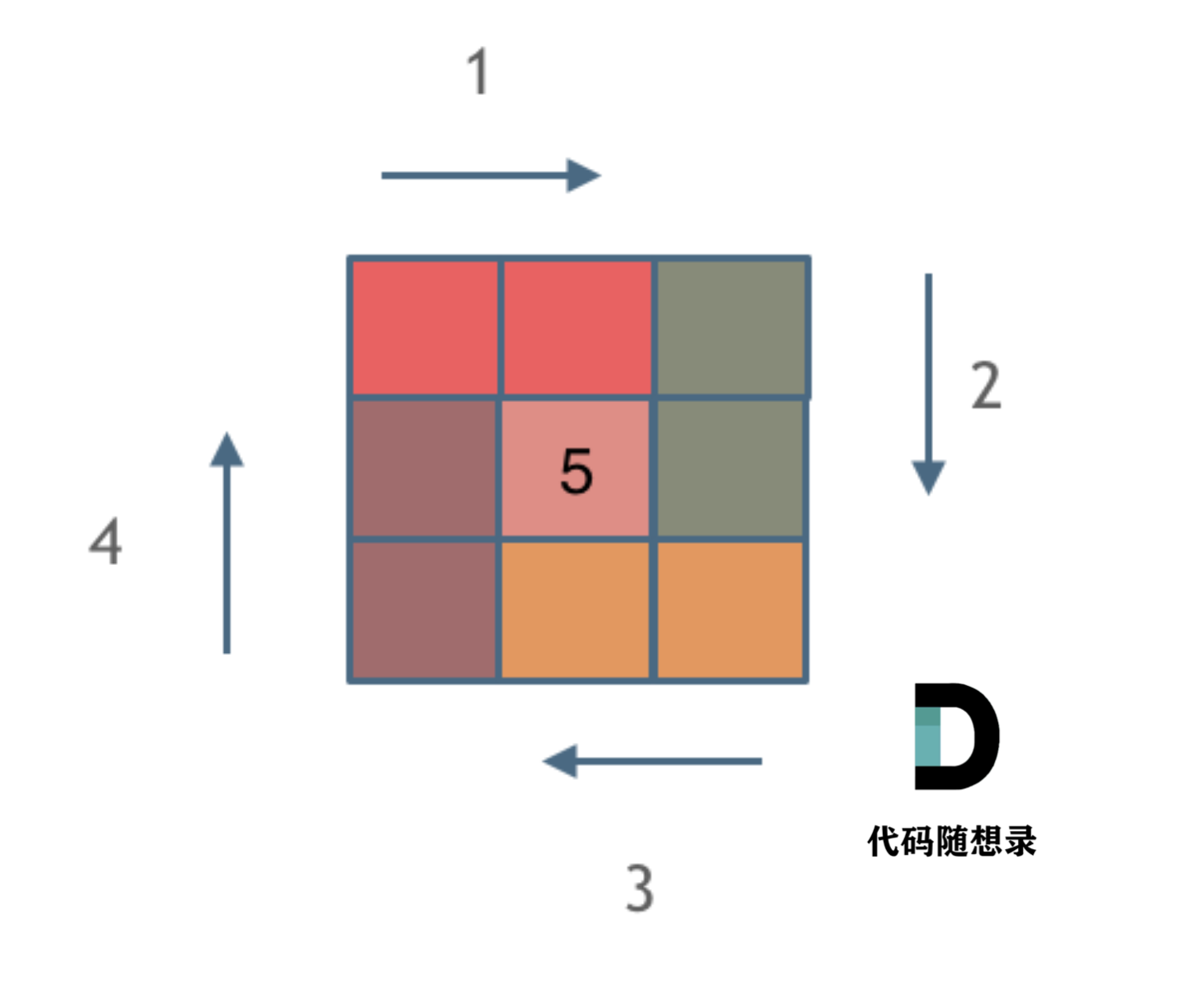
思路二
将螺旋矩阵的生成看做每一圈正方形外围的填充,每一圈在填充时分为上、右、下、左四个部分;每一圈填充时,设立好四个方向的边界,不断循环迭代即可;在数字等于
n
2
n^2
n2 时停止迭代。
Python代码
class Solution(object):
def generateMatrix(self, n):
if n <= 0:
return []
# 初始化 n x n 矩阵
matrix = [[0]*n for _ in range(n)]
# 初始化边界和起始值
top, bottom, left, right = 0, n-1, 0, n-1
num = 1
while top <= bottom and left <= right:
# 从左到右填充上边界
for i in range(left, right + 1):
matrix[top][i] = num
num += 1
top += 1
# 从上到下填充右边界
for i in range(top, bottom + 1):
matrix[i][right] = num
num += 1
right -= 1
# 从右到左填充下边界
for i in range(right, left - 1, -1):
matrix[bottom][i] = num
num += 1
bottom -= 1
# 从下到上填充左边界
for i in range(bottom, top - 1, -1):
matrix[i][left] = num
num += 1
left += 1
return matrix
四、数组章节总结
数组:数组是存放在连续内存空间上的相同类型数据的集合,最基础的数据结构
注意要点
- 数组下标都是从0开始的
- 数组内存空间的地址是连续的
- 数组的元素是不能删的,只能覆盖(固定的一段内存空间)
数组问题经典方法
二分法
基本思想:设置左右两个端值指针,确定中间位置middle,通过使用middle对两个端值指针进行更新,达到缩小区间的目的
暴力解法时间复杂度:O(n)
二分法时间复杂度:O(logn)
二分法是算法面试中的常考题,建议通过这道题目,锻炼自己手撕二分的能力。
双指针法
双指针法(快慢指针法):通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
暴力解法时间复杂度:O(n^2)
双指针时间复杂度:O(n)
在本章题目中有如下要点:
- 数组在内存中是连续的地址空间,不能释放单一元素,如果要释放,就是全释放(程序运行结束,回收内存栈空间)。
- C++中vector和array的区别一定要弄清楚,vector的底层实现是array,封装后使用更友好。
双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法。
滑动窗口
介绍见本文 二、LeetCode 209.最小长度的子数组:滑动窗口
暴力解法时间复杂度:O(n^2)
滑动窗口时间复杂度:O(n)
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。