ANLNet
Introduction
《ANLNet:Asymmetric Non-local Neural Networks for Semantic Segmentation》发表于ICCV 2019,是基于Non-Local的思路往轻量化方向做改进。**Non-Local模块是一种效果显著的技术,但同时也受限于过大计算量而难以很好地嵌入网络中应用。为了解决以上问题,ANLNet基于Non-Local结构并融入了金字塔采样模块,在不牺牲性能的情况下极大减少计算量和内存负担,得到APNB模块,在充分考虑了长距离依赖的前提下,对APNB做修改,融入了不同层次的特征,得到AFNB,从而在保持性能的同时极大地减少计算量。
code:https://github.com/MendelXu/ANN.git.
- 结合SPP和Non-Local,前者从不同大小区域内提取出关键点,后者对这些关键点建模长距离依赖;
- Non-Local 需要计算每一个像素点,可以看作是点对点建模;ANL-Net只计算通过SPP提取出的关键点,可以看作是点对区域建模;
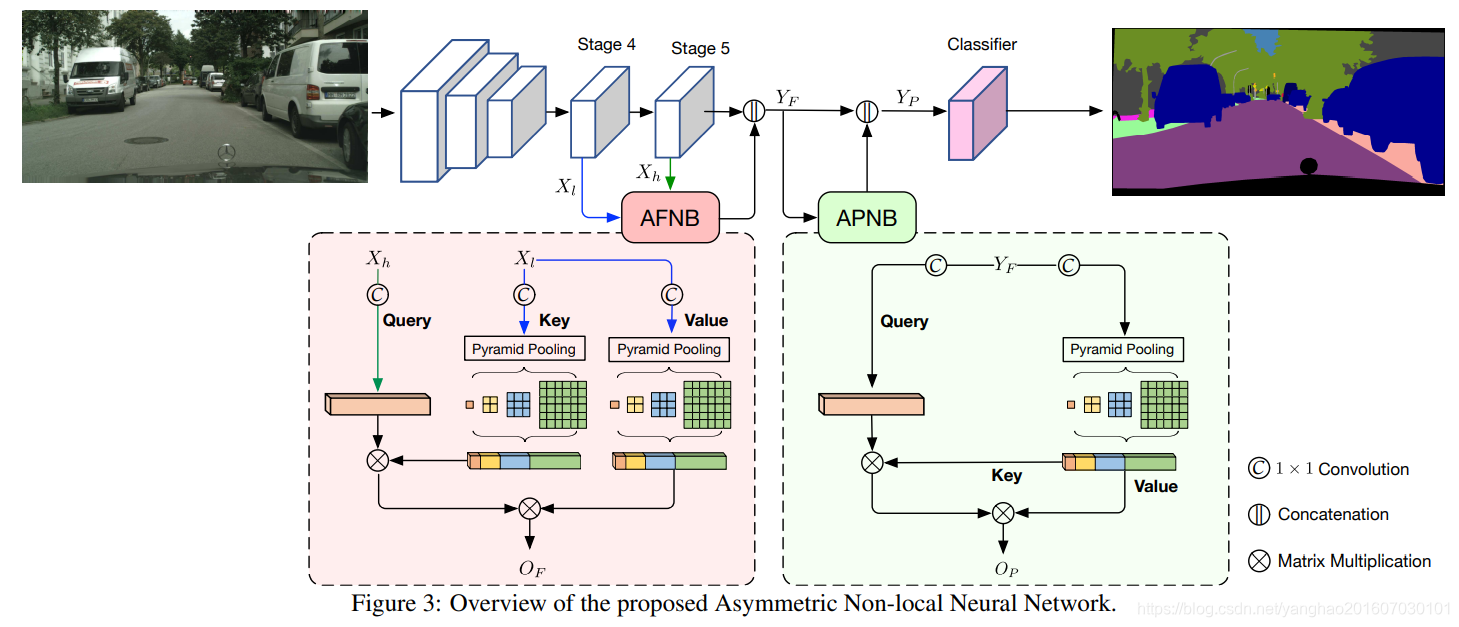
- AFNB包含两个输入,一个高级特征图,一个低级特征图,分别对应图中的Stage5和Stage4。其中高级特征图作为Query,低级特征图作为Key和Value;
- APNB的建模方式与AFNB类似。
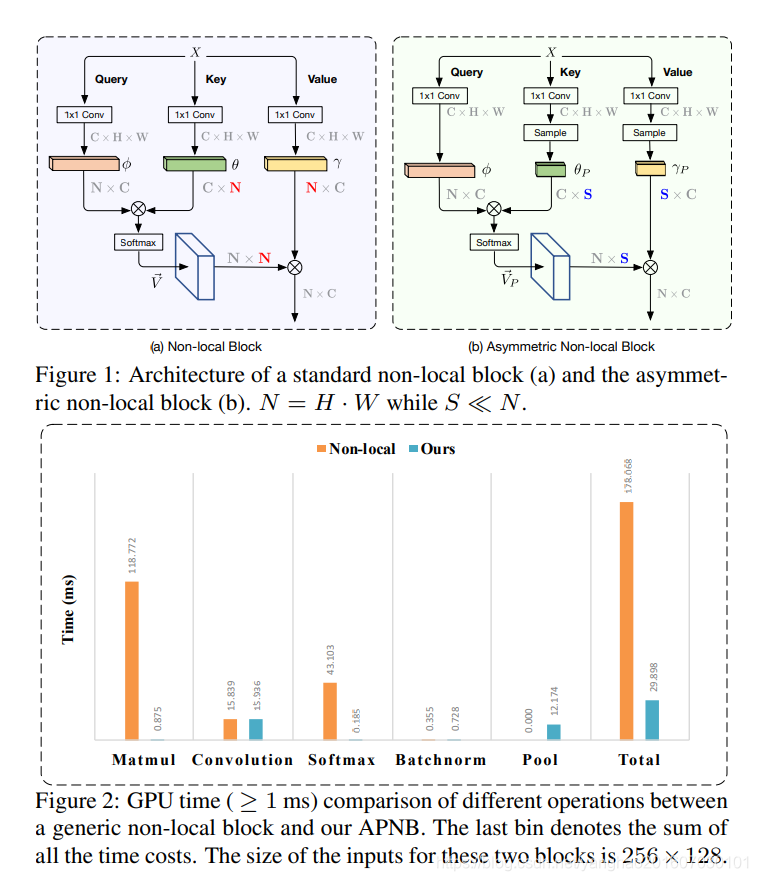
Non-local 的不足:一个不同的non-local块如上图a所示。该块首先要计算所有位置之间的相似性,这需要通过矩阵相乘运算得到,给定一个尺寸为C×H×W的输入特征图,其计算复杂度为 O ( C H 2 W 2 ) O(CH^2W^2) O(CH2W2)。之后它还需要gather所有位置对它们的影响,这一步的计算复杂度也是 O ( C H 2 W 2 ) O(CH^2W^2) O(CH2W2)。显然,这种方式的很不高效,高昂的计算代价使得它很难在实际中使用。于是及需要一个不牺牲其性能,同时更加高效的work。
作者观察到只要key分支和value分支的输出有相同的尺寸,non-local block最终的输出尺寸就不会变化。所以如果key分支和value分支值取少量的表示性点,即将图1 a中比较大的N值变成b中的一个小很多的S,这样就可能实现不牺牲性能的情况下极大地减小复杂度,。这一思想就是该work中的核心创新思想。
具体到如何选择更少的表示性点,这里将spatial pyramid pooling嵌入到non-local blocks中来实现(APNB)。APNB和 标准non-local block的cost比较见图2。
此外,作者在APNB的基础上融合了不同stages的特征,得到AFNB,旨在计算low-level和high-level 特征图之间每个像素的关系,从而生成了一个带有long range interactions的融合特征。
一些work表明,充分利用 long range dependencies能够提高性能,但是由于增加一个卷积层感受野也不足以覆盖相关区域,而且加深网络深度或选择一个更大的kernel来增加感受野的方式会带来很大的计算代价,很不高效,所以只是依赖卷积来捕获long range dependencies是受限的
Asymmetric Non-local Neural Network
论文中受限回顾了non-local的详细设计细节,然后介绍Asymmetric Pyramid Non-local Block,Asymmetric Fusion Non-local Block。
Revisiting Non-local Block
如图1所示,假设输入特征 X ∈ R C × H × W X \in R^{C×H×W} X∈RC×H×W,然后使用3个1×1卷积 W ϕ ( X ) , W Θ , W γ W_\phi(X),W_\Theta,W_\gamma Wϕ(X),WΘ,Wγ来将X变成不同的embeddings :
ϕ = W ϕ ( X ) , θ = W θ ( X ) , γ = W γ ( X ) , 这 里 ϕ , θ , γ ∈ R C ^ × H × W 。 \phi = W_\phi(X),\theta= W_\theta(X),\gamma=W_\gamma(X),这里\phi,\theta,\gamma \in R^{\hat{C}×H×W}。 ϕ=Wϕ(X),θ=Wθ(X),γ=Wγ(X),这里ϕ,θ,γ∈RC^×H×W。
C ^ \hat{C} C^是生成的新embeddings的通道数量(一般比C小,这里降维了),接下来,三个embeddings被flatten到 C ^ × N , N = H ⋅ W \hat{C}×N,N=H·W C^×N,N=H⋅W。然后通过矩阵相乘 V = ϕ T × θ V=\phi^T × \theta V=ϕT×θ得到一个相似性矩阵 V ∈ R N × N V\in R^{N×N} V∈RN×N.
之后,还会再V上做一个正则化操作得到一个统一的相似性矩阵, V → \mathop{V}\limits ^{\rightarrow} V→这里正则化函数选择的是softmax,等价于self-attention机制,再许多任务中都适用。
对于γ中的每个位置,attention层的输出是: O = V → × γ T O = \mathop{V}\limits ^{\rightarrow}×\gamma^T O=V→×γT 。这的 O ∈ R N × γ T O \in R^{N×\gamma^T} O∈RN×γT。最后的输出为:
Y = W o ( O T ) + X o r Y = c a t ( W 0 ( O T ) , X ) . Y=W_o(O^T)+X or Y =cat(W_0(O^T),X). Y=Wo(OT)+XorY=cat(W0(OT),X).
W o W_o Wo由一个1×1卷积实现,作为一个权重参数来调整 non-local 操作相对于原始输入X的重要性,更重要的是讲通道从 C ^ \hat{C} C^恢复到原始输入X的通道数C。
Asymmetric Pyramid Non-local Block
前面提到了,为了减少Non-local的计算复杂度和内存消耗,将key分支和value分支值取少量的表示性点,即由原来的N到S。这里具体的数据流公式表示如下面:
将N变成S后:
Solution。所以,关键就变成了如何选取S个点。这里是在θ和γ之后分别增加采样模块 P θ P_\theta Pθ来采样几个稀疏的anchor点,表示为 θ P ∈ R c ^ × S , γ P ∈ R c ^ × S \theta_P \in R^{\hat{c}×S},\gamma_P \in R^{\hat{c}×S} θP∈Rc^×S,γP∈Rc^×S。这里的S就是要采样的点数。数学表示如下:
θ P = P θ ( θ ) , γ P = P γ ( γ ) . \theta_P=P_\theta(\theta),\gamma_P=P_\gamma(\gamma). θP=Pθ(θ),γP=Pγ(γ).
ϕ 和 a n c h o r 点 θ p \phi 和anchor点\theta_p ϕ和anchor点θp之间的相似性矩阵 V P V_P VP的可以由下计算:
V P = ϕ T × θ p V_P=\phi^T × \theta_p VP=ϕT×θp
这里计算得到的相似性矩阵 V P V_P VP是一个非对称矩阵,size为N×S。随后的步骤和标准的Non-local一样,对 V P V_P VP做正则化,然后和 γ P T \gamma _P^T γPT相乘得到最终的attention输出 O = V P → × γ P T O = \mathop{V_P}\limits ^{\rightarrow}×\gamma_P^T O=VP→×γPT。最后最终的输出为
Y P = c a t ( W 0 ( O P T ) , X ) . Y_P=cat(W_0(O_P^T),X). YP=cat(W0(OPT),X).
这样相比原来 O ( C ^ N 2 ) 的 复 杂 度 , 现 在 复 杂 度 为 O ( C ^ N S ) , 计 算 复 杂 度 为 原 来 的 S N O(\hat{C}N^2)的复杂度,现在复杂度为O(\hat{C}NS), 计算复杂度为原来的\frac{S}{N} O(C^N2)的复杂度,现在复杂度为O(C^NS),计算复杂度为原来的NS,理想情况下S要足够小才能极大的减小计算复杂度,但是通道的减少可能会找出性能的下降,所以这里利用SPP空间金字塔池化来选点,这样即能够减少点, 也能够利用SPP的全局表示能力保证性能不下降,而且SPP是parameter-free且高效的。
于是得到了图3中的设计:
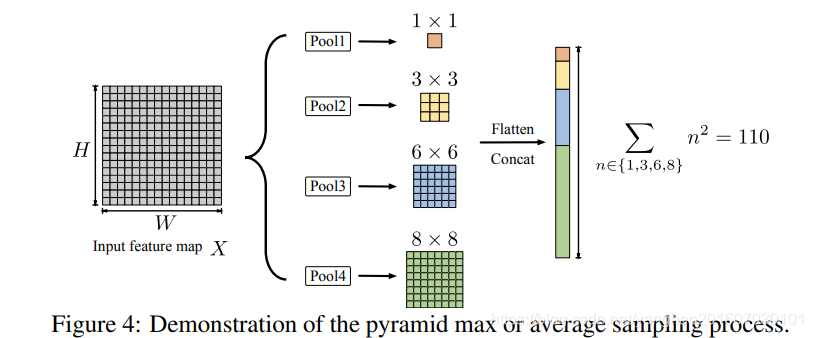
其中关键的改变就是θ和γ后都分别增加了一个SPP模块来采样表示性点,采样过程如图4. 使用了几个池化层,然后池化结果flatten并concatenate起来作为下层的输入。这里四个池化层的宽度和高度都一样,大小为{1,3,6,8},所以总共有S=1+3×3+6×6+8×8=110个anchor点。(两个分支的SPP模块都一样,因为要保证这两个分支的维度一样)
这里SPP提供了足够的全局统计数据来弥补通道降维可能导致的性能下降。假设输入特征图宽和高都96,则N=W×H,总共节约计算为96×96/110=84倍!
Asymmetric Fusion Non-local Block
通常的特征融合都是addition/concatenation,是以pixel-wise和局部的方式执行的,而这里借助了APNB的非对称性,通过APNB来融合多level的特征来捕获long range dependencies,这个模块叫做Fusion Non-local Block.
FNB有两个输入:一个是high -level的特征图 X h ∈ R C h × N h X_h \in R^{C_h×N_h} Xh∈RCh×Nh,还有一个是low-level 的特征图 X l ∈ R C l × N l X_l \in R^{C_l×N_l} Xl∈RCl×Nl, N h , N l N_h,N_l Nh,Nl分别是 X h , X l X_h,X_l Xh,Xl的空间位置数量, C h , C l C_h,C_l Ch,Cl则分别是通道数,这里首先对他们使用一个1×1卷积降维到相同的通道 C ^ \hat{C} C^,得到两个embedding ε h ∈ R C ^ × N h 和 ε l ∈ R C ^ × N l \varepsilon_h ∈ R^{\hat{C}×N_h} 和\varepsilon_l ∈ R^{\hat{C}×N_l} εh∈RC^×Nh和εl∈RC^×Nl。然后他们相乘得到相似性矩阵 V F = ε h T × ε l . V_F = \varepsilon^ T_ h × \varepsilon _l . VF=εhT×εl. V F ∈ R N h × N l V_F \in R^{N_h×N_l} VF∈RNh×Nl,然后对 V F V_F VF运用正则化,然后再和前面一样聚集所有位置对他们的影响 O F = V F → × ε l T O_F= \mathop{V_F}\limits ^{\rightarrow}×\varepsilon ^T_l OF=VF→×εlT,输出的注意力 O F ∈ R N h × C ^ O_F ∈ R^{N_h×\hat{C}} OF∈RNh×C^,表示的是 ε l \varepsilon_l εl对 ε h \varepsilon _h εh的奖励,是从 ε l \varepsilon_l εl精心选择的。之后 O F O_F OF送入1×1卷积恢复通道 C h C_h Ch。于是得到的输出如下:
Y F = c a t ( W 0 ( O F T ) , X h ) . Y_F=cat(W_0(O_F^T),X_h). YF=cat(W0(OFT),Xh).
整个流程可以见图3. AFNB继承自APNB。
Experiments
本人非学习语义分割的,所以只关注其对Non-local的改进,更多的实验信息请见论文。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Tngr3tMm-1624886546505)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/2f49eb78-7370-4c6e-8acf-b2f56c2f7738/Untitled.png)]](/image/aHR0cHM6Ly9pbWctYmxvZy5jc2RuaW1nLmNuLzIwMjEwNjI4MjEyMzI2NjMucG5n)
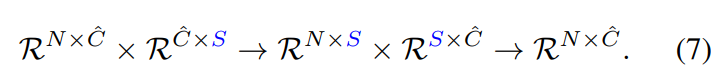
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wmbQ3NvL-1624886546511)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/a7b4981a-be3a-49dd-8e78-49ef55992e55/Untitled.png)]](/image/aHR0cHM6Ly9pbWctYmxvZy5jc2RuaW1nLmNuLzIwMjEwNjI4MjEyNTQ3NTIxLnBuZz94LW9zcy1wcm9jZXNzPWltYWdlL3dhdGVybWFyayx0eXBlX1ptRnVaM3BvWlc1bmFHVnBkR2ssc2hhZG93XzEwLHRleHRfYUhSMGNITTZMeTlpYkc5bkxtTnpaRzR1Ym1WMEwzbGhibWRvWVc4eU1ERTJNRGN3TXpBeE1ERT0sc2l6ZV8xNixjb2xvcl9GRkZGRkYsdF83MA%3D%3D)