定义
递归是一种在程序设计中常用的技术,它允许一个函数调用自身来解决问题。递归通常用于解决那些可以被分解为相似的子问题的问题,这些问题的解决方式具有自相似性。在数据结构和算法中,递归是一种重要的解决问题的方法,尤其是在处理树形结构和图结构时。
递归的基本概念
递归函数:一个函数直接或间接地调用自身。
基线条件:递归必须有一个或多个基线条件,以防止无限递归。基线条件通常是递归终止的简单情况。
递归步骤:递归函数调用自身时,每次调用都应该使问题更接近基线条件。
递归的工作原理
问题分解:将问题分解为更小的子问题。
递归调用:对每个子问题,递归函数调用自身。
合并结果:将子问题的解合并以形成原始问题的解。
基线条件:当问题规模足够小,可以直接解决时,停止递归。
简单例子
1. 阶乘计算
阶乘函数是一个经典的递归示例:
def factorial(n):
if n == 0: # 基线条件
return 1
else:
return n * factorial(n-1) # 递归调用2. 斐波那契数列
斐波那契数列是另一个递归示例,其中每个数是前两个数的和:
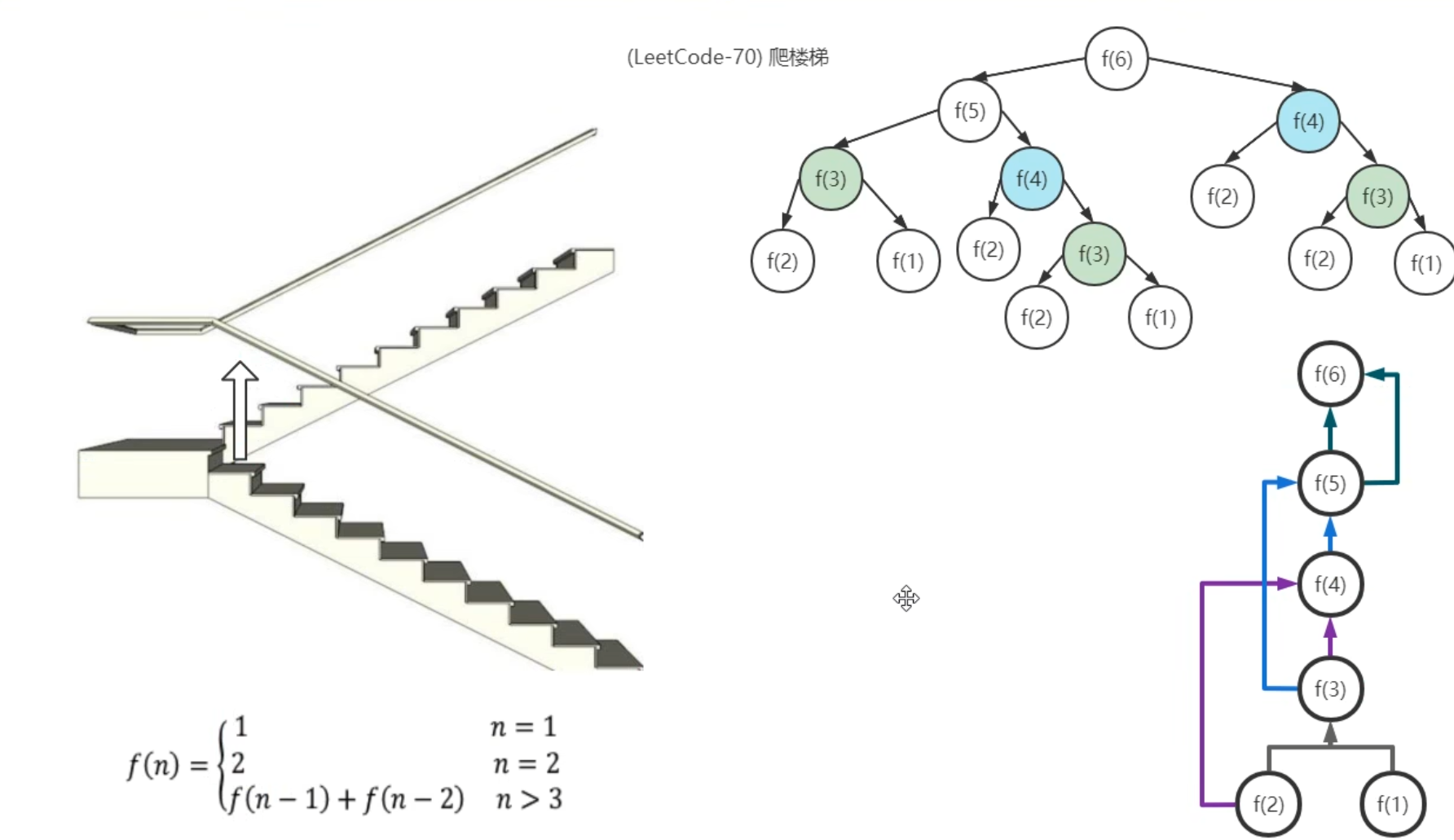
题目:
思路:我们用 f(x) 表示爬到第 x 级台阶的方案数,考虑最后一步可能跨了一级台阶,也可能跨了两级台阶,所以我们可以列出如下式子:
f(x)=f(x−1)+f(x−2)
它意味着爬到第 x 级台阶的方案数是爬到第 x−1 级台阶的方案数和爬到第 x−2 级台阶的方案数的和。很好理解,因为每次只能爬 1 级或 2 级,所以 f(x) 只能从 f(x−1) 和 f(x−2) 转移过来,而这里要统计方案总数,我们就需要对这两项的贡献求和。
c代码实现:
int F(int n)
{
if(n<=2)
return n;
else
return F(n-1)+F(n-2);
}python实现:
def F(n):
if n <= 2:
return n
else:
return F(n - 1) + F(n - 2)java 实现:
public class Fibonacci {
public static int F(int n) {
if (n <= 2) {
return n;
} else {
return F(n - 1) + F(n - 2);
}
}
public static void main(String[] args) {
// 测试函数
int number = 10; // 例如,计算第10个斐波那契数
System.out.println("Fibonacci of " + number + " is " + F(number));
}
}js实现:
function F(n) {
if (n <= 2) {
return n;
} else {
return F(n - 1) + F(n - 2);
}
}关于此题的其他几个解法后续出!
知识星球:
https://articles.zsxq.com/id_xsfrtk2w9wp6.html