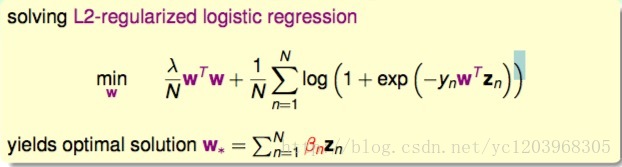机器学习技法-Kernel Logistic Regression

大纲

这里写图片描述

上节课我们主要介绍了Soft-Margin SVM，即如果允许有分类错误的点存在，那么在原来的Hard-Margin SVM中添加新的惩罚因子C，修正原来的公式，得到新的 $\alpha_n$ 值。最终的到的 $\alpha_n$ 有个上界，上界就是C。Soft-Margin SVM权衡了large-margin和error point之前的关系，目的是在尽可能犯更少错误的前提下，得到最大分类边界。本节课将把Soft-Margin SVM和我们之前介绍的Logistic Regression联系起来，研究如何使用kernel技巧来解决更多的问题。

Soft-Margin SVM as Regularized Model

1 Slack Variables $\xi_n$

这里写图片描述

对于任意的 $(b,w)$ , $\xi_n$ 描述的是 $(x_n,y_n)$ 距离 $y_n(w^Tz_n+b)=1$ 的边界有多远。

violation margin,即 $(x_n,y_n)$ 不满足 $y_n(w^Tz_n+b)\ge1$ , $\xi_n=1-y_n(w^Tz_n+b)>0$
not violation margin,即 $(x_n,y_n)$ 满足 $y_n(w^Tz_n+b)\ge1$ , $\xi_n=0$

所以我们可以把两种情况统一起来，得到一种无约束的形式的soft-margin SVM

min b, w 1 2 w T w + C \sum n = 1 N m a x (1 - y n (w T z n + b), 0)

$\min_{b,w} \frac{1}{2}w^Tw+C\sum_{n=1}^Nmax(1-y_n(w^Tz_n+b),0)$

2 Unconstrained Form

这里写图片描述

我们可以把 $max(1-y_n(w^Tz_n+b),0)$ 当成一种 $\hat{err}$ ,那么我们可以整理为

min 1 2 w T w + C \sum e r r^

$\min \frac{1}{2}w^Tw+C\sum\hat{err}$
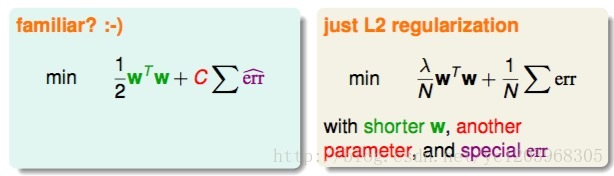
这个和我们以前学过的L2 regularization的形式有点类似

min λ N w T w + 1 N \sum e r r

$\min \frac{\lambda}{N}w^Tw+\frac{1}{N}\sum err$
既然unconstrained form SVM与L2 Regularization的形式是一致的，而且L2 Regularization的解法我们之前也介绍过，那么为什么不直接利用这种方法来解决unconstrained form SVM的问题呢？

这种unconstrained form SVM的形式不是QP问题，对偶问题和核技巧都没有用
还有 $max(\cdot,0)$ 是不可导的，导致这个最优化问题很难被优化

3 SVM as Regularized Model

这里写图片描述

我们可以把SVM看做一种正则化模型，Soft-Margin SVM中的large margin对应着L2 Regularization中的short w，也就是都让hyperplanes更简单一些。Regularization中的 $\lambda$ 和Soft-Margin SVM中的C是互相对应的，C越大对应于 $\lambda$ 减小，所得到的超平面就越复杂。反之，所得到的超平面就越复杂。Large-Margin等同于Regularization，都起到了防止过拟合的作用。

建立了Regularization和Soft-Margin SVM的关系，接下来我们将尝试看看是否能把SVM作为一个regularized的模型进行扩展，来解决其它一些问题。

SVM versus Logistic Regression

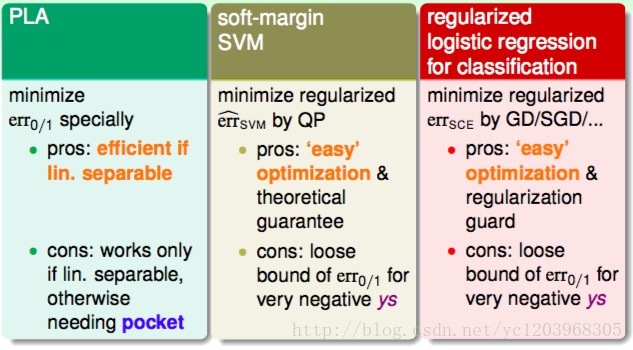
1 Algorithmic Error Measure of SVM

这里写图片描述

我们把SVM 的error函数画出来，如上图所示，我们称之为hinge error measure.它是0/1误差的凸的上界。因为 $err_{SVM}$ 是一个是一个凸函数，使它在最佳化问题中有更好的性质，我们可以通过优化 $err_{SVM}$ 来优化 $err_{0/1}$ .

2 Connection between SVM and Logistic Regression

这里写图片描述
我们接着把Logistics Regression的 error function画出来。我们发现 $err_{SCE}$ 和 $err_{SVM}$ 是近似的。因为当ys趋向正无穷大的时候， $err_{SCE}$ 和 $err_{SVM}$ 都趋向于零；当ys趋向负无穷大的时候， $err_{SCE}$ 和 $err_{SVM}$ 都趋向于正无穷大。正因为二者的这种相似性，我们可以把SVM看成是L2-regularized logistic regression。

3 Linear Models for Binary Classification

这里写图片描述

我们说正则化的logistic regression可以近似看做SVM，那么如果我们求解了一个SVM问题，那么SVM问题的解能否为logistic regression所用呢？

SVM for Soft Binary Classification

1 SVM for Soft Binary Classification

这里写图片描述
我们有两种Naive的思路

第一种思路是先得到SVM的解 $(b_{svm},w_{svm})$ ，然后直接代入到logistic regression中，得到 $g(x)=θ(w^T_{svm}x+b_{svm})$ 。这种方法直接使用了SVM和logistic regression的相似性，一般情况下表现还不错。但是，这种形式过于简单，与logistic regression的关联不大，没有使用到logistic regression中好的性质和方法。
第二种思路是同样先得到SVM的解 $(b_{svm},w_{svm})$ ，然后把 $(b_{svm},w_{svm})$ 作为logistic regression的初始值，再进行迭代训练修正，速度比较快，最后，将得到的b和w代入到g(x)中。这种做法有点显得多此一举，因为并没有比直接使用logistic regression快捷多少。

下面我们介绍一种方法，可以融合两种算法的优势

2 A Possible Model: Two-Level Learning

我们构造以下函数

g (x) = θ (A \cdot (w T s v m ϕ (x) + b s v m) + B)

$g(x) = \theta(A \cdot (w^T_{svm}\phi(x)+b_{svm})+B)$
这个函数有两点优势

我们可以先得到SVM的解，这里可以利用核技巧。利用了SVM的优点
然后再用通用的logistic regression优化算法，通过迭代优化，得到最终的A和B。

一般缩放系数A>0,如果w_{SVM}相对来说不错，B $\approx 0$ ,如果 $b_{SVM}$ 相对来说不错

接下来我们就可以构造极大似然函数

这里写图片描述

这是一个只含有两个参数的最小化问题，我么可以利用GD/SGD.或者更好的方法求解。
我们称这个算法是Probabilistic SVM。下面我们总结一下算法思路

3 Probabilistic SVM

这里写图片描述

一般来说Probabilistic SVM的决策边界和SVM的决策边界不一致。

最后我们可以这样理解Kernel SVM,可以把Kernel SVM近似当做在Z空间中做logistics regression。

接下来我们介绍一种在Z空间中做logistics regression的精确方法。

Kernel Logistic Regression

1 Key behind Kernel Trick

首先我们回顾一下Kernel Trick的关键的地方，就是 $w^*$ 可以表示为

w * = \sum n = 1 N β n z n

$w^* = \sum_{n=1}^N\beta_nz_n$
然后，我们就可以引入核函数

w T * z = \sum n = 1 N β n z T n z = \sum n = 1 N K (x n, x)

$w_*^Tz = \sum_{n=1}^N\beta_nz_n^Tz = \sum_{n=1}^NK(x_n,x)$

我们之前介绍过SVM、PLA包扩logistic regression都可以表示成z的线性组合，这也提供了一种可能，就是将kernel应用到这些问题中去，简化z空间的计算难度。

这里写图片描述

2 Representer Theorem

首先我们介绍一下表示定理

对于L2-regularized linear model，如果它的最小化问题形式为如下的话，那么最优解 $w_∗=\sum^N_{n=1}\beta_nz_n$ 。

这里写图片描述

下面给出简单证明

这里写图片描述

至此，我们知道了所有的L2 regularized linear 都可以核化

3 Kernel Logistic Regression

下面我们尝试用核技巧来求解Logistic Regression

首先我们回顾一下以前的L2-regularized logistic regression 问题

这里写图片描述

因为表示定理的存在，即 $w_∗=\sum^N_{n=1} \beta_n z_n$ .不失最优性，我们可以求解最优的 $\beta$ ,而不是w

这里写图片描述

上式中，所有的w项都换成 $\beta_n$ 来表示了，变成了没有条件限制的最优化问题。我们把这种问题称为kernel logistic regression，即引入kernel，将求w的问题转换为求 $\beta_n$ 的问题。上面那个问题可以通过一般的无约束优化算法求解

4 Kernel Logistic Regression (KLR) : Another View

我们可以从另外一个角度来看待Kernel Logistic Regression

这里写图片描述

上式中log项里的 $\sum^N_{m=1}\beta_mK(x_m,x_n)$ 可以看成是变量 $\beta$ 和 $K(x_m,x_n)$ 的内积。上式第一项中的 $\sum^N_{n=1}\sum^N_{m=1} \beta_n\beta_mK(x_n,x_m)$ 可以看成是关于 $\beta$ 的正则化项 $\beta^TK\beta$ 。所以，KLR是 $\beta$ 的线性组合，其中包含了kernel内积项和kernel regularizer。这与SVM是相似的形式。

如果我们把KLR当做是关于 $\beta$ 的线性模型，那么我们实际上是将样本X转换到了一个维度为N的Z空间

如果我们把KLR当做是关于 $w$ 的线性模型，那么我们实际是将样本X转换到了一个维度为 $\hat{d}$ 的Z空间

最后值得注意的是，KLR中的系数 $\beta$ 通常都很密集，就是大部分不为0，而SVM中的系数 $\alpha$ 通常都很稀疏，就是大部分都为0.