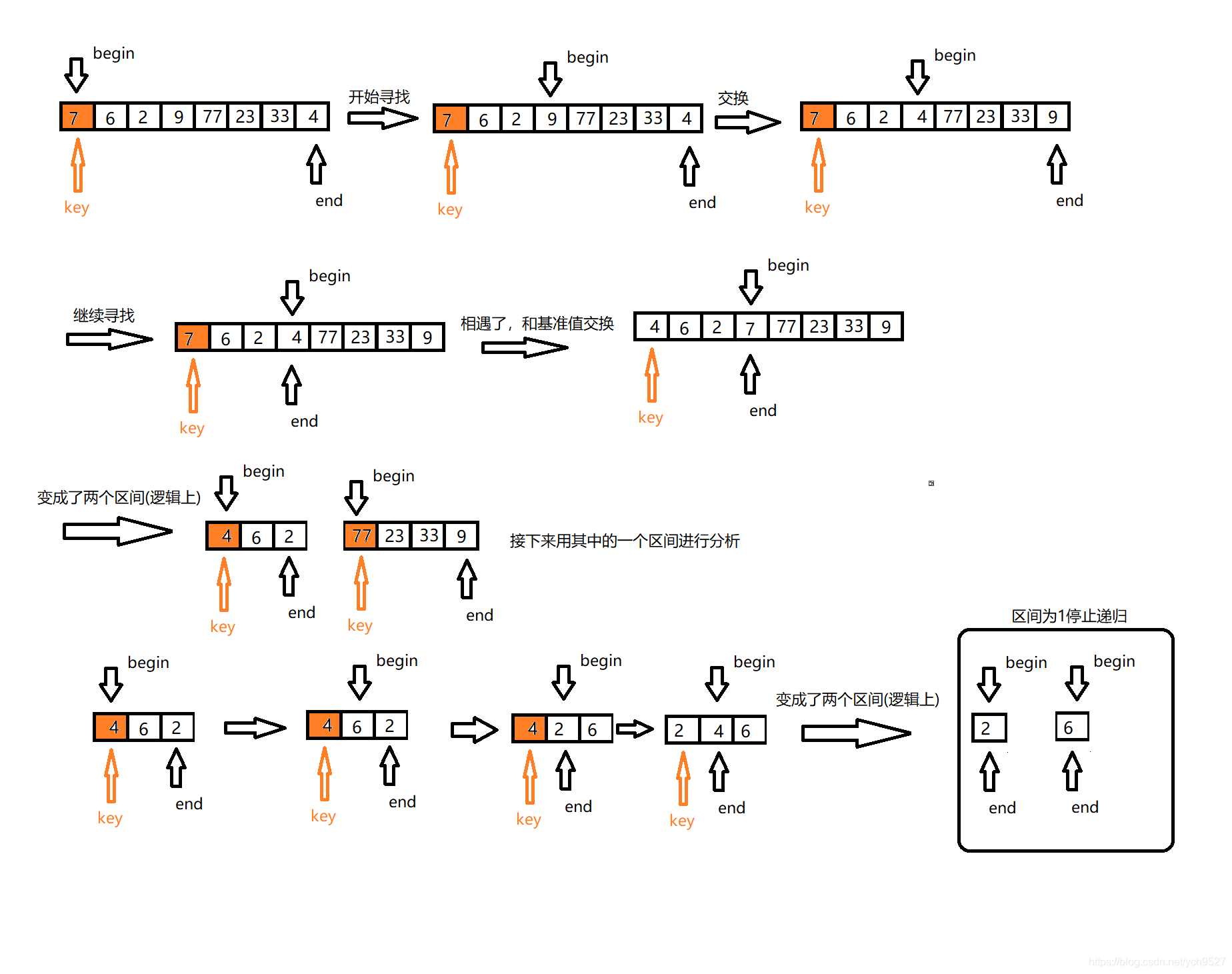
1.hoare(左右指针)法

1.给定一个基准值

2.待划分的区间从后往前寻找比基准值小的值

3.待划分区间从前往后寻找比基准值大的值

4.交换2.3步找到的数据，再循环执行2.3步

5.2和3的查找位置如果相遇则停止循环，相遇位置的值和基准值进行交换

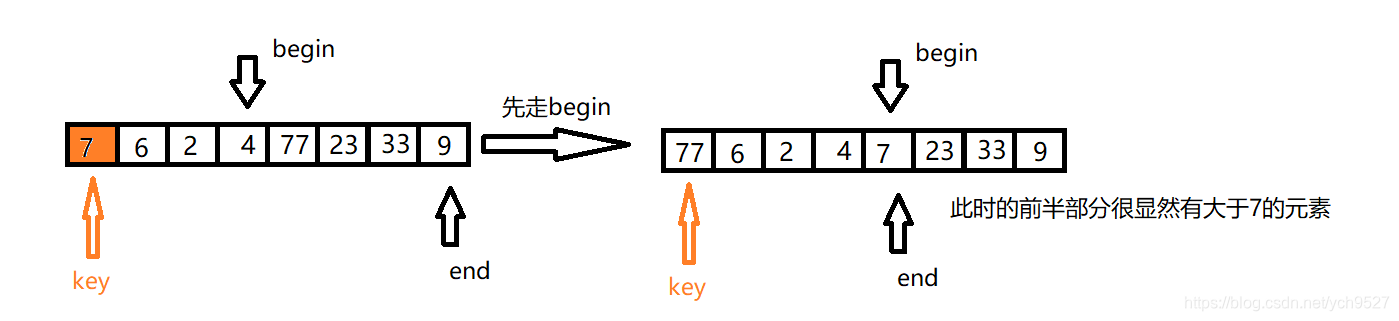
特别注意： 第二步和第三步的顺序不能够颠倒，因为当进行了一次交换之后，begin对应的值是小于基准值的，而end对应的值是大于基准值的，当没有满足条件的时候，相遇位置在end处会导致将比基准值大的数据换到前面去；

实现代码：

int partion(int *arr, int begin,int end)//hoare
{
	int key = begin;
	while (begin<end)
	{
		while (begin<end&&arr[key] <= arr[end] )//从后往前寻找比key小的值
		{
			end--;
		}
		while (begin<end&&arr[begin] <= arr[key])//从前往后寻找比key大的值
		{
			begin++;
		}
		if (begin < end)
			Swap(&arr[begin], &arr[end]);
	}
	Swap(&arr[begin], &arr[key]);//相遇位置的值和key进行交换
	return begin;//返回相遇位置
}

void QuickSort(int *arr, int begin, int end)
{
	if (begin >= end)
		return;
	 int keypos = partion(arr, begin, end);

	 QuickSort(arr, begin, keypos - 1);//前段
	 QuickSort(arr, keypos + 1, end);//后段

}

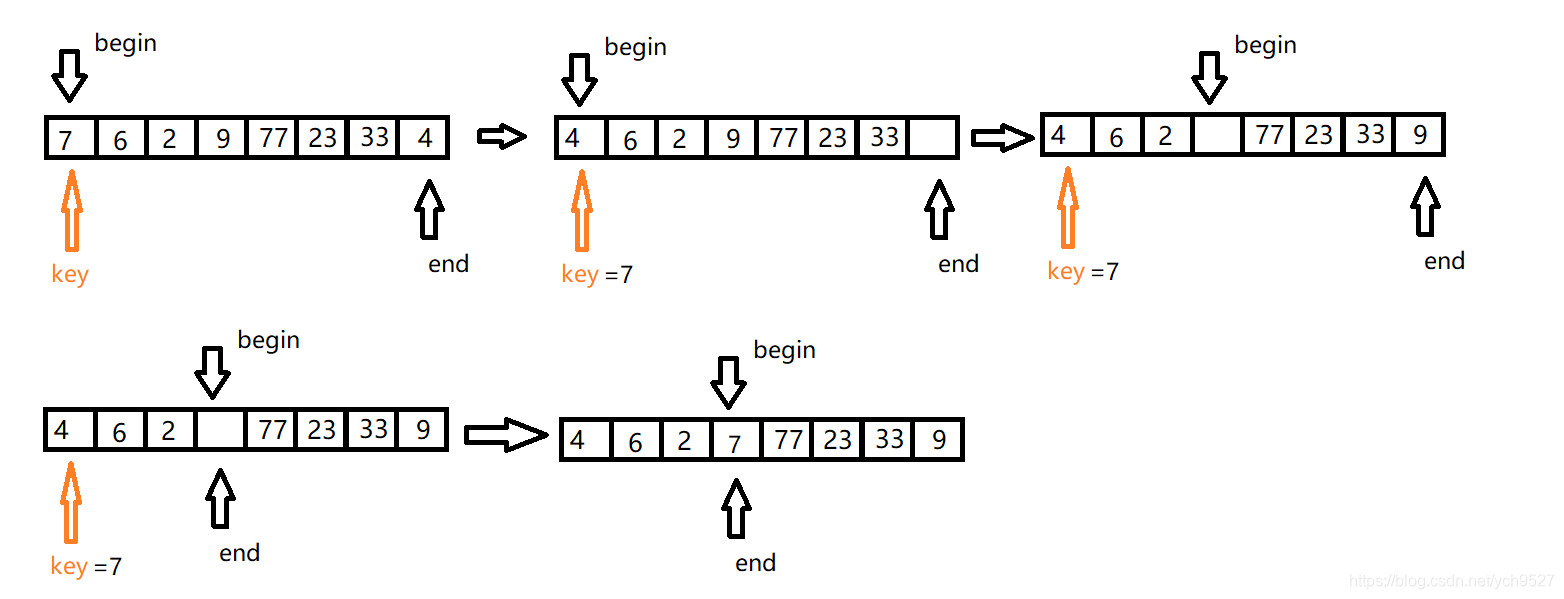
2.挖坑法

1.选取基准值，基准值处为坑

2.从后往前寻找比基准值小的值填入坑内

3.从前往后寻找比基准值大的填入第二步的坑内

4.循环执行2和3，直至相遇再退出循环

5.将基准值填入相遇位置的坑内

第二步和第三步同样不能颠倒顺序，如果颠倒了位置，begin先走，然后找到对应的值，直接将end处的值给覆盖了

实现代码：

int partion2(int *arr, int begin, int end)//挖坑
{
	int key = arr[begin];
	while (begin<end)
	{
		while (begin<end&&key <= arr[end])//从后往前寻找比key小的值
		{
			end--;
		}
		arr[begin] = arr[end];//将比key小的值填入坑内

		while (begin<end&&arr[begin] <= key)//从前往后寻找比key大的值
		{
			begin++;
		}
		arr[end] = arr[begin];//比key大的值填入坑内
	}
	arr[begin] = key;//基准值填入相遇位置
	return begin;//返回相遇位置
}
void QuickSort(int *arr, int begin, int end)
{
	if (begin >= end)
		return;
	 int keypos = partion2(arr, begin, end);

	 QuickSort(arr, begin, keypos - 1);//前段
	 QuickSort(arr, keypos + 1, end);//后段

}

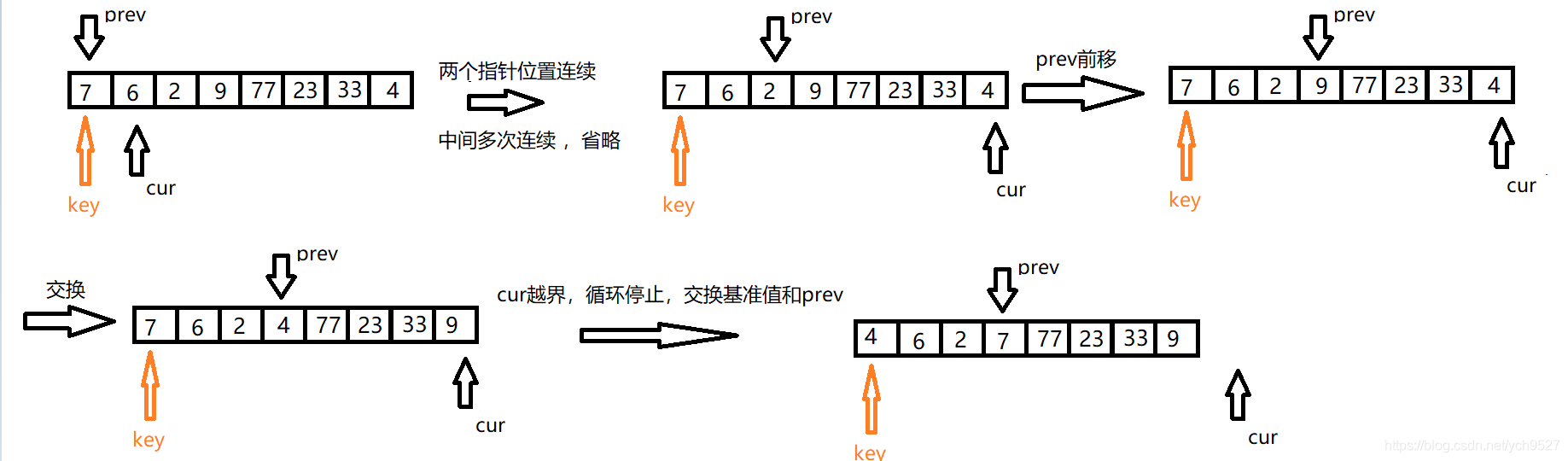
3.前后指针法

1.选取基准值

2.建立两个指针，prev指向最后一个小于基准值的元素，cur指向下一个小于基准值的位置

3.当prev和cur不连续时，代表两个指针之间有大于基准值的元素，先让prev往后挪动一个位置，再和cur进行交换； 如果连续，则代表两者之间没有大于基准值的元素；

4.当cur大于等于数组长度即越界时，停止循环，此时最后一个小于基准值的数据和基准值进行交换；

实现代码：

int partion3(int *arr, int begin, int end)//前后指针
{
	int key = arr[begin];	
	int prev = begin;//最后一个小于基准值的位置
	int cur = prev + 1;//当前位置
	while (cur<=end)
	{
		if (arr[cur]<key&&++prev!= cur)//找到下一个小于基准值的位置且两个指针位置不连续
		{
			Swap(&arr[prev], &arr[cur]);//进行交换
		}
		cur++;
	}
	Swap(&arr[begin], &arr[prev]);//基准值与最后一个小于基准值的值进行交换

	return prev;
}

void QuickSort(int *arr, int begin, int end)
{
	if (begin >= end)
		return;
	 int keypos = partion3(arr, begin, end);

	 QuickSort(arr, begin, keypos - 1);//前段
	 QuickSort(arr, keypos + 1, end);//后段

}

4.特性

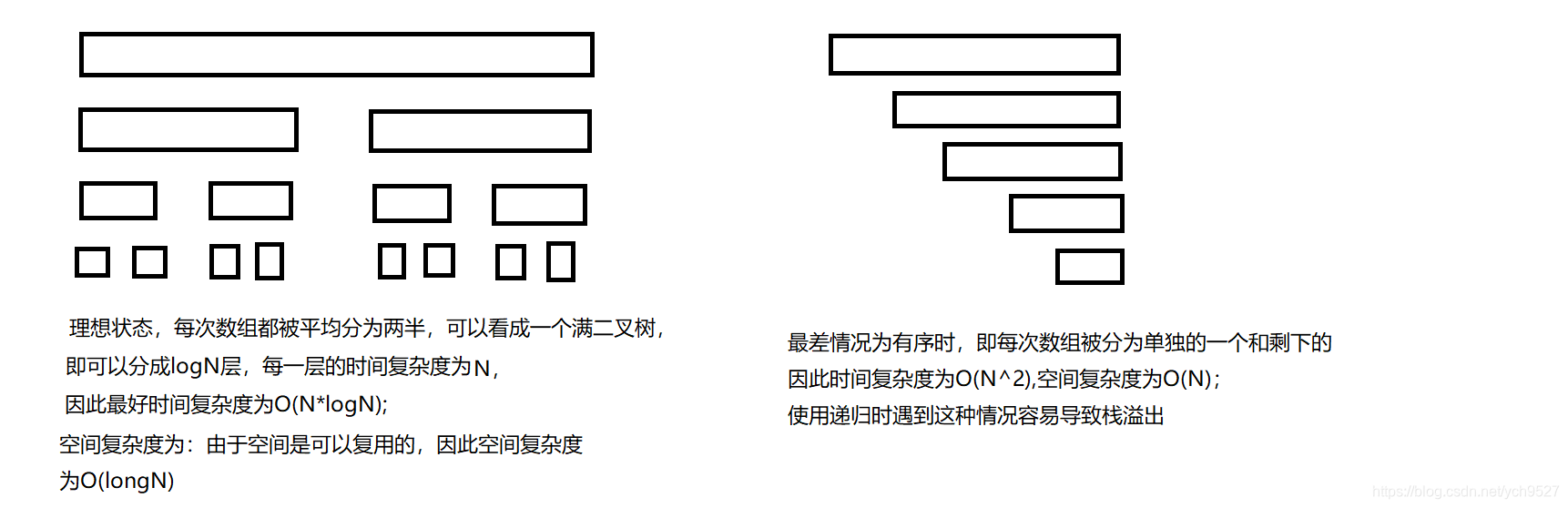
1.时间复杂度和空间复杂度

2.稳定性：由于快排会进行交换，因此不具备稳定性

3.敏感度：有序和无序的差别很大，数据敏感度为敏感

5.优化版本

5.1 优化一

由上述特性分析我们知道，当数组元素有序时快排的时间复杂度会非常的高，这是由于基准值一直是当前序列第一个元素的原因，因此我们可以对其进行优化，即改变基准值的选取，下面以haore为例；

我们可以通过，选取前中后三个下标对应的3个元素中的居中值来充当基准值，这样一来最坏的情况便变成了最好的情况了，实现代码如下；

实现代码：

int Getmid(int *arr,int begin,int end )//三数取中
{
	int mid = begin + (end - begin) / 2;
	if (arr[begin] < arr[mid])
	{
		if (arr[mid] < arr[end])
			return mid;
		else
		{
			if (arr[begin] < arr[end])
			{
				return end;
			}
			else
			{
				return begin;
			}
		}
	}
	else
	{
		if (arr[end] < arr[mid])
		{
			return mid;
		}
		else
		{
			if (arr[end] < arr[begin])
			{
				return end;
			}
			else
			{
				return begin;
			}
		}
	}
}

int partion(int *arr, int begin,int end)//hoare
{
	int key = Getmid(arr, begin, end);//三数取中
	Swap(&arr[begin], &arr[key]);
	key = begin;


	while (begin<end)
	{
		while (begin<end&&arr[key] <= arr[end] )//从后往前寻找比key小的值
		{
			end--;
		}
		while (begin<end&&arr[begin] <= arr[key])//从后往前寻找比key大的值
		{
			begin++;
		}
		if (begin < end)
			Swap(&arr[begin], &arr[end]);
	}
	Swap(&arr[begin], &arr[key]);//相遇位置的值和key进行交换
	return begin;//返回相遇位置
void QuickSort(int *arr, int begin, int end)
{
	if (begin >= end)
		return;

	int keypos = partion(arr, begin, end);

	QuickSort(arr, begin, keypos - 1);//前段
	QuickSort(arr, keypos + 1, end);//后段

}
}

5.2 优化二

由上述分析可以知道，快速排序在数组元素个数非常多的时候的计算速度是非常快的，如果元素个数较少的话计算起来就比较复杂了，因此我们可以进行判定，在数组元素较少时采用其他的排序方式，一般采用直接插入排序；

实现代码

void QuickSort(int *arr, int begin, int end)
{
	if (begin >= end)
		return;

	if ((end - begin + 1) > 10)
	{
		int keypos = partion3(arr, begin, end);

		QuickSort(arr, begin, keypos - 1);//前段
		QuickSort(arr, keypos + 1, end);//后段
	}
	else
	{
		InsertSort(arr+begin, end-begin+1);//元素个数小于10采用直接插入排序,有序程度越高插入排序时间复杂度越小
	}

}

6.利用栈和队列非递归实现快排

递归改非递归的方法：
1.改循环(斐波那契数列递归改迭代)
2.栈模拟存储数据非递归

非递归和递归方式进行比较：
1.提高效率(递归建立栈桢是有消耗的，但是对于现代计算机，这种消耗对整体的影响微乎其微)
2.递归的最大缺陷是，如果栈桢的深度太深容易发生栈溢出。因为系统栈的空间一般不大，都在M级别。
如果用数据结构的栈和队列来模拟实现的话就可以很好的解决溢出问题，这是因为此时数据是存储在堆上的，堆的空间是G级别的

6.1利用栈实现

栈的特性是先进后出，因此可以先完成左半部分的排序，再完成右半部分的排序；

实现代码：

void QuickSortNoRSt(int *arr, int begin,int end)//非递归,利用栈
{
	stack st;
	StackInit(&st);
	if (end-begin)
	{
		//入栈
		StackPush(&st, end);
		StackPush(&st, begin);
	}
	while (!StackEmpty(&st))
	{
		int begin = StackTop(&st);//出栈
		StackPop(&st);
		int end = StackTop(&st);
		StackPop(&st);

		int keypos=partion(arr, begin, end);

		//入栈
		if (keypos+1 < end)
		{
			StackPush(&st, end);
			StackPush(&st, keypos+1);
		}
		if (keypos - 1 > begin)
		{
			StackPush(&st, keypos - 1);
			StackPush(&st, begin);
		}
	}
	StackDestory(&st);
}

6.2利用队列实现

队列的特性是先进先出，我们可以一层一层的实现排序；

实现代码：

void QuickSortNoRQe(int *arr, int begin, int end)//利用队列实现快排
{
	Queue q;
	QueueInit(&q);
	if (end - begin)
	{
		//入队
		QueuePush(&q, begin);
		QueuePush(&q, end);
	}
	while (!QueueEmpty(&q))
	{
		//出队
		int begin = QueueFront(&q);
		QueuePop(&q);
		int end = QueueFront(&q);
		QueuePop(&q);

		int keypos = partion2(arr, begin, end);

		//子序列入队
		if (begin<keypos-1)
		{
			QueuePush(&q, begin);
			QueuePush(&q, keypos - 1);
		}
		if (keypos + 1 < end)
		{
			QueuePush(&q, keypos + 1);
			QueuePush(&q, end);
		}
	}
	QueueDestory(&q);
}

性能分析：
非递归的方式实现快排，时间复杂度依旧是O(N*logN)，空间复杂度为O(logN)；