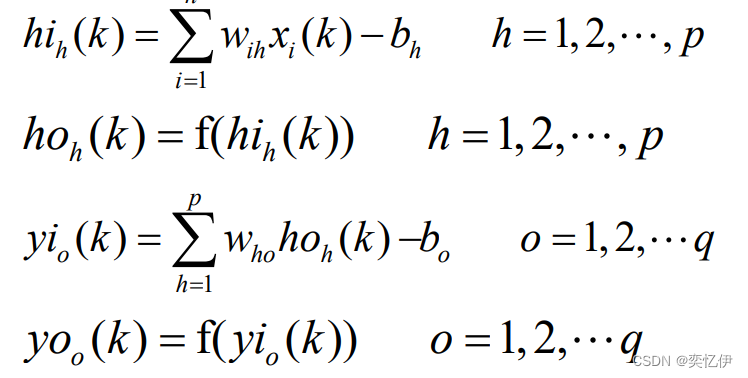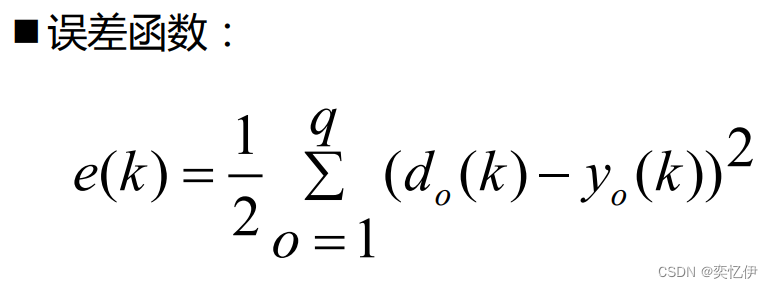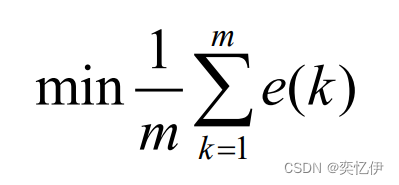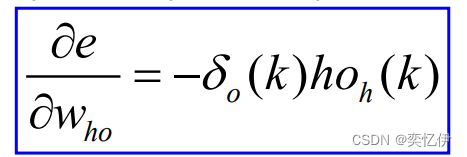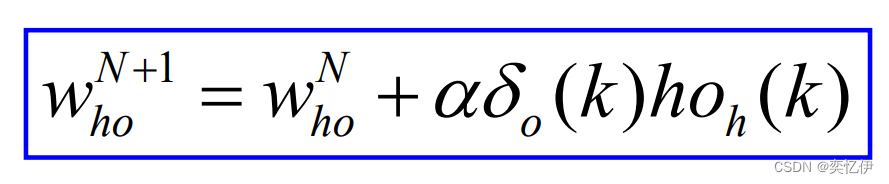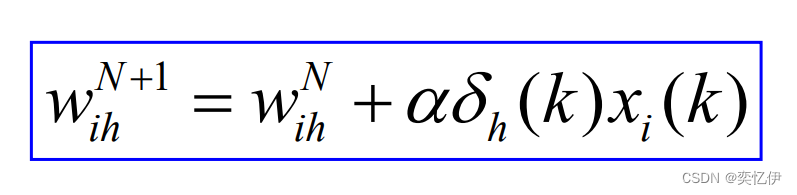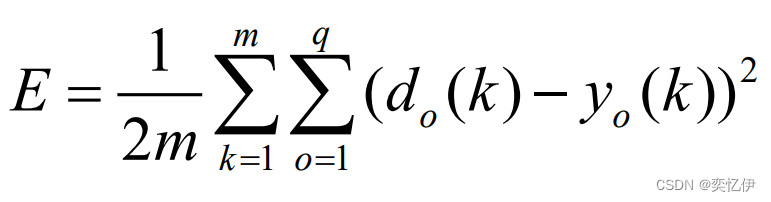BP神经网络的学习记录
目录
一·人工神经网络
(一)发展历程
神经元模型(MP模型)和 感知机(Perceptron)--- 低潮 --- → 误差反向传播法(BP法)
--- 低潮(冰河期)--- → 多层神经网络
(二)定义
人工神经网络是对人脑神经网络的抽象和模拟,以大量相同结构的简单单元进行连接。
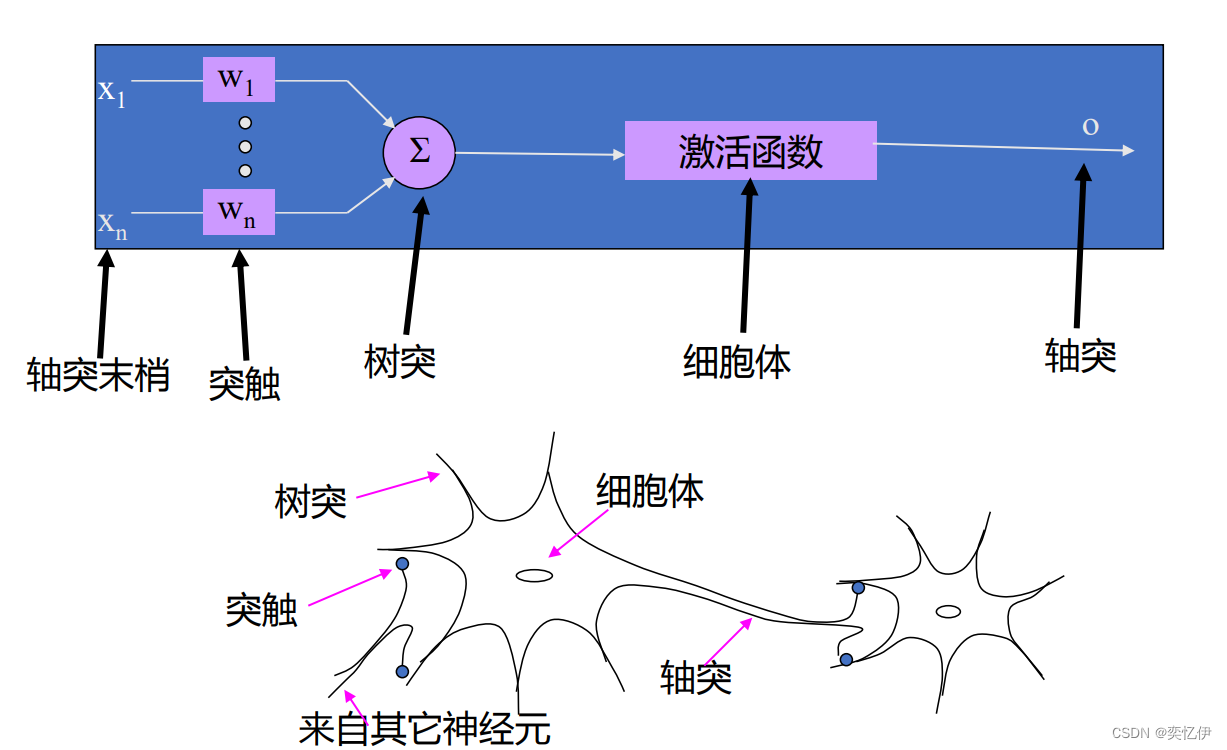
从生物神经元抽象出人工神经元模型
(三)人工神经元
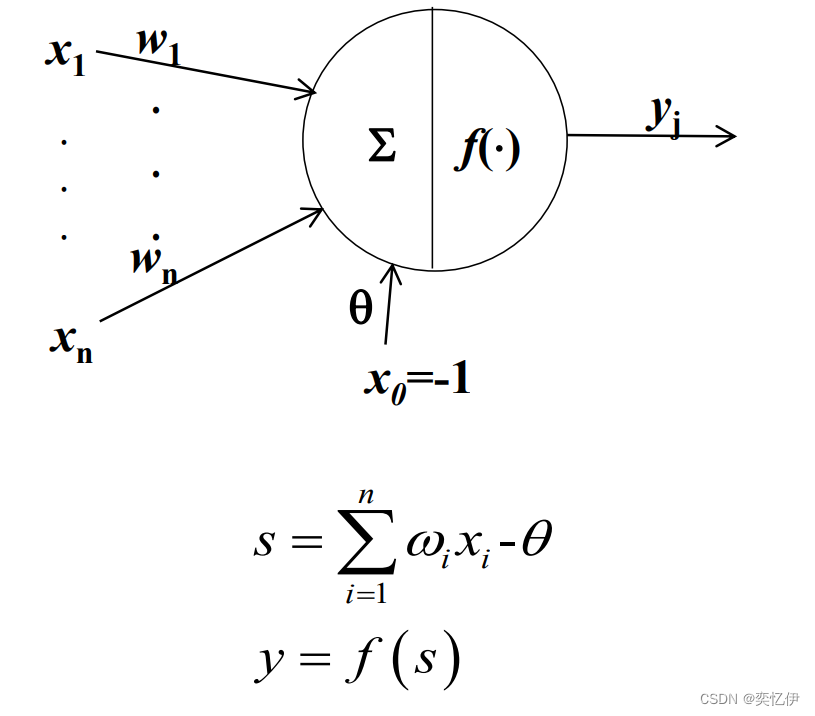
1.单层感知机
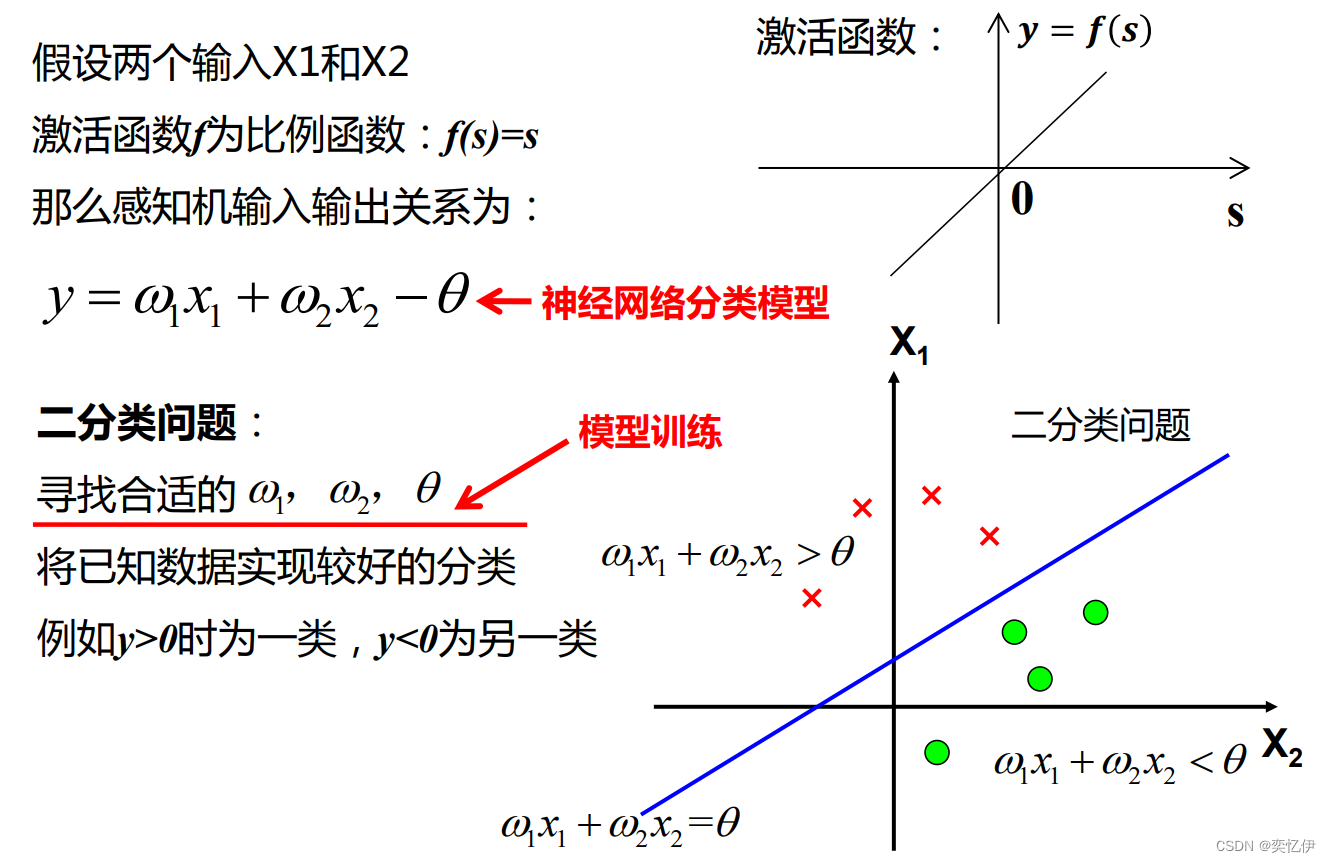
只有一个神经元且激活函数为线性函数。
单层感知机可以解决简单的二分类问题,当输入输出不是线性关系时,单层感知机就不起作用了
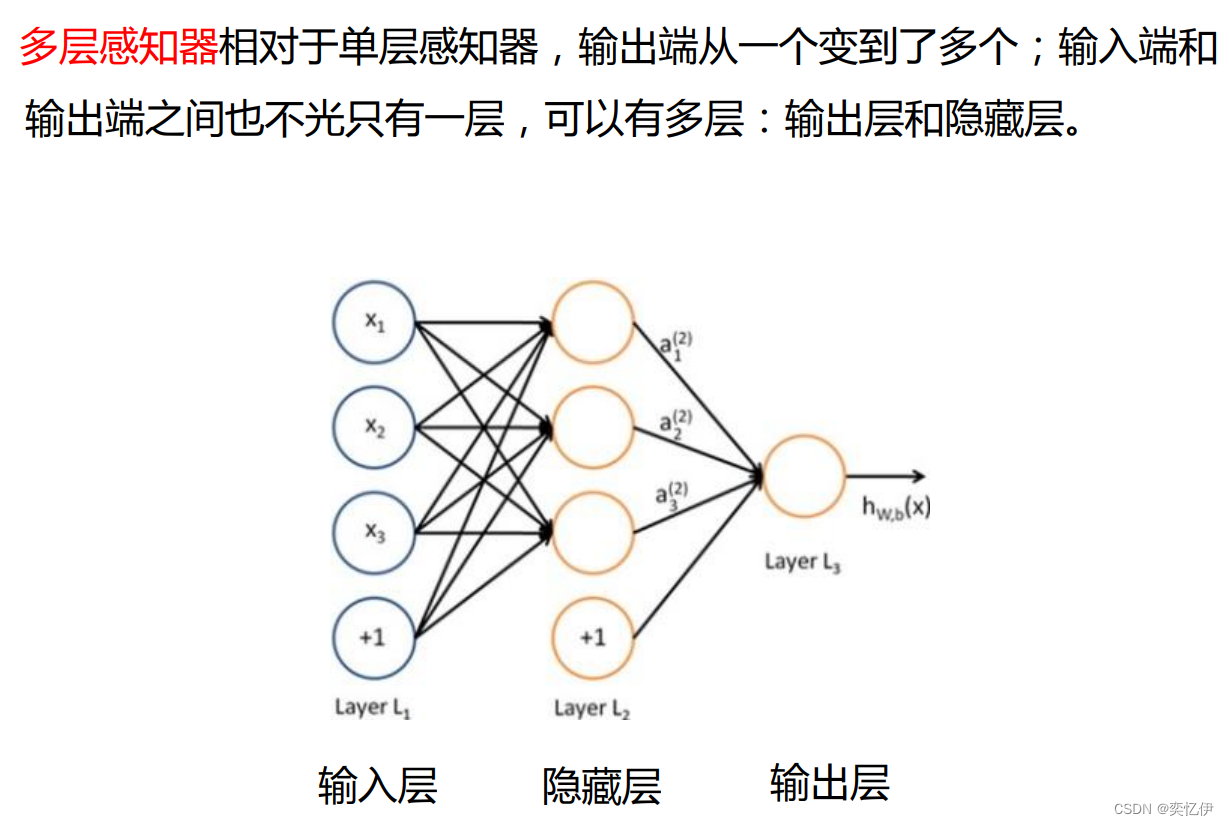
2.多层感知机
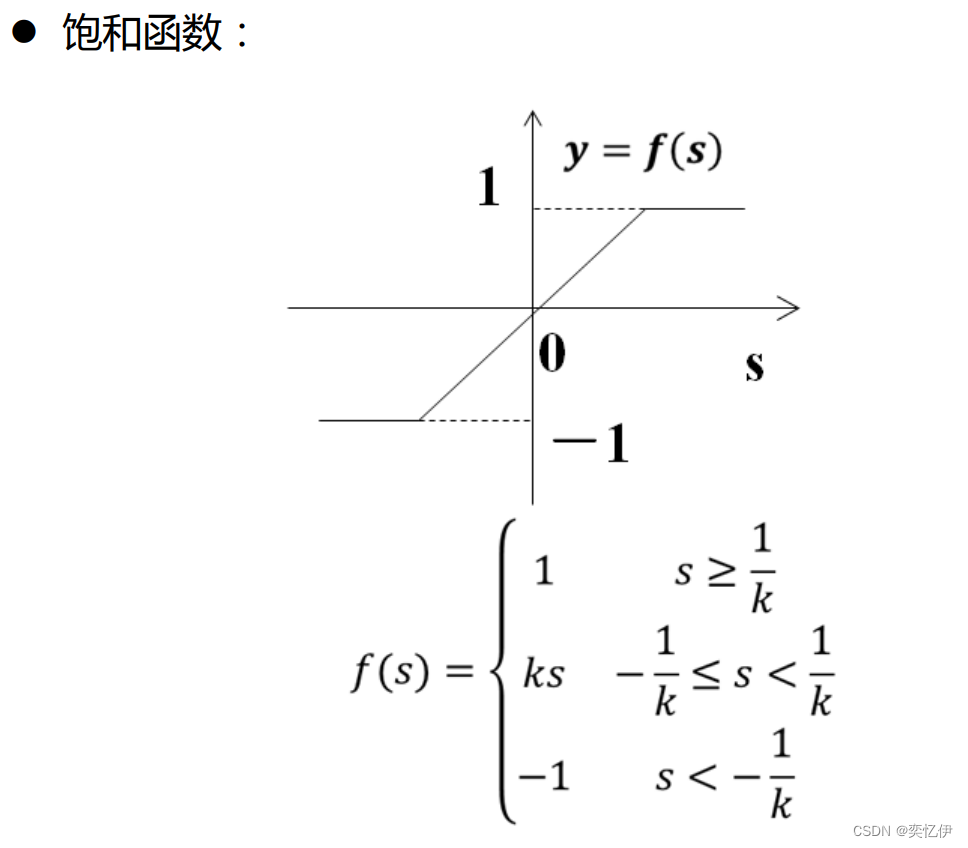
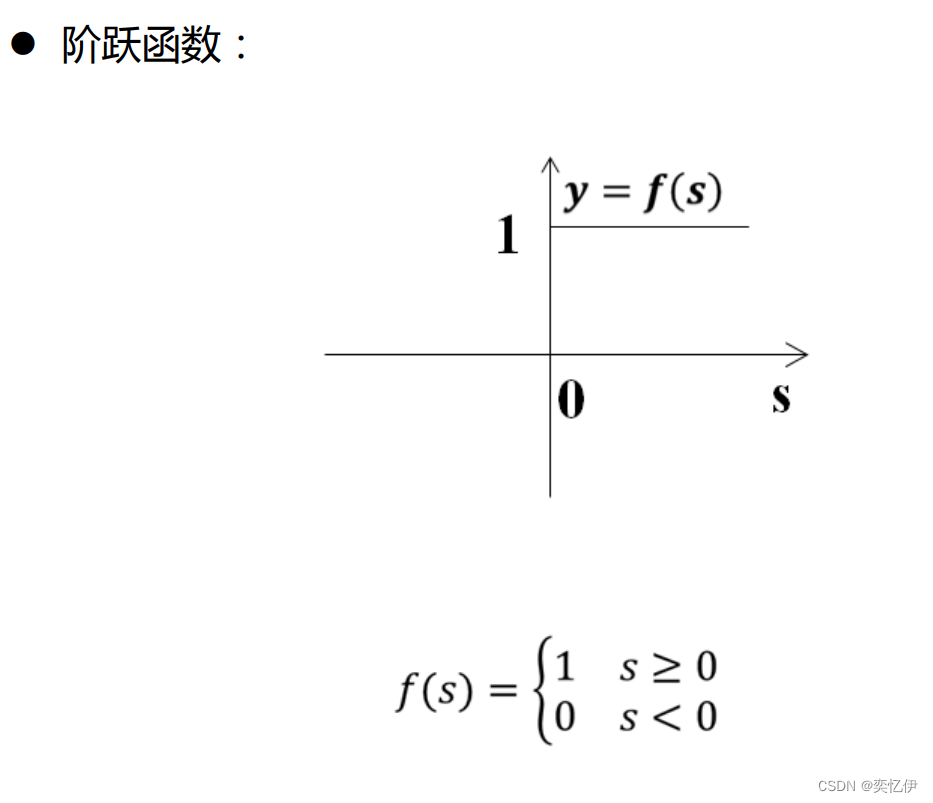
3.激活函数
在激活函数中加入非线性因素可以使划分更理想。
列出几种常见的非线性激活函数
4.小结
单层感知机:模型中的激活函数多采用符号函数,因此输出值为二值量,主要用于简单模式分类。
多层感知机:模型通过感知器的组合以及采用S型激活函数,可输出值为0-1之间的连续值,可实现输入到输出的任意非线性映射。
二·BP神经网络
BP神经网络=多层感知机+误差反向传播学习(训练)算法
即模型训练或者说连接权重的调整采用反向传播学习算法
误差反向传播学习算法
1.基本概念
学习的过程: 神经网络在外界输入样本的刺激下不断改变网络的连接权值,以使网络的输出不断地接近期望的输出。 信号正向传播→误差反向传播
学习的本质: 对各连接权值的动态调整 。
学习规则(算法): 权值调整规则,即在学习过程中网络中各神经元的连接权变化所依据的一定的调整规则。
类型: 监督学习——已知样本数据及其期望值( 标签值)
核心思想: 将输出误差以某种形式通过隐藏层向输入层逐层反传,将误差分摊给各层的所有神经元,修正各神经元权值 。
步骤:
1. 正向传播: 输入样本---输入层---各隐层---输出层
2. 判断是否转入反向传播阶段: 若输出层的实际输出与期望的输出不符
3. 误差反传:误差以某种形式在各层表示----修正各层单元的权值
4. 终止条件:网络输出的误差减少到可接受的程度进行到预先设定的学习次数为止
2.建立过程
(1)建立网络结构
其中的变量定义如下:
(2)初始化网络
①给各个连接权值分别指定一个(-1,1)内的值,设置误差函数e,给定计算精度ξ(误差可接受程度)和最大学习次数M。
②选定一组已知的输入和输出数据
(3)开始计算
依次计算各层的输入和输出
然后将预期输出和计算输出带入误差函数,计算误差
3.学习过程
BP网络学习的目的是为了使误差达到最小值。
也就是误差函数最优化的问题。这里就要用到梯度下降法。
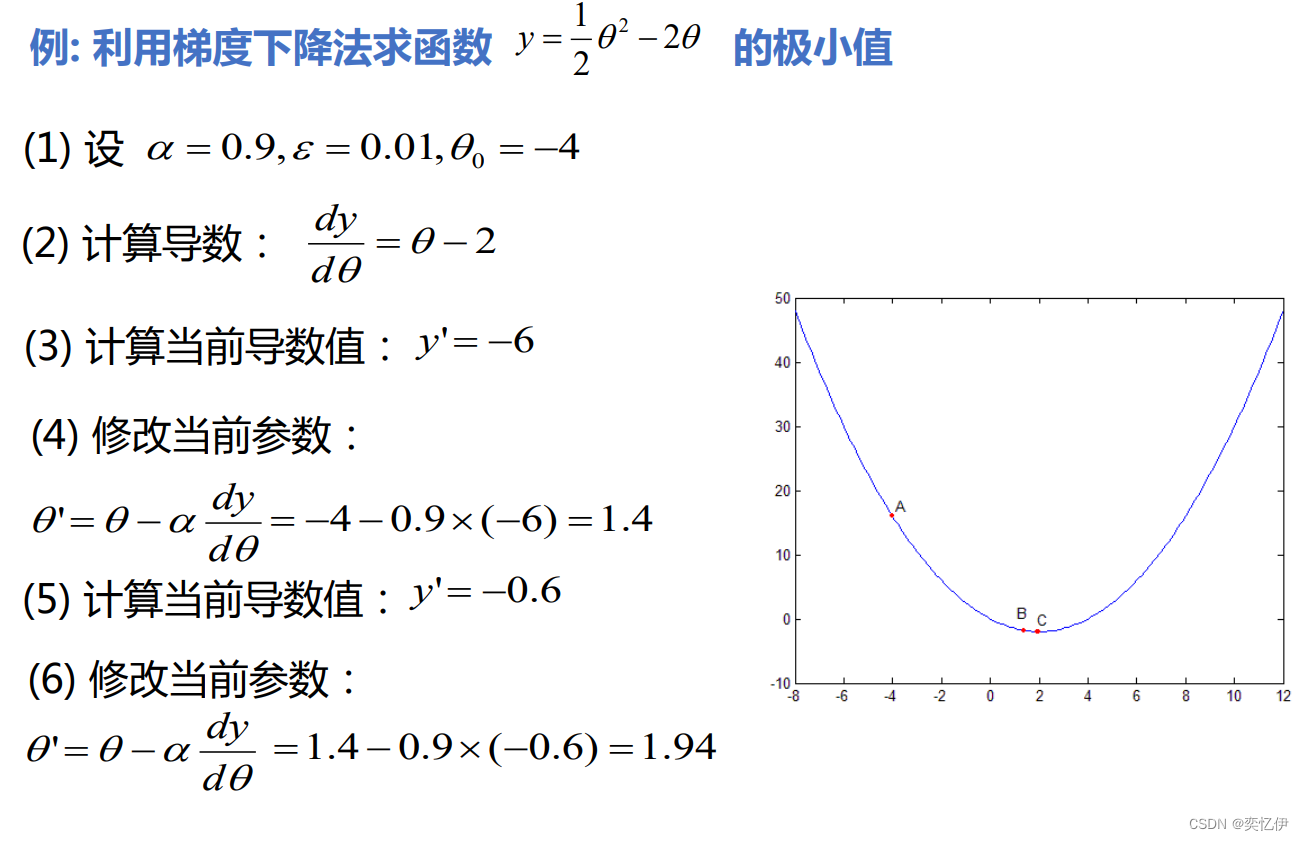
梯度下降法
假设我们爬山,如果想最快上到山顶,那么我们应该从山势最陡的地方上山。也就是山势变化最快的地方上山。如果我们想最快下山,那么沿着最快上山的路径,按反方向走,也是可行的。
同样,如果从任意一点出发,需要最快搜索到函数最大值,那么我们也 应该从函数变化最快的方向搜索。函数变化最快的方向是函数的梯度方向。所以求函数的最小值,可以按照梯度的反方向寻找(负梯度方向)。
根据数学理论,函数梯度就是对参数求偏导。建立网络时的阈值和连接权重都可看做误差函数的参数。
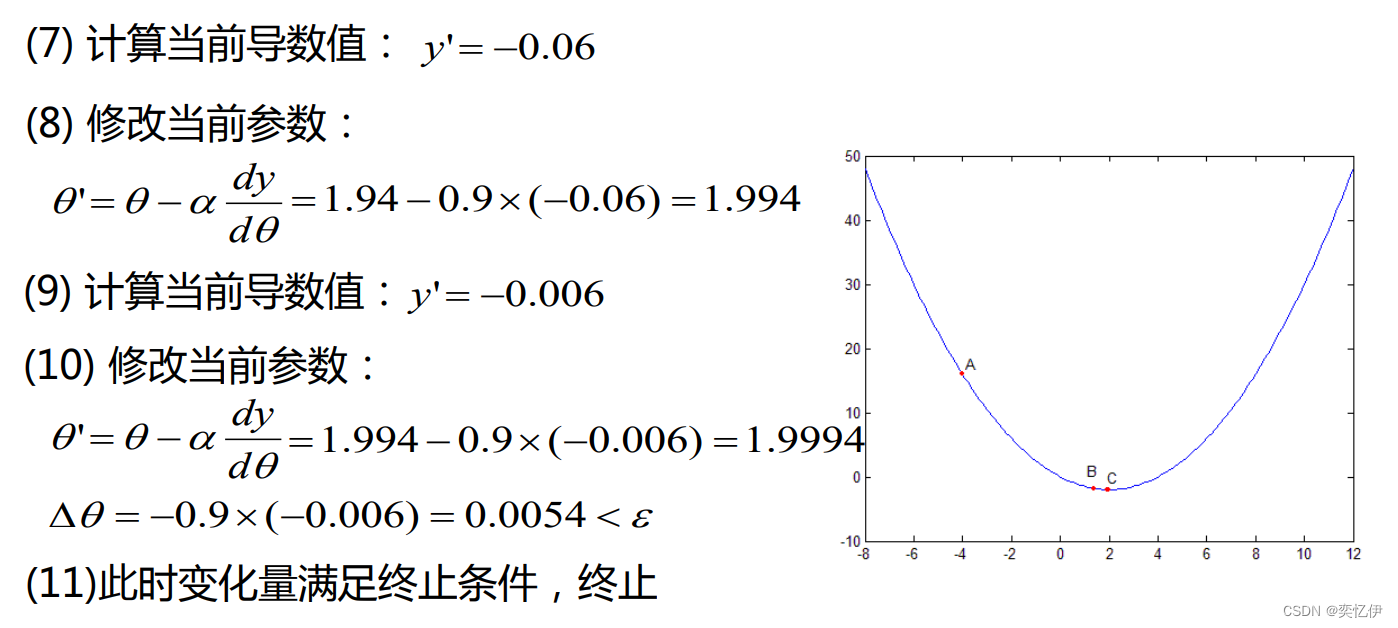
简单步骤如下
α也可以理解为每次确定下山方向前走的步长。
*关于学习率
α过大容易“越过”极值点,导致不收敛,过小则收敛速度慢 随着迭代次数的增加,一般要慢慢减小α (直观上,一开始前进快点,然后放慢速度)
下面看一个简单的实例
4.回到误差反向传播学习算法
同理各个神经元的连接权可以按如下修正:
修正值=初值-学习率*梯度
计算误差函数对输出层与隐含层的各神经元连接权值的偏导数 ,δ(k)为误差函数对输出的偏导
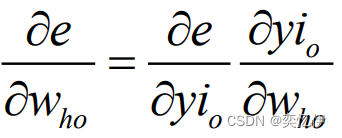
带入修正式可得:
同理得到输入层与隐含层连接权值的修正:
最后计算全局误差,满足精度学习结束
三·基于MATLAB的BP神经网络工具箱
(一)导入训练数据
1.将.mat后缀的文件导入MATLAB
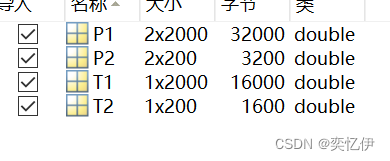
打开我们的.mat文件可以看到里面有四个数组,分别是P1,P2,T1,T2
使用load命令导入
load data.mat P1 T1 P2 T2可以给训练数据排序,画出训练数据的样图
[m,n]=sort(T1);
figure(1)
plot3(P1(1,n),P1(2,n),m)
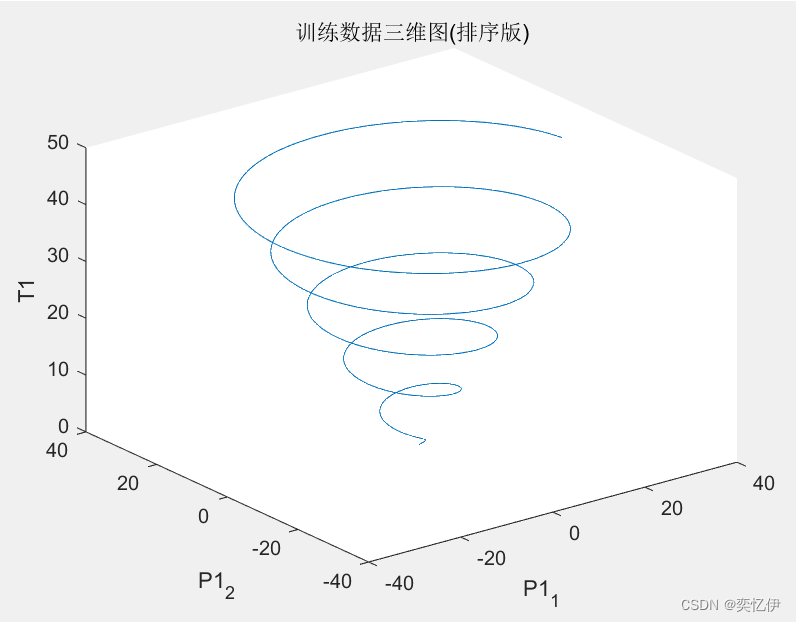
title('训练数据三维图(排序版)')
zlabel('T1')
xlabel('P1_1')
ylabel('P1_2')排序函数sort
可以对数组中的元素进行升序排序
[B,index]=sort(A)
B代表排序后的数组,index是排序后的元素对应排序之前的索引,A是待排序的数组
例子:
一维数组:单行或者单列按升序排,排序后的数组B中,第一个元素‘1’在原数组的索引为5
多维数组:每一列按升序排,数组D的第一列元素还是‘4’和‘7’,顺序变了,‘4’从一列2行到了一列1行。
(二)数据归一化处理
为了避免不同数量级数据之间的影响,需要把数据进行归一化
1.归一化函数
归一化函数mapminmax
mapminmax(A)函数对将矩阵中的每一行数据进行标准化处理, 每一行数据标准化到ymin和ymax。
[y,ps]=mapminmax(x,ymin,ymax)
x是变换前的矩阵,y是归一化后的矩阵,ps为记录标准化映射 的结构体。
如果不设置ymin和ymax默认是归一化到[-1,1]。
例子:
2.反归一化
训练得到的输出结果需要反归一化,才能得到实际的输出结果
需要先使用
mapminmax('apply',K,PS);
才能使用如下的反归一化
mapminmax('reverse',L,PS);
例子
X=[4 5 6;7 8 9];
M = [2 3;4 5];
[Y,PP] = mapminmax(X,0,1);%先把X按照最小为0,最大为1归一化得到Y,PP是X到Y的映射
N = mapminmax('apply',M,PP) %让M按照X的归一化方式得到N,沿用X到Y的映射PP
B = mapminmax('reverse',N,PP) %反归一化N
结果:
参考:Matlab归一化函数(mapminmax),作者:青风骏马
(三)构建BP神经网络
1.创建神经网络函数
创建神经网络函数newff
net = newff(P,T,S)
其中,net是新创建的一个BP神经网络,P是训练样本的输入数据矩阵(每一列一个样本),
T是训练样本的输出数据矩阵(每一列一个样本),S是一个设置各隐含层节点数量的向量。
2.设置参数
神经网络常用参数配置:
net.trainParam.epochs :最大学习次数 (默认100)
net.trainParam.lr :学习率 (默认0.01)
net.trainParam.goal :最小允许误差
例子:
net.trainParam.epochs=100;
net.trainParam.lr=0.01;
net.trainParam.goal=0.0004;3.训练BP神经网络
训练BP神经网络函数train
net=train(net,P,T)
net是新建好的网络,P是训练样本的输入数据矩阵(每一列 一个样本),T是训练样本的输出数据矩阵(每一列一个样本)
4.用已训练的BP神经网络做预测输出
预测输出函数sim
Y=sim(net,Q)
net是已训练的网络,Y是模型输出数据,Q是待测试的数据
注意:待测试的数据Q要按照训练数据进行归一化,最后输出数据Y要反归一化才是实际预测数据
四·实例
任务要求:
(1)从 data.mat 文件中分别读取训练数据集和测试数据集,其中 P1 是训练集输入数据,T1 是训练集输出数据,P2 测试集输入数据、T2 是测试集输出数据,并绘制出训练数据的三维函数图。
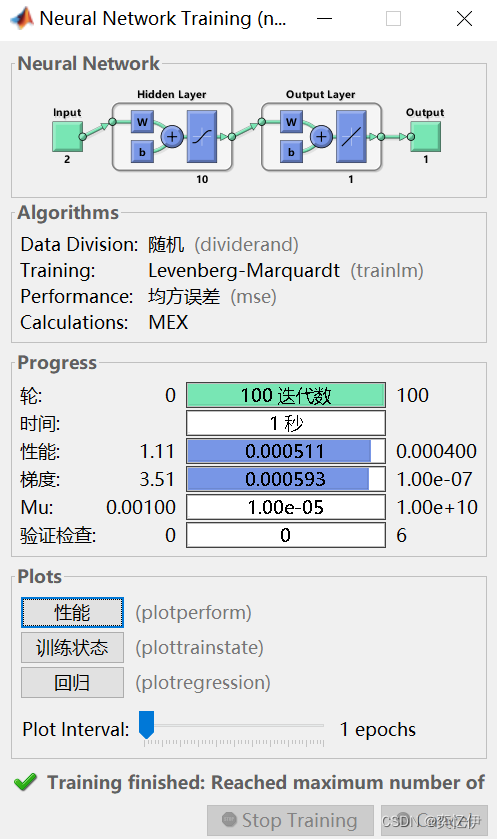
(2)训练 3 层 BP 神经网络,输入层有 2 个节点,隐含层有 10 个节 点,输出层有 1 个节点,迭代次数为 100,学习率为 0.1,最大训练 误差为 0.0004。
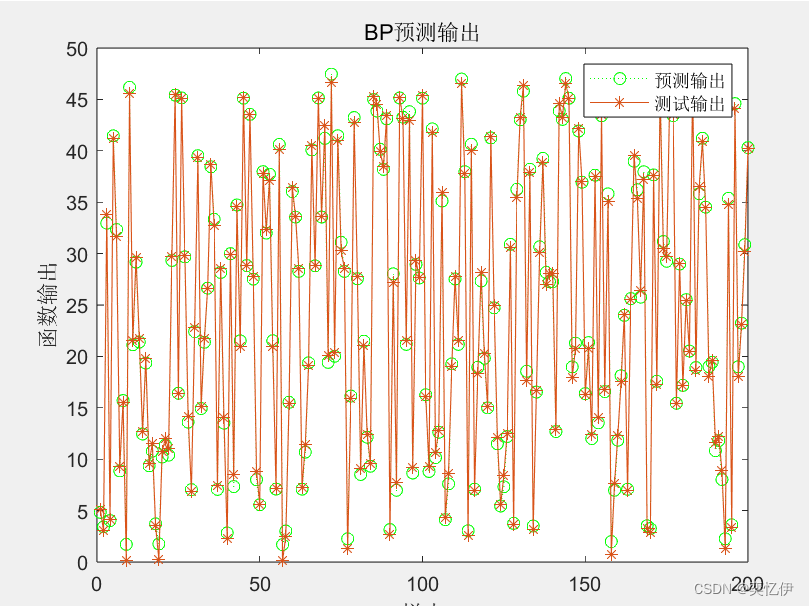
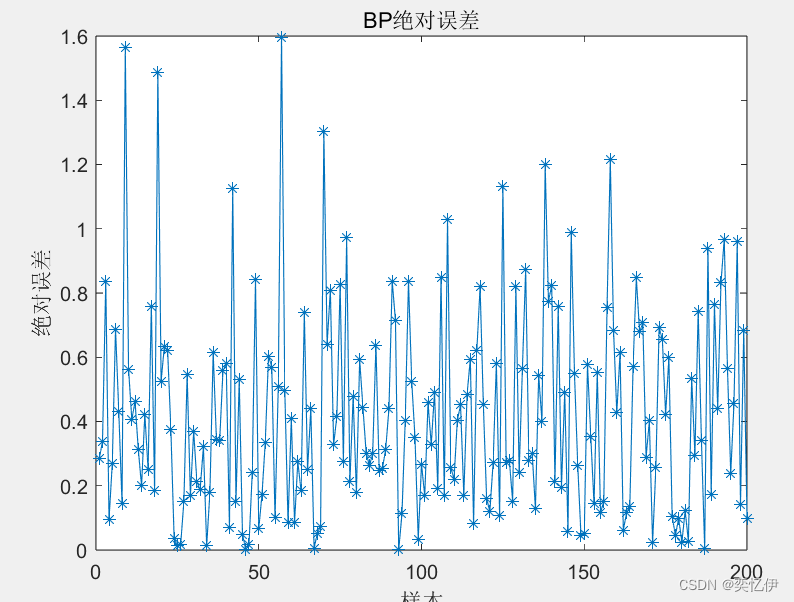
(3)用训练好的 BP 神经网络预测非线性函数输出,绘制预测输出和 期望输出的测试结果图和绝对误差图。
%把data.mat文件中P1,T1,P2,T2数据导入
load data.mat P1 T1 P2 T2
figure(1);
plot3(P1(1,:),P1(2,:),T1)
title('训练数据三维图(未排序版)')
zlabel('T1')
xlabel('P1_1')
ylabel('P1_2')
%下面是排列过的数据
%[排列好的数组变量,之前数组的索引]=sort(未排列的数组)
[m,n]=sort(T1);
figure(2)
plot3(P1(1,n),P1(2,n),m)
title('训练数据三维图(排序版)')
zlabel('T1')
xlabel('P1_1')
ylabel('P1_2')
%训练数据归一化
[inputn,inputps]=mapminmax(P1);
[outputn,outputps]=mapminmax(T1);
%构建神经网络
%输入层的两个节点体现在输入数据有两行,输出层的一个节点体现在输出数据有一行
%隐含层有10个节点
net=newff(inputn,outputn,10);
%网络参数配置
net.trainParam.epochs=100;
net.trainParam.lr=0.1;
net.trainParam.goal=0.0004;
%训练
net=train(net,inputn,outputn);
%预测
%预测数据归一化
inputn_test=mapminmax('apply',P2,inputps);
%预测输出
an=sim(net,inputn_test);
%输出结果反归一化
BPoutput=mapminmax('reverse',an,outputps);
%输出图形
figure(3)
plot(BPoutput,':og');
hold on;
plot(T2,'-*')
legend('预测输出','测试输出')
title('BP预测输出')
ylabel('函数输出')
xlabel('样本')
%绝对误差
error=abs(BPoutput-T2);
figure(4)
plot(error,'-*')
title('BP绝对误差')
ylabel('绝对误差')
xlabel('样本')
结果:
附:如需完整实验可私信