此博客停止更新迁移至SnailDove’s Blog，查看本文点击此处

目录

笔记源自：清华大学公开课：线性代数2——第8讲：图和网络

这门公开课参考教材：Gilbert Strang, Introduction to linear algebra, Wellesley-Cambridge Press,2016 ，本讲源自此书的第十章

提示：如果文中图片看不清文字，请右键单击鼠标，选择在新窗口打开图片，然后放大图片（这边上传之前都是可以看清的，由于网页正文部分大小固定，因此图片被自动缩小以便适配网页），截图部分是课堂ppt老师随手的板书。

简介

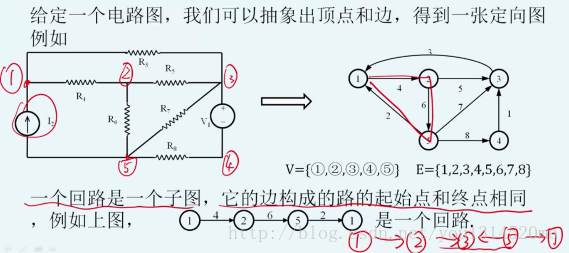
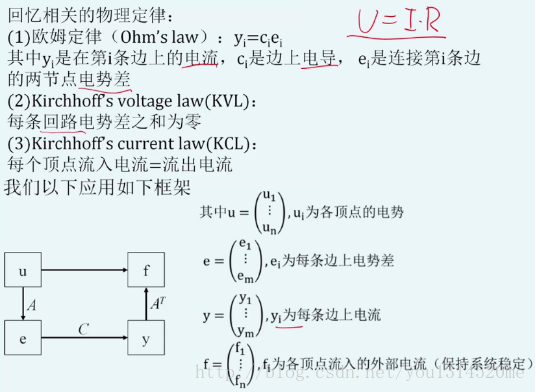
欧姆定律Ohm’s law的向量形式

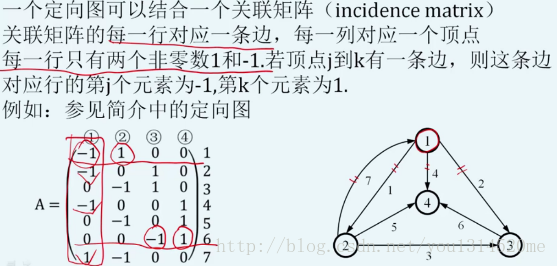
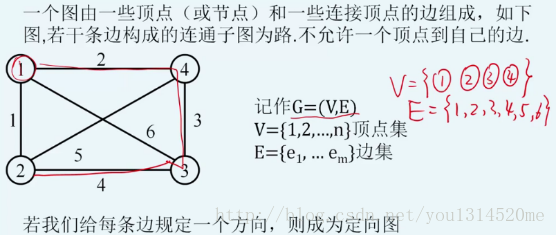
图与矩阵

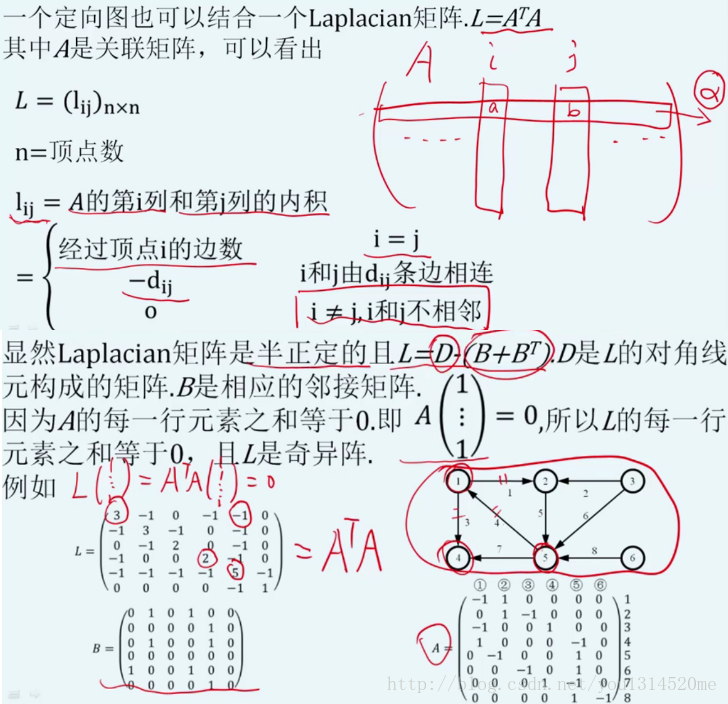
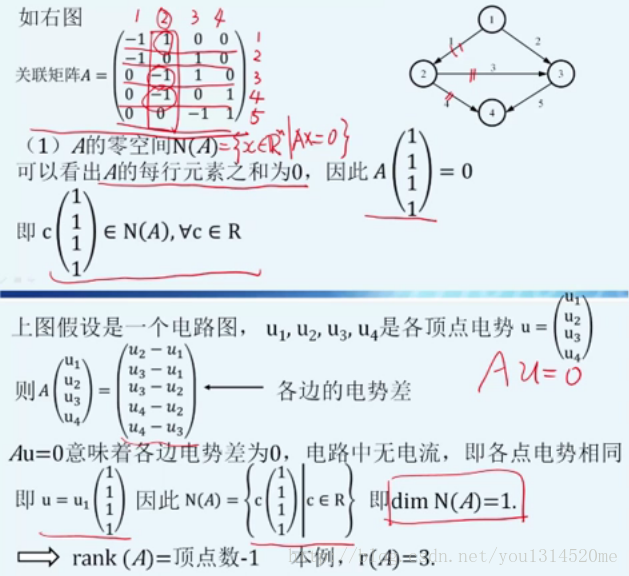
关联矩阵incidence matrix

邻接矩阵adjacency matrix

拉普拉斯矩阵laplacian matrix

注： 半正定证明与刚度矩阵类似

网络和加权Laplacian矩阵

电路相关的物理定律

例子

不接外部源

接外部源

带权$K=A^TCA$

关联矩阵的四个基本子空间

N(A)

C(A)

按$C(A)$的定义得：$C(A)=\{Ax|x\in R^n\}$ 。沿用前面使用的字母：$u$是各点电势，$e$是各边电势差，$Au=e$ ，当$Au=e$ 有解 $\Leftrightarrow e \in C(A)$

1. 去证明：$dim(C(A))=n-1$ ，即$A$ 的任意 $n-1$个列向量是线性无关的。设$A=(a_1,a_2,\,...\,,a_n)$，不妨假设$a_1,a_2,\,...\,,a_{n-1}$线性相关，那么存在$c_1, c_2,\,...\,,c_{n-1} \in R$ 且不全为0满足：$c_1a_1+c_2a_2+...+c_{n-1}a_{n-1}+0a_n=0\Rightarrow A\begin{pmatrix}c_1\\c_2\\.\\.\\.\\c_{n-1}\\0\end{pmatrix}={0}\Rightarrow \begin{pmatrix}c_1\\c_2\\.\\.\\.\\c_{n-1}\\0\end{pmatrix}\in N(A),$但与$N(A)=\left\{c\begin{pmatrix}1\\.\\.\\.\\1\end{pmatrix} \Bigg| c\in R \right\}$ 矛盾，以此类推，得以证明$C(A)$的维数是$n-1$ ，即$A$的任意$n-1$个列向量均可作为$C(A)$的一组基。

2. 发现矩阵中对应的回路：$e\in C(A)$ 如下等式有解 $Au=e\Rightarrow \begin{pmatrix}-1&1&0&0\\-1&0&1&0\\0&-1&1&0\\0&-1&0&1\\0&0&-1&1\end{pmatrix}\begin{pmatrix}u_1\\u_2\\u_3\\u_4\\u_5 \end{pmatrix}=\begin{pmatrix}e_1\\e_2\\e_3\\e_4\\e_5 \end{pmatrix} \Rightarrow \begin{cases}-u_1+u_2=e_1\\-u_1+u_3=e_2\\-u_2+u_3=e_3\\-u_2+u_4=e_4\\-u_3+u_4=e_5\end{cases} \Rightarrow \begin{cases}e_1-e_2+e_3=0\\e_3-e_4+e_5=0\end{cases}$ ，即边1,2,3这3条边电势差之和为0，由图上可得边1,2,3恰好构成一个回路，边3,4,5也一样。这恰好是Kirchholff Voltage Law (KVL)。把这两个回路等式书写成矩阵形式$\begin{pmatrix}1&-1&1&0&0\\0&0&1&-1&1 \end{pmatrix}\begin{pmatrix} e_1\\e_2\\e_3\\e_4\\e_5 \end{pmatrix}=0$ . 此时称矩阵$B =\begin{pmatrix}1&-1&1&0&0\\0&0&1&-1&1 \end{pmatrix}$ 为回路矩阵，可以看到它的每一行代表一个回路且称为极小回路，每一列代表一条边。如果边的方向是逆时针方向则取为正号，否则取为负号。注意，此时$e\in N(B)$。

3. 此外，$BA=\begin{pmatrix}1&-1&1&0&0\\0&0&1&-1&1\end{pmatrix}\begin{pmatrix}-1&1&0&0\\-1&0&1&0\\0&-1&1&0\\0&-1&0&1\\0&0&-1&1\end{pmatrix}=\begin{pmatrix}0&0&0&0\\0&0&0&0\end{pmatrix}$即$C(A) \subseteq N(B)$ 。$dim(N(B))=3, dim(C(A))=3$，因此$C(A)$就构成了$N(B)$的基。从理意义角度理解：$A$矩阵执行的操作表示求解各边电势之差，$B$各行刚好是回路，由$KVL$定律得结果必为0.

$N(A^T)$

1. 由定义得：$N(A^T)=\{y\in R^m|A^Ty=0\}$。例子中，关联矩阵$A$ 各行代表一条边，各列代表一个顶点。那么$A^T$ 的行代表顶点，列代表边。
   $A^Ty=0\Rightarrow\begin{pmatrix}-1&-1&0&0&0\\1&0&-1&-1&0\\0&1&1&0&-1\\0&0&0&1&1\end{pmatrix}\begin{pmatrix}y_1\\y_2\\y_3\\y_4\\y_5 \end{pmatrix}=\begin{pmatrix}0\\0\\0\\0\\0\end{pmatrix} \Rightarrow \begin{cases}-y_1-y_2=0\\y_1-y_3-y_4=0\\y_2+y_3-y_5=0\\y_4+y_5=0\end{cases}$
   物理意义解读：$y_i$是各第$i$边上的电流，上述等式表明每一个顶点输入输出电流和为0，即Kichhoff Current Law (KCL)。

2. $A^Ty=0$， 由前文得到：
   $BA=0 \Rightarrow A^TB^T=0 \Rightarrow A^TB^T=\begin{pmatrix}-1&-1&0&0&0\\1&0&-1&-1&0\\0&1&1&0&-1\\0&0&0&1&1\end{pmatrix}\begin{pmatrix}1&0\\-1&0\\1&1\\0&-1\\0&1\end{pmatrix}=\begin{pmatrix}0&0\\0&0\\0&0\\0&0\end{pmatrix}$
   因此，$C(B^T) \subseteq N(A^T)$。由于$r(A)=C(A)=r=n-1, N(A^T)+C(A)=m, N(A^T)=m-r=5-3=2$， 由于$B^T$的列向量线性无关，即$B$的行向量代表回路，那么回路向量就是$N(A^T)$的一组基。

$C(A^T)$

总结

• $N(A_{m\times n})$零空间 $Au=0$ ，$N(A)=c{(1,1,\,...\,,1)^T}_{n\times 1}$ ；物理意义：各点电势相等，电势差为0。
• $C(A_{m\times n})$列空间 $Au=e$(上文用的是x, b)，$A$ 中任意$n-1$ 列构成了$C(A)$ 的一组基；物理意义每个极小回路电势守恒，每个极小回路构成的极大回路电势依然守恒，诠释了KVL定律。
• $N(A^T)$左零空间 $A^Ty=0$，回路向量构成了$N(A^T)$ 的一组基；诠释了无外部电流源的KCL定律。
• $C(A^T)$行空间 ，$A^Ty=f$， 每个极大树子图对应关联矩阵的行向量（即边）构成了$C(A^T)$ 的一组基；诠释了有外部电流源的KCL定律。

注计

N(B)=C(A)

B的零空间中的任何一个向量，它都要属于A的列空间，$A$的列空间中的每一个向量的特点，比如说$A$乘上一个$x_1$到$x_n$，$x_1$到$x_n$是$n$个顶点的电势。$A$乘上这个向量得到的是各个边上的电势差，那么相应的$x_j-x_k$就是$j$和$k$两个顶点上的电势差，顶点连线，$j$和$k$连线的边上的电势差。那么我们要想说明，N（B）中的向量属于C（A）那么我们只要说明任何一个向量属于B的零空间，它最后都能写成这样一种形式，就可以了。那么设$e$属于$N(B)$，那么我们可以取定这个连通图的一个极大树子图，然后在这个极大树子图$T$上取一个顶点作为基点，那么任意的另外一个顶点$K$跟这个基点之间它们连线的路在$T$上只有一条这样的路，因为$T$是一个树，它不可能有回路，所以在$T$中有唯一的一条连接K到基点的路。定义K的电势：在这条路上各边的电势之和，各边的电势之和，我们这个$e_1$到$e_m$呢，我们可以刻画各个边上的电势，那么我们可以看到$e$属于$N(B)$我们实际上可以检查出任意边上的电势差实际上是$e_j$等$u_k$减$u_1$，那么其中的这个$k$呢为j的起点，$l$为$j$的终点，最后我们就可以得到$e=-Au$，所以$e$就属于$C(A)$就是这个地方呢，我们要使用$e$属于$N(B)$，我们才能检查出：任意边上的这个电势差等于$u_k$减$u_l$，就是要满足科尔霍夫电压定律。

欧拉公式Euler’s formula

对于$B_{x \times m}\Rightarrow C(B^T)+dim(N(B))=r_B+dim(N(B))=m\Rightarrow m-r_B=dim(N(B))=dim(C(A))=n-1$

又因为欧拉公式：$m-l=n-1$，得：$r_B=l$，即 B B <script type="math/tex" id="MathJax-Element-104">B</script>是行满秩的，其实极小回路组对应极大线性无关组。