超级详细的红黑树底层代码实现 [万字详解，速来一看]

红黑树详解与实现

红黑树简介

红黑树（Red-Black Tree）是一种 自平衡二叉搜索树。它具有二叉搜索树的特性，且通过颜色标记节点和特定规则，确保树的高度接近最小，从而保证插入、删除和查找操作的时间复杂度为 (O(\log n))。相比于其他平衡二叉树如 AVL 树，红黑树在插入和删除操作上更高效，因为它允许树稍微偏离完美平衡，从而减少旋转次数。

红黑树常被用于 操作系统、数据库管理系统 中的调度和存储结构，例如 Linux 内核的进程调度、C++ STL 的 map 和 set 容器等。

红黑树的性质

红黑树有以下几个关键性质，它们确保了树的自平衡：

每个节点是红色或黑色：
- 每个节点都要么是红色，要么是黑色。
根节点是黑色：
- 树的根节点必须是黑色。
红色节点的子节点是黑色：
- 如果一个节点是红色，它的两个子节点必须是黑色，避免两个连续的红色节点。
每个节点到其每个叶子节点的所有路径包含相同数量的黑色节点：
- 这条性质保证了树的高度接近最小，确保操作的效率。
叶子节点（NIL节点）是黑色：
- 红黑树中的叶子节点通常表示为 null 或 NIL，这些节点按定义是黑色的。

这些性质确保了红黑树的路径长度保持在一个合理范围内，避免了退化成链表的情况，因此插入、删除、查找操作的最坏时间复杂度为 (O(\log n))。

红黑树的操作

插入操作

红黑树的插入遵循二叉搜索树的插入规则，同时为了保持红黑树的性质，插入后可能会触发修正操作。插入新节点时，默认将新节点着色为红色。这样可以确保不会违反 黑色平衡 的性质，但可能会导致两个连续的红色节点，这需要通过旋转和重新着色进行修正。

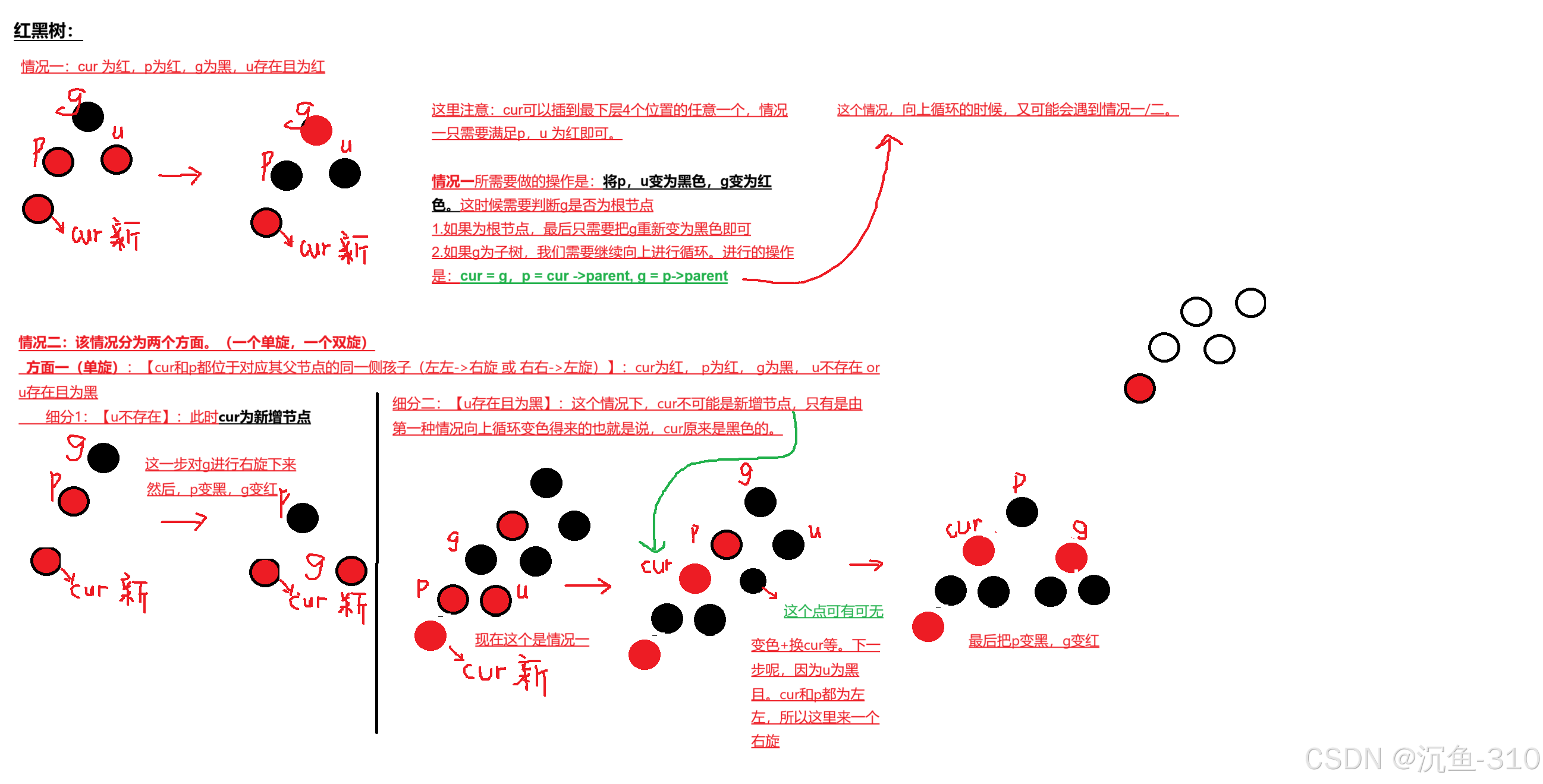
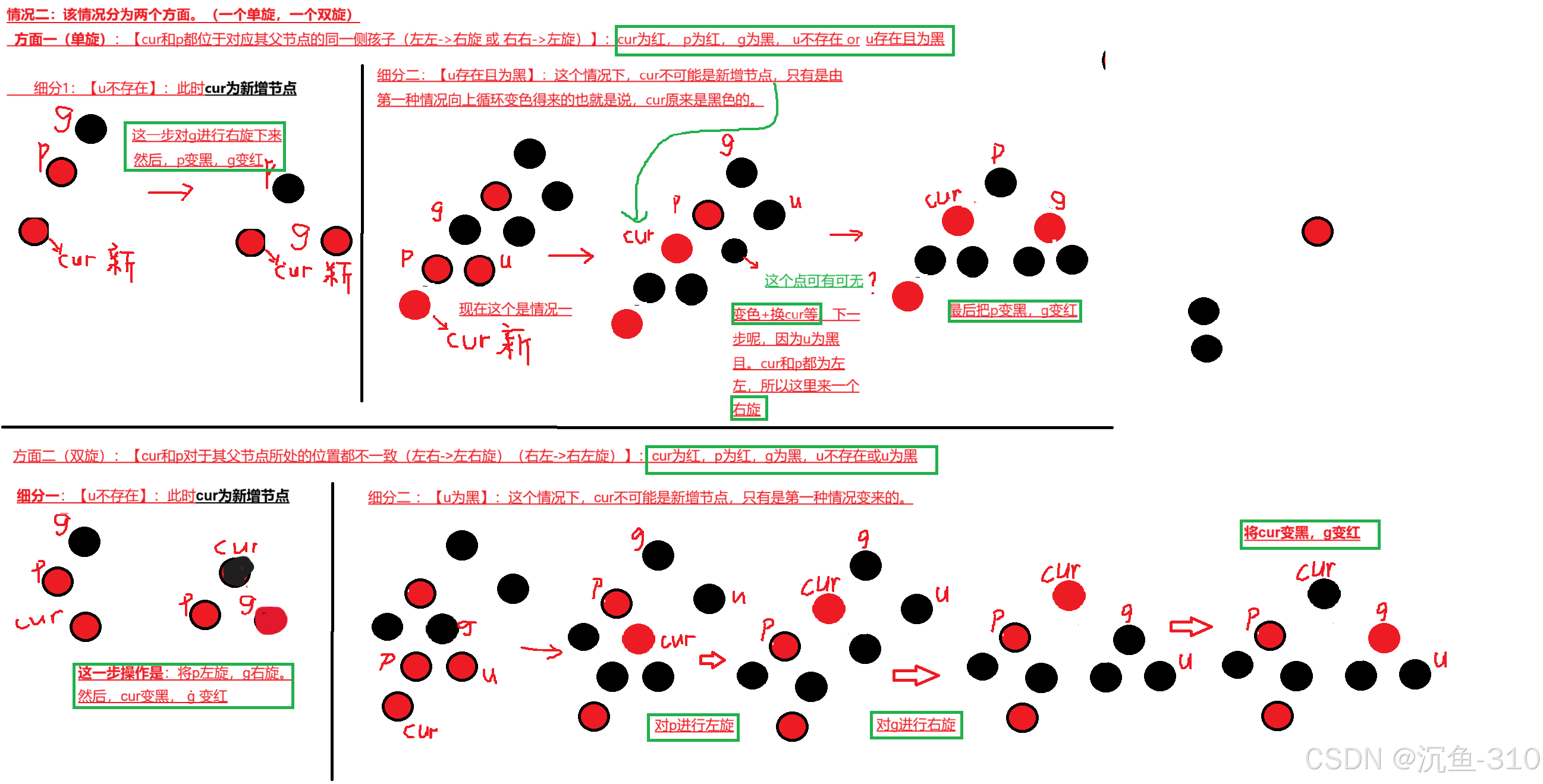
修正操作分为以下几种情况：

情况1：叔叔节点为红色。此时我们将父节点和叔叔节点都变成黑色，将祖父节点变成红色，并继续向上调整。
情况2：叔叔节点为黑色且当前节点是左子节点或右子节点。根据当前节点相对父节点的位置，进行相应的旋转（左旋或右旋），并交换颜色来保持平衡。

删除操作

红黑树的删除较为复杂，因为删除黑色节点可能会导致路径上黑色节点数量不平衡。为了解决这个问题，删除后也需要进行修正操作，包括重新着色和旋转。和插入一样，删除操作的时间复杂度同样是 (O(\log n))。

旋转操作

旋转是红黑树中保持平衡的核心操作。它分为左旋和右旋：

左旋：将当前节点的右子节点提升为父节点，当前节点变为右子节点的左子节点。
右旋：将当前节点的左子节点提升为父节点，当前节点变为左子节点的右子节点。

通过旋转操作，可以调整树的形态，并确保它满足红黑树的性质。

红黑树的实现

接下来，我们通过 C++ 的代码来实现一个红黑树，涵盖插入、旋转、中序遍历等操作。

引入库文件和基本设置

首先引入必要的头文件并定义颜色枚举类型：

#pragma once
#include<iostream>
#include <set>
#include <map>
#include <string>

using namespace std;

// 枚举定义红黑树节点的颜色，红色或黑色
enum Colour
{
    RED,
    BLACK,
};

红黑树节点的定义

接着定义红黑树节点的结构体模板：

template<class K, class V>
struct RBTreeNode
{
   pair<K, V> _kv;                    // 键值对，存储键和值
   RBTreeNode<K, V>* _left;           // 指向左子树
   RBTreeNode<K, V>* _right;          // 指向右子树
   RBTreeNode<K, V>* _parent;         // 指向父节点
   Colour _col;                       // 记录节点颜色

   // 构造函数，初始化节点
   RBTreeNode(const pair<K, V>& kv)
   :_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED) // 初始颜色为红色
   {}
};

红黑树类的定义与析构函数

定义红黑树类模板，并实现析构函数用于递归销毁节点：

template<class K, class V>
class RBTree
{
    typedef RBTreeNode<K, V> Node;     // 定义别名，便于引用
 private:
    Node* _root = nullptr;             // 树根节点指针

 public:
     // 析构函数，调用Destroy函数删除所有节点，释放内存
     ~RBTree()
     {
         Destroy(_root);
     }

     // 递归销毁节点，删除树
     void Destroy(Node *root)
     {
         if (root == nullptr)
             return;
         Destroy(root->_left);
         Destroy(root->_right);
         delete root;
     }

插入节点的逻辑

下面的代码实现了红黑树的插入操作，按照二叉搜索树的规则插入新节点。如果树为空，则将新节点作为根节点并设为黑色：

    // 插入函数，插入键值对
    bool Insert(const pair<K, V>& kv)
    {
        if (_root == nullptr) // 树为空时插入根节点
        {
            _root = new Node(kv);
            _root->_col = BLACK;  // 根节点颜色设为黑色
            return true;
        }

        Node* parent = nullptr;   // 用于指向父节点
        Node* cur = _root;        // 当前节点从根开始

        // 寻找插入位置，基于二叉搜索树规则
        while (cur)
        {
            if (cur->_kv.first < kv.first)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_kv.first > kv.first)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                return false;     // 如果键已经存在，返回false
            }
        }

        // 创建新节点并设为红色
        cur = new Node(kv);
        cur->_col = RED;

        // 将新节点插入到父节点的左或右
        if (parent->_kv.first < kv.first)
        {
            parent->_right = cur;
            cur->_parent = parent;
        }
        else
        {
           parent->_left = cur;
           cur->_parent = parent;
        }

红黑树的调整：插入修正

以下是红黑树变色调整的详细图解

在这里插入图片描述

插入新节点后，可能会破坏红黑树的平衡。为了恢复平衡，我们需要根据红黑树的性质进行修正：

        // 插入后调整红黑树，确保平衡性
        while (parent && parent->_col == RED)
       

 {
            Node* grandParent = parent->_parent;

            // Parent为grandParent的左子节点
            if (parent == grandParent->_left)
            {
                Node* uncle = grandParent->_right;

                // 情况1：叔叔节点为红色，改变颜色并向上调整
                if (uncle && uncle->_col == RED)
                {
                    parent->_col = uncle->_col = BLACK;
                    grandParent->_col = RED;
                    cur = grandParent;
                    parent = cur->_parent;
                }
                else
                {
                    // 情况2：叔叔节点为黑色且当前节点为左子节点，右旋转grandParent
                    if (parent->_left == cur)
                    {
                        RotateR(grandParent);
                        swap(parent->_col, grandParent->_col);
                    }
                    else
                    {
                        // 情况3：当前节点为右子节点，左旋转parent，再右旋转grandParent
                        RotateL(parent);
                        RotateR(grandParent);
                        cur->_col = BLACK;
                        grandParent->_col = RED;
                    }
                    break;
                }
            }
            else // Parent为grandParent的右子节点
            {
                Node *uncle = grandParent->_left;

                // 情况1：叔叔节点为红色
                if (uncle && uncle->_col == RED)
                {
                    parent->_col = uncle->_col = BLACK;
                    grandParent->_col = RED;
                    cur = grandParent;
                    parent = cur->_parent;
                }
                else
                {
                    // 情况2：叔叔为黑色且当前节点为右子节点，左旋grandParent
                    if (parent->_right == cur)
                    {
                        RotateL(grandParent);
                        swap(parent->_col, grandParent->_col);
                    }
                    else
                    {
                        // 情况3：当前节点为左子节点，右旋转parent，左旋转grandParent
                        RotateR(parent);
                        RotateL(grandParent);
                        cur->_col = BLACK;
                        grandParent->_col = RED;
                    }
                }
            }
        }
        _root->_col = BLACK;  // 根节点必须为黑色
        return true;
    }

中序遍历

中序遍历用于按照升序遍历红黑树中的键值对。下面是实现代码：

    // 中序遍历红黑树的外部接口
    void Inorder()
    {
        _Inorder(_root);
    }

    // 中序遍历红黑树，递归遍历左子树->根->右子树
    void _Inorder(Node *root)
    {
        if (root == nullptr)
        {
            return;
        }
        _Inorder(root->_left);                     // 递归遍历左子树
        cout << root->_kv.first << " " << root->_kv.second << endl;  // 打印键值对
        _Inorder(root->_right);                    // 递归遍历右子树
    }

左旋和右旋操作

旋转操作是红黑树保持平衡的核心操作。以下是左旋和右旋的实现：

    // 左旋转函数
    void RotateL(Node *parent)
    {
        Node *subR = parent->_right;               // 右子节点
        Node *subRL = subR->_left;                 // 右子节点的左子节点

        parent->_right = subRL;                    // 左移subR的左子节点
        if (subRL)
            subRL->_parent = parent;

        Node *ppNode = parent->_parent;            // 父节点的父节点
        subR->_left = parent;                      // 旋转操作
        parent->_parent = subR;

        if (ppNode == nullptr)                     // 如果parent为根节点
        {
            _root = subR;
            _root->_parent = nullptr;
        }
        else
        {
            if (ppNode->_left == parent)           // 更新父节点的子树指向
            {
                ppNode->_left = subR;
            }
            else
            {
                ppNode->_right = subR;
            }

            subR->_parent = ppNode;
        }
    }

    // 右旋转函数
    void RotateR(Node *parent)
    {
        Node *subL = parent->_left;                // 左子节点
        Node *subLR = subL->_right;                // 左子节点的右子节点

        parent->_left = subLR;                     // 右移subL的右子节点
        if (subLR)
        {
            subLR->_parent = parent;
        }

        Node *ppNode = parent->_parent;            // 父节点的父节点
        subL->_right = parent;                     // 旋转操作
        parent->_parent = subL;

        if (ppNode == nullptr)                     // 如果parent为根节点
        {
            _root = subL;
            _root->_parent = nullptr;
        }
        else
        {
            if (ppNode->_left == parent)           // 更新父节点的子树指向
            {
                ppNode->_left = subL;
            }
            else
            {
                ppNode->_right = subL;
            }

            subL->_parent = ppNode;
        }
    }

红黑树平衡性检查

最后是红黑树的平衡性检查，验证红黑树是否满足所有性质：

    // 验证红黑树是否平衡，递归检查所有路径上的黑色节点数量
    bool Check(Node *root, int blackNum, const int ref)
    {
        if (root == nullptr) // 到达叶子节点，检查黑色节点数量是否一致
        {
            if (blackNum != ref)
            {
                cout<<"违反规则：每条路径经过的黑色节点数量不相等"<<endl;
                return false;
            }
            return true;
        }

        // 检查红色节点的父节点是否为红色
        if (root->_col == RED && root->_parent->_col == RED)
        {
            cout<<"违反规则：红色节点不能有红色节点作为父节点"<<endl;
            return false;
        }

        if (root->_col == BLACK)
        {
            ++blackNum; // 记录黑色节点数量
        }

        return Check(root->_left, blackNum, ref) && Check(root->_right, blackNum, ref);
    }

    // 判断红黑树是否平衡
    bool IsBalance()
    {
        if (_root == nullptr)
        {
            return true;
        }

        if (_root->_col != BLACK)
        {
            return false;
        }

        int ref = 0;
        Node *left = _root;
        while (left) // 循环找到最左侧黑色节点的数量
        {
            if (left->_col == BLACK)
            {
                ++ref;
            }
            left = left->_left;
        }

        return Check(_root, 0, ref); // 检查整棵树的黑色节点数量
    }
};

全部代码

这里要提一句，上面的代码块部分基于完整代码由GPT4O生成如果有与下面完整代码有冲突，请以下面内容为准

RBTree.hpp

#pragma once
#include<iostream>
#include <set>
#include <map>
#include <string>

using namespace std;
// 现在是连接的
//枚举类型
enum Colour
{
    RED,
    BLACK,
};

//定义红黑树节点结构体
template<class K, class V>
struct RBTreeNode
{
   pair<K, V> _kv;//键值对
   RBTreeNode<K, V>* _left;
   RBTreeNode<K, V> *_right;
   RBTreeNode<K, V> *_parent;
   Colour _col;//记录节点颜色
   
   //构造函数，初始化成员变量
   RBTreeNode(const pair<K, V>& kv)
   :_kv(kv)
   , _left(nullptr)
   , _right(nullptr)
   , _parent(nullptr)
   , _col(RED)//每次新加的节点都是红色的
   {}
   
}; 

template<class K, class V>
class RBTree
{
    typedef RBTreeNode<K, V> Node;
 private:
    Node* _root = nullptr;
 public:
     ~RBTree()//析构函数:调用Destroy函数（公共接口）
     {
         Destroy(_root);
     }

     void Destroy(Node *root)
     {
         if (root == nullptr)
             return;
         Destroy(root->_left);
         Destroy(root->_right);
         delete root;
     }

    bool Insert(const pair<K, V>& kv)
    {
        if(_root == nullptr)
        {
            _root = new Node(kv);
            _root->_col = BLACK;
            return true;
        }

        Node* parent = nullptr;
        Node* cur = _root;

        //基于搜索树规则找到插入位置
        while(cur)
        {
            
            if(cur->_kv.first < kv.first)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if(cur->_kv.first > kv.first)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                return false;

            }
        }

        cur = new Node(kv);
        cur->_col = RED;

        //插入节点
        if(parent->_kv.first < kv.first)
        {
            parent->_right = cur;
            cur->_parent = parent;
        }
        else
        {
           parent->_left = cur;
           cur->_parent = parent;
        }

        while(parent && parent->_col == RED)//只需要考虑这种情况，如果parent为空，或parent为黑则不需要调整
        {
            Node* grandParent = parent->_parent;

            if(parent == grandParent->_left)//首先我们先考虑parent是左孩子的情况：这种情况下会分成左左和左右两种情况
            {
                Node* uncle = grandParent->_right;
                //情况一：叔叔节点为红
                if(uncle && uncle->_col == RED)//如果叔叔节点存在且为红，则将parent和uncle节点都置为黑，将grandParent置为红，然后继续向上调整
                {
                    parent->_col = uncle->_col = BLACK;
                    grandParent->_col = RED;

                    cur = grandParent;
                    parent = cur->_parent;
                }
                else//这个是上面if的非，意思是叔叔节点不存在或者叔叔节点为黑
                {
                    //情况二：叔叔节点为黑，且cur为左孩子，形成左左，右旋g
                    if(parent->_left == cur)
                    {
                        RotateR(grandParent);
                        swap(parent->_col, grandParent->_col);
                    }
                    else//cur为右孩子，形成左右，先左旋parent，再右旋grandParent
                    {
                        //情况三
                        RotateL(parent);
                        //swap(parent->_col, grandParent->_col);
                        RotateR(grandParent);
                        cur->_col = BLACK;
                        grandParent->_col = RED;

                    }

                    break;
                }
            }
            else // 当parent为g的右孩子，此时与左孩子相反，但做法一致
            {
                Node *uncle = grandParent->_left;
                if (uncle && uncle->_col == RED)
                {
                    parent->_col = uncle->_col = BLACK;
                    grandParent->_col = RED;

                    cur = grandParent;
                    parent = cur->_parent;
                }
                else // 叔叔节点不存在或者叔叔节点为黑：旋转标志
                {
                    if (parent->_right == cur)
                    {
                        RotateL(grandParent);                  // 先左旋
                        swap(parent->_col, grandParent->_col); // 再交换颜色
                    }
                    else // cur为左孩子，形成右左，先右旋parent，再左旋grandParent
                    {
                        RotateR(parent);
                        RotateL(grandParent);
                        cur->_col = BLACK;
                        grandParent->_col = RED;
                    }
                }
            }

            
        
        }
        _root->_col = BLACK;
        return true;
    }

    //中序遍历红黑树
    void Inorder() // 这个是作对外的接口，因为实例化对象后不能调用下面那个函数，因为包含私有成员变量
    {
        _Inorder(_root);
    }

    void _Inorder(Node *root) // 做形参，递归中序遍历
    {
        if (root == nullptr)
        {
            return ;
        }

        _Inorder(root->_left);
        cout << root->_kv.first << " " << root->_kv.second << endl; // 这里打印的是key,打印出pair键值对.包含原根节点，以及左右子树的节点
        _Inorder(root->_right);
    }

    void RotateL(Node *parent)
    {
        Node *subR = parent->_right;
        Node *subRL = subR->_left;

        parent->_right = subRL;
        if (subRL)
            subRL->_parent = parent;

        Node *ppNode = parent->_parent;
        subR->_left = parent;
        parent->_parent = subR;

        if (ppNode == nullptr)
        {
            _root = subR;
            _root->_parent = nullptr;
        }
        else
        {
            if (ppNode->_left == parent)
            {
                ppNode->_left = subR;
            }
            else
            {
                ppNode->_right = subR;
            }

            subR->_parent = ppNode;
        }
    }

    void RotateR(Node *parent)
    {
        Node *subL = parent->_left;
        Node *subLR = subL->_right;

        parent->_left = subLR;
        if (subLR)
        {
            subLR->_parent = parent;
        }

        Node *ppNode = parent->_parent;
        subL->_right = parent;
        parent->_parent = subL;

        // if (_root == parent)
        if (ppNode == nullptr)
        {
            _root = subL;
            _root->_parent = nullptr;
        }
        else
        {
            if (ppNode->_left == parent)
            {
                ppNode->_left = subL;
            }
            else
            {
                ppNode->_right = subL;
            }

            subL->_parent = ppNode;
        }
    }

    bool Check(Node *root, int blackNum, const int ref)
    {
        //在这个函数中我们判断每条路径的黑色节点是否与ref相等，不i相等则返回false
        //同时我们需要当递归到红色节点的时候判断其父节点是否红色如果为红色则返回false

        if(root == nullptr)//第一次循环用不上，因为根节点为空，所以直接返回true
        {
            //如果进来了，说明到了叶子节点，该路径走完，此时需要判断blacknum是否与ref相等
            if(blackNum != ref)
            {
                cout<<"违反规则：每条路径经过的黑色节点数量不相等"<<endl;
                return false;
            }

            return true;
        }

        if(root->_col == RED && root->_parent->_col == RED)
        {
            cout<<"违反规则：红色节点不能有红色节点作为父节点"<<endl;
            return false;
        }

        if(root->_col == BLACK)
        {
            ++blackNum;
        }
        
        //特别注意下面的递归操作，可以将整棵树的左右子树都遍历一遍，
        //当遇到一个节点走到这里，返回的是这个节点的左右孩子，作下一次（同时发生两次）的循环的root
        return Check(root->_left, blackNum, ref)
               && Check(root->_right, blackNum, ref);
    }

    


    //下面部分要对红黑树进行测试
    bool IsBalance()
    {
        //包含根节点是否为空（返回真）以及是否为黑（为红返回false）
        //为黑，我们就把红黑树最左侧的树中全部黑节点作ref（参考），最后返回check函数与其他分支的黑节点数量是否相等
        //上面用到红黑树中其中一个定义：从根节点到每一条路径叶子节点，经过的黑色节点数量是相等的
        if(_root == nullptr)
        {
            return true;
        }

        if(_root->_col != BLACK)
        {
            return false;
        }

        int ref = 0;
        Node *left = _root;
        while(left)//循环找到最左侧黑色节点的数量
        {
            if(left->_col == BLACK)
            {
                ++ref;
            }

            left = left->_left;
        }

        return Check(_root, 0, ref);//根节点，黑色节点数量，最左侧路径黑色节点数量
    }

};

RBTree.cc

//测试代码

#include"RBTree.hpp"
// 6
void test01()
{
    RBTree<int,int> tree;
    int a[10] = {1,2,3,4,5,6,7,8,9,10};
    for(auto e : a)
    {
        tree.Insert(make_pair(e,e));
    }

    tree.Inorder();
    tree.IsBalance();
}

void tsest02()
{
    RBTree<int,int> tree01;
    srand(time(0));//设置随机数种子
    //搞个随机数组
    for(int i = 0; i < 1000; i++)
    {
        int val = rand();
        tree01.Insert(make_pair(val,val));
    }
   
    tree01.Inorder();
    tree01.IsBalance();
}

int main()
{
   //test01();
   tsest02();

    return 0;
}