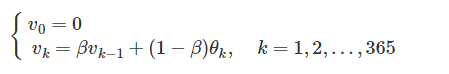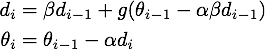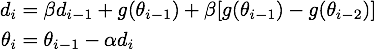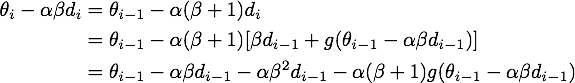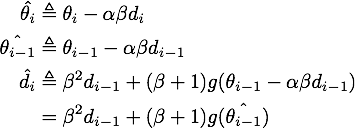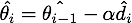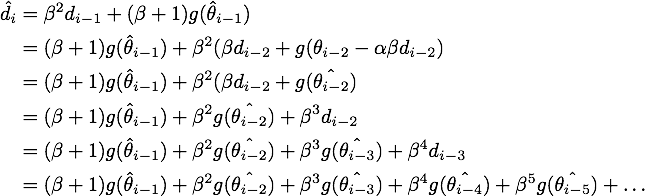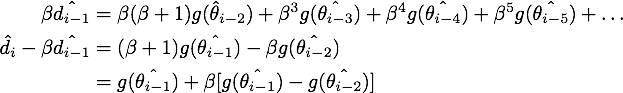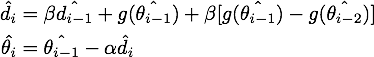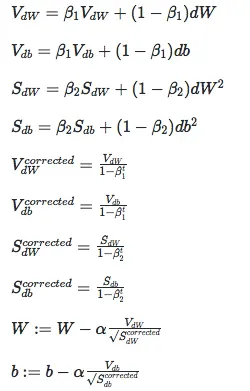机器学习中有很多优化算法,下面对这些优化算法写一些自己的理解。
-
梯度下降法(Gradient Descent)
梯度下降法是最早接触的优化算法,也是应用最广泛的优化算法,梯度具有两个重要的性质:
1. 梯度方向是函数值最速上升方向,那么负梯度方向是函数值最速下降方向
2. 如果某点的梯度不为0,则必与该点的等值面垂直。
该文章是这样理解的:
我按照梯度的定义解释一下








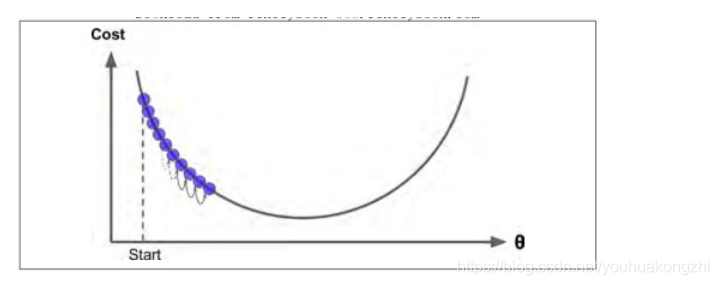
步长的选择也很有技巧,如果步长(学习率)太小,必须经过多次迭代,算法才能收敛,这是非常耗时的。如下图所示:
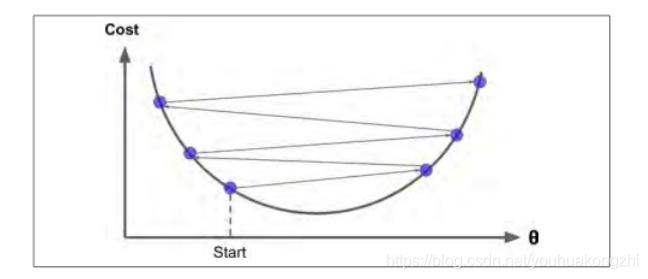
如果学习率太大,你将跳过最低点,到达山谷的另一面,可能下一次的值比上一次还要大。这可能使的算法是发散的,函数值变得越来越大,永远不可能找到一个好的答案
梯度下降(批量梯度)中每一步计算时都包含了整个训练集 ,每一次训练过程都使用所有的的训练数据。因此,在大数据集上,其会变得相当的慢( 但是我们接下来将会介绍更快的梯度下降算法) 。然而,梯度下降的运算规模和特征的数量成正比。训练一个数千数量特征的线性回归模型使用*梯度下降要比使用正态方程快的多。
梯度下降法可以有两种其他的版本:随机梯度下降法(SGD)和小批量梯度下降法 (Mini-batch-Gradient-Descent)
-
随机梯度下降法(Stochastic Gradient Descent)
由于梯度下降法每次计算时包含整个数据集,会影响计算的速度,与其完全相反的随机梯度下降(SGD),在每一步的梯度计算上只随机选取训练集中的一个样本。
由于它的随机性,与批量梯度下降相比,其呈现出更多的不规律性:它到达最小值不是平缓的下降,损失函数会忽高忽低,只是在大体上呈下降趋势。随着时间的推移,它会非常的靠近最小值,但是它不会停止在一个值上,它会一直在这个值附近摆动。因此,当算法停止的时候,最后的参数还不错,但不是最优值。
当损失函数很不规则时,随机梯度下降算法能够跳过局部最小值。虽然随机性可以很好的跳过局部最优值,但同时它却不能达到最小值。解决这个难题的一个办法是逐渐降低学习率。 开始时,走的每一步较大( 这有助于快速前进同时跳过局部最小
值) ,然后变得越来越小,从而使算法到达全局最小值。 这个过程被称为模拟退火.
-
小批量梯度下降法 (Mini-batch-Gradient-Descent)(常用)
批量梯度使用整个训练集,随机梯度时候用仅仅一个实例,在小批量梯度下降中,它则使用一个随机的小型实例集(m个实例,1<m<n)。它比随机梯度的主要优点在于你可以通过矩阵运算的硬件优化得到一个较好的训练表现.小批量梯度下降在参数空间上的表现比随机梯度下降要好的多,尤其在有大量的小型实例集时。作为结果,小批量梯度下降会比随机梯度更靠近最小值。但是,另一方面,它有可能陷在局部最小值中。
-
动量梯度下降法(Gradient descent with Momentum)
参考:https://www.cnblogs.com/jiaxblog/p/9695042.html
Momentum算法又叫做冲量算法,其迭代更新公式如下:
一般的梯度下降法的更新公式为



光看上面的公式有些抽象,我们先介绍一下指数加权平均,再回过头来看这个公式,会容易理解得多。
指数加权平均
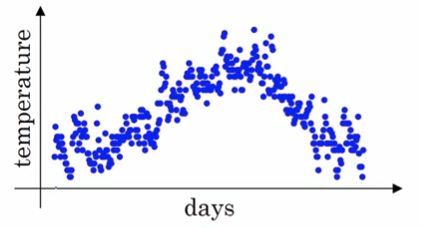
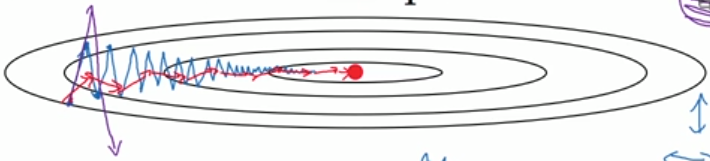
假设我们有一年365天的气温数据
这些数据有些杂乱,我们想画一条曲线,用来表征这一年气温的变化趋势,那么我们需要把数据做一次平滑处理。最常见的方法是用一个滑动窗口滑过各个数据点,计算窗口的平均值,从而得到数据的滑动平均值。但除此之外,我们还可以使用指数加权平均来对数据做平滑。其公式如下:
v就是指数加权平均值,也就是平滑后的气温。β的典型值是0.9,平滑后的曲线如下图所示:
其中,
当

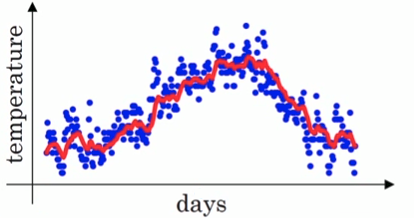
下面的图中,紫色的线就是没有做修正的结果,修正之后就是绿色曲线。二者在前面几个数据点之间相差较大,后面则基本重合了。
回看Momentum算法
现在再回过头来看Momentum算法的迭代更新公式:
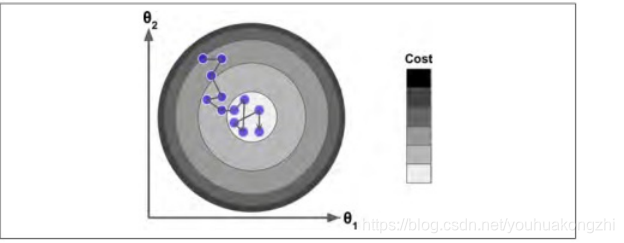
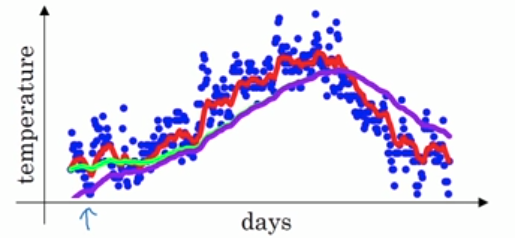
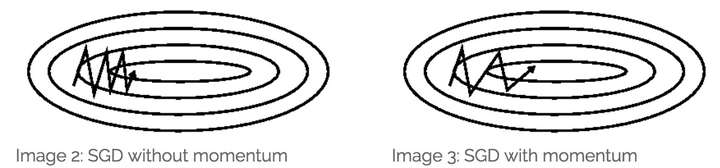
针对目标函数是上图这种形式,小批量梯度下降法(梯度下降法)的迭代轨迹如上图蓝色曲线所示,在收敛过程中产生了震荡,减慢了迭代的速度,我们观察这些震荡,在纵轴上是对称的,上下几乎可以相互抵消,也就是说如果直接沿着横轴方向迭代,收敛速度可以加快。那怎么抵消这些震荡呢?就用到上面的指数加权平均算法,指数加权平均的思想是现在的梯度方向和之间的梯度有指数加权的关系,也就是弱化了在


-
Nesterov 加速梯度(( Nesterov Accelerated Gradient,NAG)
参考:https://blog.csdn.net/google19890102/article/details/69942970
https://baijiahao.baidu.com/s?id=1613121229156499765&wfr=spider&for=pc
球从山上滚下的时候,盲目地沿着斜率方向,往往并不能令人满意。我们希望有一个智能的球,这个球能够知道它将要去哪,以至于在重新遇到斜率上升时能够知道减速。
Nesterov加速梯度下降法(Nesterov accelerated gradient,NAG)是一种能够给动量项这样的预知能力的方法。我们知道,我们利用动量项


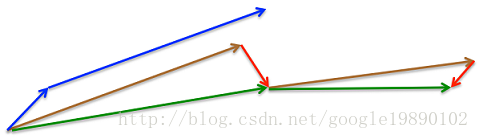
图3:Nesterov更新(来源:G. Hinton的课程6c)
Momentum梯度法首先计算的是当前的梯度(图中的小蓝色向量)然后沿着更新的累积梯度的方向来一个大的跳跃(图中大蓝色向量),而NAG梯度法首先沿着先前的累积梯度方向(棕色向量)实现一个大的跳跃,然后加上一个小的按照动量梯度法计算的当前梯度(上图红色向量)进行修正得到上图绿色的向量。此处我抛出一个问题,上图为什么画了两个三角形?如果能理解第二个矢量三解形的意义,才能正在理解NAG。注意第二个矢量三角形的棕色向量与前一个的绿色向量方向一致,因为上一个矢量三角形的结果是绿色向量,而棕色代表的是先前的累积梯度,方向就应该和绿色的一样。然后,再加上当前按照动量梯度法计算出的梯度,就得到第二个三角形的绿色向量。
我们先给出类似生活体验的通俗的解释:我们要让算法要前瞻性,提前看到前方的地形梯度,如果前面的梯度比当前位置的梯度大,那我就可以把步子迈得比原来大一些,如果前面的梯度比现在的梯度小,那我就可以把步子迈得小一些。这个大一些、小一些,都是相对于原来不看前方梯度、只看当前位置梯度的情况来说的。
下面转自知乎上的解释,讲解的非常好:https://zhuanlan.zhihu.com/p/22810533
作为一个调参狗,每天用着深度学习框架提供的各种优化算法如Momentum、AdaDelta、Adam等,却对其中的原理不甚清楚,这样和一条咸鱼有什么分别!(误)但是我又懒得花太多时间去看每个优化算法的原始论文,幸运的是,网上的大神早就已经帮人总结好了:《An overview of gradient descent optimization algorithms》,看完了这篇文章,总算可以说对自己平时用的工具有一个大概的了解啦!
文章的内容包括了Momentum、Nesterov Accelerated Gradient、AdaGrad、AdaDelta和Adam,在这么多个优化算法里面,一个妖艳的贱货(划去)成功地引起了我的注意——Nesterov Accelerated Gradient,简称NAG。原因不仅仅是它名字比别人长,而且还带了个逼格很高、一听就像是个数学家的人名,还因为,它仅仅是在Momentum算法的基础上做了一点微小的工作,形式上发生了一点看似无关痛痒的改变,却能够显著地提高优化效果。为此我折腾了一个晚上,终于扒开了它神秘的面纱……(主要是我推导公式太慢了……)
话不多说,进入正题,首先简要介绍一下Momentum和NAG,但是本文无耻地假设你已经懂了Momentum算法,如果不懂的话,强烈推荐这篇专栏:《路遥知马力——Momentum - 无痛的机器学习 - 知乎专栏》,本文的实验代码也是在这篇专栏的基础上改的。
Momentum改进自SGD算法,让每一次的参数更新方向不仅仅取决于当前位置的梯度,还受到上一次参数更新方向的影响:
公式1,Momentum的数学形式
其中,![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD1kX2k%3D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD1kXyU3QmktMSU3RA%3D%3D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD1nJTI4JTVDdGhldGElMjk%3D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUN0aGV0YQ%3D%3D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNiZXRh)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNhbHBoYQ%3D%3D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNhbHBoYQ%3D%3D%5Cbeta+d_%7Bi-1%7D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNhbHBoYQ%3D%3D+g%28%5Ctheta_%7Bi-1%7D%29)
所以Momentum的想法很简单,就是多更新一部分上一次迭代的更新量,来平滑这一次迭代的梯度。从物理的角度上解释,就像是一个小球滚落的时候会受到自身历史动量的影响,所以才叫动量(Momentum)算法。这样做直接的效果就是使得梯度下降的的时候转弯掉头的幅度不那么大了,于是就能够更加平稳、快速地冲向局部最小点:
图片引自《 An overview of gradient descent optimization algorithms》
然后NAG就对Momentum说:“既然我都知道我这一次一定会走![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNhbHBoYQ%3D%3D%5Cbeta+d_%7Bi-1%7D) 的量,那么我何必还用现在这个位置的梯度呢?我直接先走到
的量,那么我何必还用现在这个位置的梯度呢?我直接先走到![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNhbHBoYQ%3D%3D%5Cbeta+d_%7Bi-1%7D) 之后的地方,然后再根据那里的梯度再前进一下,岂不美哉?”所以就有了下面的公式:
之后的地方,然后再根据那里的梯度再前进一下,岂不美哉?”所以就有了下面的公式:
公式2,NAG的原始形式
对上面红色字体的解释:
Momentum 的迭代公式为: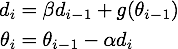
在一次迭代中总的参数更新量包含两个部分,第一个是由上次的更新量得到的![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNhbHBoYQ%3D%3D%5Cbeta+d_%7Bi-1%7D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNhbHBoYQ%3D%3D+g%28%5Ctheta_%7Bi-1%7D%29)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNhbHBoYQ%3D%3D%5Cbeta+d_%7Bi-1%7D)


![[\theta_{i-1}-\alpha \beta d_{i-1}]](/image/aHR0cHM6Ly9wcml2YXRlLmNvZGVjb2dzLmNvbS9naWYubGF0ZXg%2FJTVDZHBpJTdCMjAwJTdEJTIwJTVCJTVDdGhldGFfJTdCaS0xJTdELSU1Q2FscGhhJTIwJTVDYmV0YSUyMGRfJTdCaS0xJTdEJTVE)


![[\theta_{i-1}-\alpha \beta d_{i-1}]](/image/aHR0cHM6Ly9wcml2YXRlLmNvZGVjb2dzLmNvbS9naWYubGF0ZXg%2FJTVDZHBpJTdCMjAwJTdEJTIwJTVCJTVDdGhldGFfJTdCaS0xJTdELSU1Q2FscGhhJTIwJTVDYmV0YSUyMGRfJTdCaS0xJTdEJTVE)
跟上面Momentum公式的唯一区别在于,梯度不是根据当前参数位置![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUN0aGV0YQ%3D%3D_%7Bi-1%7D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUN0aGV0YQ%3D%3D_%7Bi-1%7D+-+%5Calpha%5Cbeta+d_%7Bi-1%7D)
对于这个改动,很多文章给出的解释是,能够让算法提前看到前方的地形梯度,如果前面的梯度比当前位置的梯度大,那我就可以把步子迈得比原来大一些,如果前面的梯度比现在的梯度小,那我就可以把步子迈得小一些。这个大一些、小一些,都是相对于原来不看前方梯度、只看当前位置梯度的情况来说的。
但是我个人对这个解释不甚满意。你说你可以提前看到,但是我下次到了那里之后不也照样看到了吗?最多比你落后一次迭代的时间,真的会造成非常大的差别?可是实验结果就是表明,NAG收敛的速度比Momentum要快:
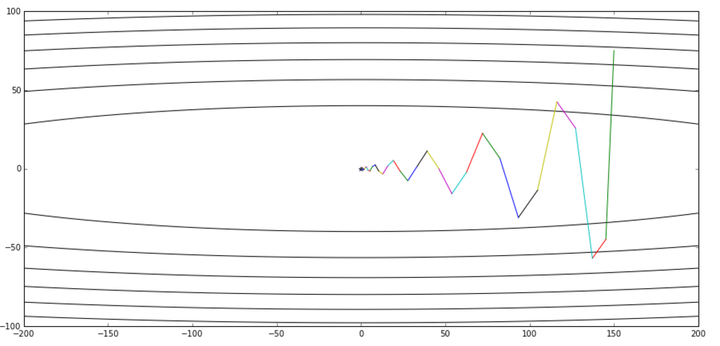
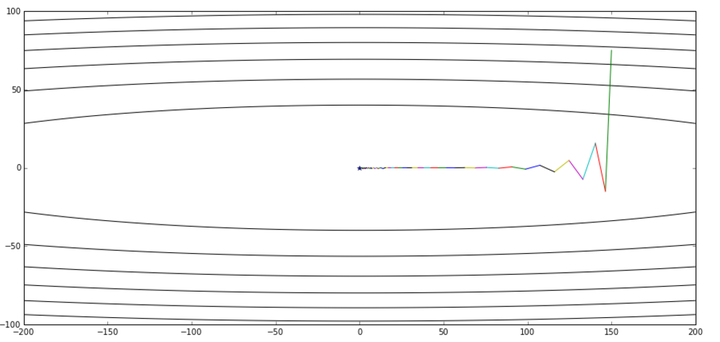
图片引自《 路遥知马力——Momentum - 无痛的机器学习 - 知乎专栏》,上图是Momentum的优化轨迹,下图是NAG的优化轨迹
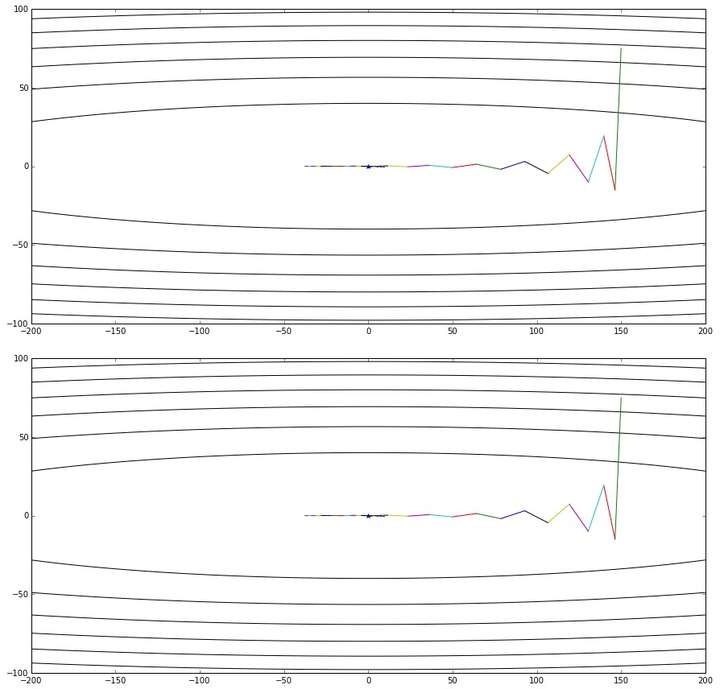
为了从另一个角度更加深入地理解这个算法,我们可以对NAG原来的更新公式进行变换,得到这样的等效形式(具体推导过程放在最后啦):
公式3,NAG的等效形式
这个NAG的等效形式与Momentum的区别在于,本次更新方向多加了一个![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNiZXRh%5Bg%28%5Ctheta_%7Bi-1%7D%29+-+g%28%5Ctheta_%7Bi-2%7D%29%5D)
关于二阶导数的理解:由于




![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNiZXRh%5Bg%28%5Ctheta_%7Bi-1%7D%29+-+g%28%5Ctheta_%7Bi-2%7D%29%5D)
那么,变换后的形式真的与NAG的原始形式等效么?在给出数学推导之前,先让我用实验来说明吧:
上图是公式3给出的优化轨迹,下图是公式2给出的优化轨迹——完全一样
实验代码放在Github,修改自《路遥知马力——Momentum - 无痛的机器学习 - 知乎专栏》的实验代码。有兴趣的读者可以多跑几个起始点+学习率+衰减率的超参数组合,无论如何两个算法给出的轨迹都会是一样的。
最后给出NAG的原始形式到等效形式的推导。由
可得
记
上式代入上上式,就得到了NAG等效形式的第二个式子:
对![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNoYXQlN0JkX2klN0Q%3D)
于是我们可以写出![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNoYXQlN0JkXyU3QmktMSU3RCU3RA%3D%3D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNoYXQlN0JkX2klN0Q%3D)
![[公式]](/image/aHR0cHM6Ly93d3cuemhpaHUuY29tL2VxdWF0aW9uP3RleD0lNUNiZXRh%5Chat%7Bd_%7Bi-1%7D%7D)
最终我们就得到了NAG的等效形式:
结论:在原始形式中,Nesterov Accelerated Gradient(NAG)算法相对于Momentum的改进在于,以“向前看”看到的梯度而不是当前位置梯度去更新。经过变换之后的等效形式中,NAG算法相对于Momentum多了一个本次梯度相对上次梯度的变化量,这个变化量本质上是对目标函数二阶导的近似。由于利用了二阶导的信息,NAG算法才会比Momentum具有更快的收敛速度。
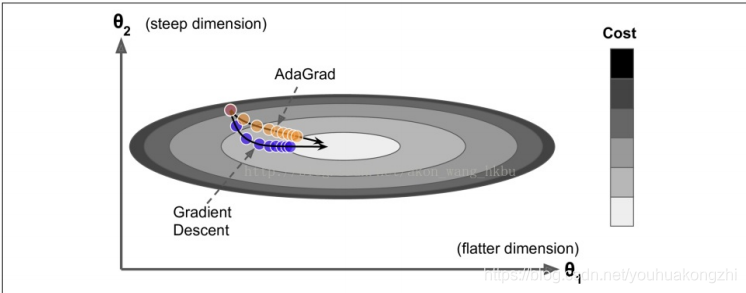
来自:https://blog.csdn.net/SIGAI_CSDN/article/details/81979837
简而言之,这种算法会降低学习速度,但对于陡峭的尺寸,其速度要快于具有温和的斜率的尺寸。 这被称为自适应学习率。 它有助于将更新的结果更直接地指向全局最优 。 另一个好处是它不需要那么多的去调整学习率超参数 η。
对于简单的二次问题,AdaGrad 经常表现良好,但不幸的是,在训练神经网络时,它经常停止得太早。 学习率被缩减得太多,以至于在达到全局最优之前,算法完全停止。 所以,即使TensorFlow 有一个 AdagradOptimizer ,你也不应该用它来训练深度神经网络( 虽然对线性回归这样简单的任务可能是有效的)
-
RMSprop算法(Root Mean Square Prop)
尽管 AdaGrad 的速度变慢了一点,并且从未收敛到全局最优,但是 RMSProp 算法通过仅累积最近迭代( 而不是从训练开始以来的所有梯度) 的梯度来修正这个问题。
还是观察上面的图
如果纵坐标是b,横坐标是w,梯度方向在b方向上的投影大,在w方向上的投影小,故db>dw,
RMSprop公式如下所示:
由于


比
大一些,因此
更小一些,就减小的b方向上的步长,加快了w方向上的步长。为什么有



除了非常简单的问题,这个优化器几乎总是比 AdaGrad 执行得更好。 它通常也比动量优化和Nesterov 加速梯度表现更好。 事实上,这是许多研究人员首选的优化算法,直到 Adam 优化出现。
-
Adam(Adaptive Moment Estimation)
Adam,代表自适应矩估计,结合了动量优化和 RMSProp 的思想:就像动量优化一样,它追踪过去梯度的指数衰减平均值,就像 RMSProp 一样,它跟踪过去平方梯度的指数衰减平均值。
Adam是Moment和RMSprop的结合,Adam的公式如下:

Adam的优点
- 计算高效,方便实现,内存使用也很少。
- 更新步长和梯度大小无关,只和alpha、beta_1、beta_2有关系。并且由它们决定步长的理论上限。
- 对目标函数没有平稳要求,即loss function可以随着时间变化
- 能较好的处理噪音样本,并且天然具有退火效果
- 能较好处理稀疏梯度,即梯度在很多step处都是0的情况
迄今为止所讨论的所有优化技术都只依赖于一阶偏导数( 雅可比矩阵) 。 优化文献包含基于二阶偏导数( 海森矩阵) 的惊人算法。 不幸的是,这些算法很难应用于深度神经网络,因为每个输出有 n ^ 2 个海森值( 其中 n 是参数的数量) ,而不是每个输出只有 n 个雅克比值。由于 DNN 通常具有数以万计的参数,二阶优化算法通常甚至不适合内存,甚至在他们这样做时,计算海森矩阵也是太慢了。
优化算法还没更新完,等到碰到会继续更新!