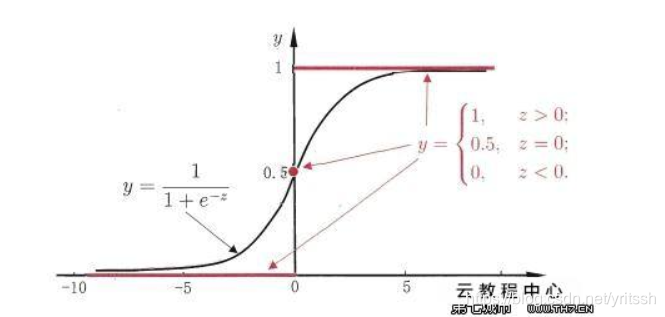
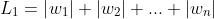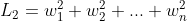接着上篇文章(逻辑回归_斜杆小刘的博客-CSDN博客_逻辑回归损失函数可以用mse吗),继续分析逻辑回归。此文主要分析逻辑回归的正则化问题。首先继续给出sigmoid函数和它对应的图像:
如果 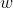
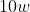
- 首先,它不会改变分类结果,因为要想改变分类结果
必须反向 ,就是说变为
或
(
是正数)。观察sigmoid函数,直接影响的就是
这项,会使它增大(或缩小),再图像中体现为,点会沿着
的正方向(负方向)移动,最终造成的结果就是,使得
的值更趋向于1(或0),使得最终的分类结果过硬,显然这不是我们想要的结果,因为实际我们是通过设定一个阈值来进行分类的,要是
预测出的最终的结果都是趋近于1或0,我们再调整阈值进行分类的时候就不好调了。
- 实际中我们训练的数据都是有噪声的,也就是说
可以分为真实信息和噪声两部分,即
,其中
表示真实信息部分,
表示噪声部分。如果
变大,看似真实信息和噪声的是同时放大的,但实际是真实信息是会冗余的,而噪声不会, 造成的结果就是信噪比降低,显然这也不是我们想要的结果。
- 如果
越小,训练集和测试集的差异就小。造成训练集和测试集有差异的本质问题是数据不一样,即
不一样,而要想将训练集和测试集的差异变小,就要忽略这些数据集的影响,考虑一个极端的例子,如果
等于 0,那么,不管你输入的数据是什么数据,
恒成立,这样的话,训练集和测试集的差异就没有了。所以
越小,训练集和测试集的差异就越小,说明模型的推广能力就越好。
正则项
接下来我们引入正则项,在实际中,逻辑回归的损失函数包括两部分,如下:
为了方便分析,我们就直接看 ![[y_{i}*logf_{i}+(1-y_{i})*log(1-f_{i})] + \lambda \left \| w \right \|](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvNzlmNTQ4ZDExZTg5YTY0YjkyMDQ4NzFmYjNlOWQ4ZGIuZ2lm)
观察损失函数左边部分![[y_{i}*logf_{i}+(1-y_{i})*log(1-f_{i})]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvYWYxZWRlNTY3ZDQ2M2E2NTI1NGMyNWQ0YjY0NzJlOWQuZ2lm)
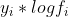
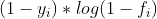
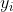
= 0 时,
,可以通过不断增大
来使得
无限逼近 0,使得损失函数无限变小
= 1时,
,可以通过不断增大
来使得
无限逼近 1,使得损失函数无限变小
从上面两种情况可知,我们可以无限的增大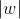
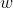
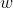
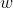
L1:一般会用于降维,有特征筛选的作用(真实场景中常用L1正则)
L2:各个维度权重普遍变小
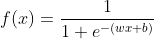
![d_{KL} = -\frac{1}{n}\sum_{i=1}^{n}([y_{i}*logf_{i}+(1-y_{i})*log(1-f_{i})] + \lambda \left \| w \right \|)](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvNWU3MmM5OWU5MjgzYjkzMzRmOGM0NjE3MzA0ZjBkNjguZ2lm)