torch.optim
torch.optim是一个实现了各种优化算法的库。大部分常用的方法得到支持,并且接口具备足够的通用性,使得未来能够集成更加复杂的方法。
如何使用optimizer
为了使用torch.optim,你需要构建一个optimizer对象。这个对象能够保持当前参数状态并基于计算得到的梯度进行参数更新。
构建
为了构建一个Optimizer,你需要给它一个包含了需要优化的参数(必须都是Variable对象)的iterable。然后,你可以设置optimizer的参数选项,比如学习率,权重衰减,等等。
例子:
optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.9)
optimizer = optim.Adam([var1, var2], lr = 0.0001)
为每个参数单独设置选项
Optimizer也支持为每个参数单独设置选项。若想这么做,不要直接传入Variable的iterable,而是传入dict的iterable。每一个dict都分别定 义了一组参数,并且包含一个param键,这个键对应参数的列表。其他的键应该optimizer所接受的其他参数的关键字相匹配,并且会被用于对这组参数的 优化。
注意:
你仍然能够传递选项作为关键字参数。在未重写这些选项的组中,它们会被用作默认值。当你只想改动一个参数组的选项,但其他参数组的选项不变时,这是 非常有用的。
例如,当我们想指定每一层的学习率时,这是非常有用的:
optim.SGD([
{'params': model.base.parameters()},
{'params': model.classifier.parameters(), 'lr': 1e-3}
], lr=1e-2, momentum=0.9)
这意味着model.base的参数将会使用1e-2的学习率,model.classifier的参数将会使用1e-3的学习率,并且0.9的momentum将会被用于所 有的参数。
进行单次优化
所有的optimizer都实现了step()方法,这个方法会更新所有的参数。它能按两种方式来使用:
optimizer.step()
这是大多数optimizer所支持的简化版本。一旦梯度被如backward()之类的函数计算好后,我们就可以调用这个函数。
例子
for input, target in dataset:
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
optimizer.step()
optimizer.step(closure)
一些优化算法例如Conjugate Gradient和LBFGS需要重复多次计算函数,因此你需要传入一个闭包去允许它们重新计算你的模型。这个闭包应当清空梯度, 计算损失,然后返回。
例子:
for input, target in dataset:
def closure():
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
return loss
optimizer.step(closure)
class torch.optim.Optimizer(params, defaults)
Base class for all optimizers.
参数:
- params (iterable) ——
Variable或者dict的iterable。指定了什么参数应当被优化。 - defaults —— (dict):包含了优化选项默认值的字典(一个参数组没有指定的参数选项将会使用默认值)。
load_state_dict(state_dict)
加载optimizer状态
参数:
state_dict (dict) —— optimizer的状态。应当是一个调用state_dict()所返回的对象。
state_dict()
以dict返回optimizer的状态。
它包含两项。
- state - 一个保存了当前优化状态的dict。optimizer的类别不同,state的内容也会不同。
- param_groups - 一个包含了全部参数组的dict。
step(closure)
进行单次优化 (参数更新).
参数:
- closure (
callable) – 一个重新评价模型并返回loss的闭包,对于大多数参数来说是可选的。
zero_grad() [source]
清空所有被优化过的Variable的梯度
1 torch.optim.SGD
class torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
功能:
可实现SGD优化算法,带动量SGD优化算法,带NAG(Nesterov accelerated gradient)动量SGD优化算法,并且均可拥有weight_decay项。
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (
float) – 学习率 - momentum (
float, 可选) – 动量因子(默认:0) - weight_decay (
float, 可选) – 权重衰减(L2惩罚)(默认:0) - dampening (
float, 可选) – 动量的抑制因子(默认:0)在源码中是这样用的:buf.mul_(momentum).add_(1 - dampening, d_p),值得注意的是,若采用nesterov,dampening必须为 0. - nesterov (
bool, 可选) – 使用Nesterov动量(默认:False)
注意事项:
pytroch中使用SGD十分需要注意的是,更新公式与其他框架略有不同!
pytorch中是这样的:
v
=
ρ
∗
v
+
g
p
=
p
−
l
r
∗
v
=
p
−
l
r
∗
ρ
∗
v
−
l
r
∗
g
v=ρ∗v+g\\ p=p−lr∗v = p - lr∗ρ∗v - lr∗g
v=ρ∗v+gp=p−lr∗v=p−lr∗ρ∗v−lr∗g
其他框架:
v
=
ρ
∗
v
+
l
r
∗
g
p
=
p
−
v
=
p
−
ρ
∗
v
−
l
r
∗
g
v=ρ∗v+lr∗g\\ p=p−v = p - ρ∗v - lr∗g
v=ρ∗v+lr∗gp=p−v=p−ρ∗v−lr∗g
ρ是动量,v是速率,g是梯度,p是参数,其实差别就是在ρ∗v这一项,pytorch中将此项也乘了一个学习率。
手写sgd
def sgd_update(parameters, lr):
for param in parameters:
param.data = param.data - lr * param.grad.data
def sgd_momentum(parameters, vs, lr, gamma):
for param, v in zip(parameters, vs):
v[:] = gamma * v + lr * param.grad.data
param.data = param.data - v
loss.backward()
sgd_momentum(net.parameters(), vs, 1e-2, 0.9) # 使用的动量参数为 0.9,学习率 0.01
2 torch.optim.ASGD
class torch.optim.ASGD(params, lr=0.01, lambd=0.0001, alpha=0.75, t0=1000000.0, weight_decay=0)
功能:
ASGD也成为SAG,均表示随机平均梯度下降(Averaged Stochastic Gradient Descent),简单地说ASGD就是用空间换时间的一种SGD,详细可参看论文:http://riejohnson.com/rie/stograd_nips.pdf
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (
float, 可选) – (默认:1e-2)初始学习率,可按需随着训练过程不断调整学习率 - lambd (
float, 可选) – 衰减项(默认:1e-4) - alpha (
float, 可选) – eta更新的指数(默认:0.75) - t0 (
float, 可选) – 指明在哪一次开始平均化(默认:1e6) - weight_decay (
float, 可选) – 权重衰减(L2惩罚)(默认: 0)
3 torch.optim.Rprop
class torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))
功能:
实现Rprop优化方法(弹性反向传播),优化方法原文《Martin Riedmiller und Heinrich Braun: Rprop - A Fast Adaptive Learning Algorithm. Proceedings of the International Symposium on Computer and Information Science VII, 1992》
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (
float, 可选) – 学习率(默认:1e-2) - etas (Tuple[
float,float], 可选) – 一对(etaminus,etaplis), 它们分别是乘法的增加和减小的因子(默认:0.5,1.2) - step_sizes (Tuple[
float,float], 可选) – 允许的一对最小和最大的步长(默认:1e-6,50)
该优化方法适用于full-batch,不适用于mini-batch,因而在min-batch大行其道的时代里,很少见到。
4 torch.optim.Adagrad
classs torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0)
功能:
实现Adagrad优化方法(Adaptive Gradient),Adagrad是一种自适应优化方法,是自适应的为各个参数分配不同的学习率。这个学习率的变化,会受到梯度的大小和迭代次数的影响。梯度越大,学习率越小;梯度越小,学习率越大。缺点是训练后期,学习率过小,因为Adagrad累加之前所有的梯度平方作为分母。
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (
float, 可选) – 学习率(默认: 1e-2) - lr_decay (
float, 可选) – 学习率衰减(默认: 0) - weight_decay (
float, 可选) – 权重衰减(L2惩罚)(默认: 0)
step(closure=None)
进行单次优化 (参数更新).
参数:
- closure (
callable) – 一个重新评价模型并返回loss的闭包,对于大多数参数来说是可选的。
手写Adagrad
def sgd_adagrad(parameters, sqrs, lr):
eps = 1e-10
for param, sqr in zip(parameters, sqrs):
sqr[:] = sqr + param.grad.data ** 2
div = lr / torch.sqrt(sqr + eps) * param.grad.data
param.data = param.data - div
# 在循环中更新参数
sgd_adagrad(net.parameters(), sqrs, 1e-2) # 学习率设为 0.01
5 torch.optim.Adadelta
class torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)
功能:
实现Adadelta优化方法。Adadelta是Adagrad的改进。Adadelta分母中采用距离当前时间点比较近的累计项,这可以避免在训练后期,学习率过小。
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- rho (
float, 可选) – 用于计算平方梯度的运行平均值的系数(默认:0.9) - eps (
float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-6) - lr (
float, 可选) – 在delta被应用到参数更新之前对它缩放的系数(默认:1.0) - weight_decay (
float, 可选) – 权重衰减(L2惩罚)(默认: 0)
step(closure=None)
进行单次优化 (参数更新).
参数:
- closure (
callable) – 一个重新评价模型并返回loss的闭包,对于大多数参数来说是可选的。
手写Adadelta
def adadelta(parameters, sqrs, deltas, rho):
eps = 1e-6
for param, sqr, delta in zip(parameters, sqrs, deltas):
sqr[:] = rho * sqr + (1 - rho) * param.grad.data ** 2
cur_delta = torch.sqrt(delta + eps) / torch.sqrt(sqr + eps) * param.grad.data
delta[:] = rho * delta + (1 - rho) * cur_delta ** 2
param.data = param.data - cur_delta
# 循环中更新参数
adadelta(net.parameters(), sqrs, deltas, 0.9) # rho 设置为 0.9
6 torch.optim.RMSprop
class torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
功能:
实现RMSprop优化方法(Hinton提出),RMS是均方根(root meam square)的意思。RMSprop和Adadelta一样,也是对Adagrad的一种改进。RMSprop采用均方根作为分母,可缓解Adagrad学习率下降较快的问题。并且引入均方根,可以减少摆动.
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (
float, 可选) – 学习率(默认:1e-2) - momentum (
float, 可选) – 动量因子(默认:0) - alpha (
float, 可选) – 平滑常数(默认:0.99) - eps (
float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8) - centered (
bool, 可选) – 如果为True,计算中心化的RMSProp,并且用它的方差预测值对梯度进行归一化 - weight_decay (
float, 可选) – 权重衰减(L2惩罚)(默认: 0)
手写rmsprop
def rmsprop(parameters, sqrs, lr, alpha):
eps = 1e-10
for param, sqr in zip(parameters, sqrs):
sqr[:] = alpha * sqr + (1 - alpha) * param.grad.data ** 2
div = lr / torch.sqrt(sqr + eps) * param.grad.data
param.data = param.data - div
loss.backward()
rmsprop(net.parameters(), sqrs, 1e-3, 0.9) # 学习率设为 0.001,alpha 设为 0.9
7 torch.optim.Adam(AMSGrad)
class torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
功能:
实现Adam(Adaptive Moment Estimation))优化方法。Adam是一种自适应学习率的优化方法,Adam利用梯度的一阶矩估计和二阶矩估计动态的调整学习率。吴老师课上说过,Adam是结合了Momentum和RMSprop,并进行了偏差修正。
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (
float, 可选) – 学习率(默认:1e-3) - betas (Tuple[
float,float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999) - eps (
float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8) - weight_decay (
float, 可选) – 权重衰减(L2惩罚)(默认: 0) - amsgrad - 是否采用AMSGrad优化方法,asmgrad优化方法是针对Adam的改进,通过添加额外的约束,使学习率始终为正值。(AMSGrad,ICLR-2018 Best-Pper之一,《On the convergence of Adam and Beyond》)。
手写adam
def adam(parameters, vs, sqrs, lr, t, beta1=0.9, beta2=0.999):
eps = 1e-8
for param, v, sqr in zip(parameters, vs, sqrs):
v[:] = beta1 * v + (1 - beta1) * param.grad.data
sqr[:] = beta2 * sqr + (1 - beta2) * param.grad.data ** 2
v_hat = v / (1 - beta1 ** t)
s_hat = sqr / (1 - beta2 ** t)
param.data = param.data - lr * v_hat / torch.sqrt(s_hat + eps)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)
# 初始化梯度平方项和动量项
sqrs = []
vs = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))
vs.append(torch.zeros_like(param.data))
t = 1
# 开始训练
losses = []
idx = 0
for e in range(5):
train_loss = 0
for im, label in train_data:
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
adam(net.parameters(), vs, sqrs, 1e-3, t) # 学习率设为 0.001
t += 1
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
8 torch.optim.Adamax
class torch.optim.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
功能:
实现Adamax优化方法。Adamax是对Adam增加了一个学习率上限的概念,所以也称之为Adamax。 Adam的一种基于无穷范数的变种
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (
float, 可选) – 学习率(默认:2e-3) - betas (Tuple[
float,float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数 - eps (
float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8) - weight_decay (
float, 可选) – 权重衰减(L2惩罚)(默认: 0)
9 torch.optim.SparseAdam
class torch.optim.SparseAdam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08)
功能:
针对稀疏张量的一种“阉割版”Adam优化方法。
only moments that show up in the gradient get updated, and only those portions of the gradient get applied to the parameters
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (
float, 可选) – 学习率(默认:1e-3) - betas (Tuple[
float,float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数 - eps (
float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
10 torch.optim.LBFGS
class torch.optim.LBFGS(params, lr=1, max_iter=20, max_eval=None, tolerance_grad=1e-05, tolerance_change=1e-09, history_size=100, line_search_fn=None)
功能:
实现L-BFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)优化方法。L-BFGS属于拟牛顿算法。L-BFGS是对BFGS的改进,特点就是节省内存。
使用注意事项:
警告
这个optimizer不支持为每个参数单独设置选项以及不支持参数组(只能有一个)
警告
目前所有的参数不得不都在同一设备上。在将来这会得到改进。
注意
这是一个内存高度密集的optimizer(它要求额外的param_bytes * (history_size + 1) 个字节)。如果它不适应内存,尝试减小history size,或者使用不同的算法。
参数:
- lr (
float) – 学习率(默认:1) - max_iter (
int) – 每一步优化的最大迭代次数(默认:20)) - max_eval (
int) – 每一步优化的最大函数评价次数(默认:max_iter * 1.25) - tolerance_grad (
float) – 一阶最优的终止容忍度(默认:1e-5) - tolerance_change (
float) – 在函数值/参数变化量上的终止容忍度(默认:1e-9) - history_size (
int) – 更新历史的大小(默认:100)
什么是参数组 /param_groups?
optimizer通过param_group来管理参数组.param_group中保存了参数组及其对应的学习率,动量等等.所以我们可以通过更改param_group['lr']的值来更改对应参数组的学习率.
下面有一个手动更改学习率的例子
# 有两个`param_group`即,len(optim.param_groups)==2
optim.SGD([
{'params': model.base.parameters()},
{'params': model.classifier.parameters(), 'lr': 1e-3}
], lr=1e-2, momentum=0.9)
#一个参数组
optim.SGD(model.parameters(), lr=1e-2, momentum=.9)
# 获得学习率
print('learning rate: {}'.format(optimizer.param_groups[0]['lr']))
print('weight decay: {}'.format(optimizer.param_groups[0]['weight_decay']))
如何调整学习率
torch.optim.lr_scheduler provides several methods to adjust the learning rate based on the number of epochs. torch.optim.lr_scheduler.ReduceLROnPlateau allows dynamic learning rate reducing based on some validation measurements.
PyTorch学习率调整策略通过torch.optim.lr_scheduler接口实现。PyTorch提供的学习率调整策略分为三大类,分别是
a. 有序调整:等间隔调整(Step),按需调整学习率(MultiStep),指数衰减调整(Exponential)和 余弦退火CosineAnnealing。
b. 自适应调整:自适应调整学习率 ReduceLROnPlateau。
c. 自定义调整:自定义调整学习率 LambdaLR。
第一类,依一定规律有序进行调整,这一类是最常用的,分别是等间隔下降(Step),按需设定下降间隔(MultiStep),指数下降(Exponential)和 CosineAnnealing。这四种方法的调整时机都是人为可控的,也是训练时常用到的。
第二类,依训练状况伺机调整,这就是 ReduceLROnPlateau 方法。该法通过监测某一指标的变化情况,当该指标不再怎么变化的时候,就是调整学习率的时机,因而属于自适应的调整。
第三类,自定义调整, Lambda。 Lambda 方法提供的调整策略十分灵活,我们可以为不同的层设定不同的学习率调整方法,这在 fine-tune 中十分有用,我们不仅可为不同的层设定不同的学习率,还可以为其设定不同的学习率调整策略,简直不能更棒!
scheduler.step()
scheduler.step()在一次循环中只能出现一次
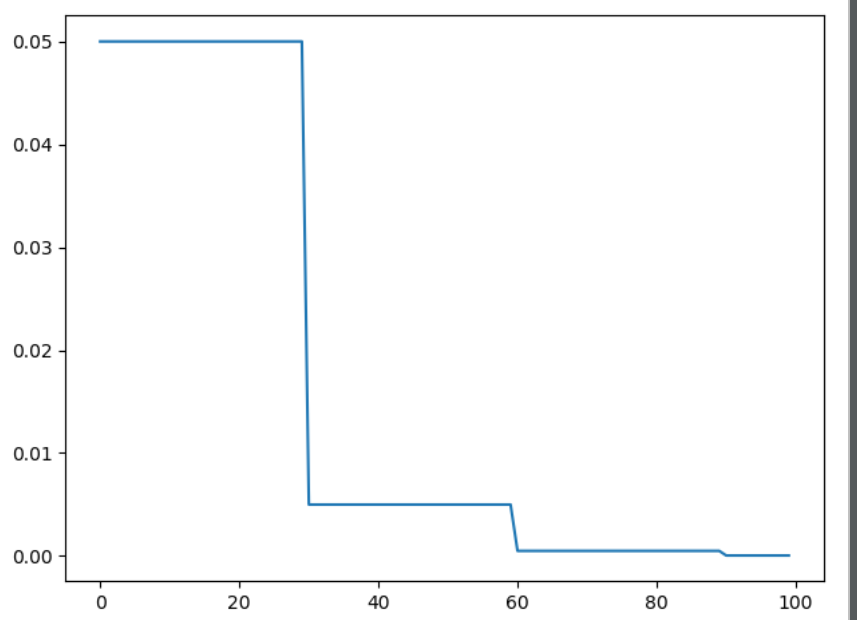
1 等间隔调整学习率 StepLR
等间隔调整学习率,调整倍数为 gamma 倍,调整间隔为 step_size。间隔单位是step。需要注意的是, step 通常是指 epoch,不要弄成 iteration 了。
torch.optim.lr_scheduler.StepLR(optimizer, step_size, gamma=0.1, last_epoch=-1)
参数:
- step_size(int) - 学习率下降间隔数,若为 30,则会在 30、 60、 90…个 step 时,将学习率调整为 lr*gamma。
- gamma(float)- 学习率调整倍数,默认为 0.1 倍,即下降 10 倍。
- last_epoch(int)- 上一个 epoch 数,这个变量用来指示学习率是否需要调整。当last_epoch 符合设定的间隔时,就会对学习率进行调整。当为-1 时,学习率设置为初始值。
import torch
import torch.optim as optim
from torch.optim import lr_scheduler
from torchvision.models import AlexNet
import matplotlib.pyplot as plt
model = AlexNet(num_classes=2)
optimizer = optim.SGD(params=model.parameters(), lr=0.05)
# lr_scheduler.StepLR()
# Assuming optimizer uses lr = 0.05 for all groups
# lr = 0.05 if epoch < 30
# lr = 0.005 if 30 <= epoch < 60
# lr = 0.0005 if 60 <= epoch < 90
scheduler = lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
plt.figure()
x = list(range(100))
y = []
for epoch in range(100):
scheduler.step()
lr = scheduler.get_lr()
print(epoch, scheduler.get_lr()[0])
y.append(scheduler.get_lr()[0])
plt.plot(x, y)
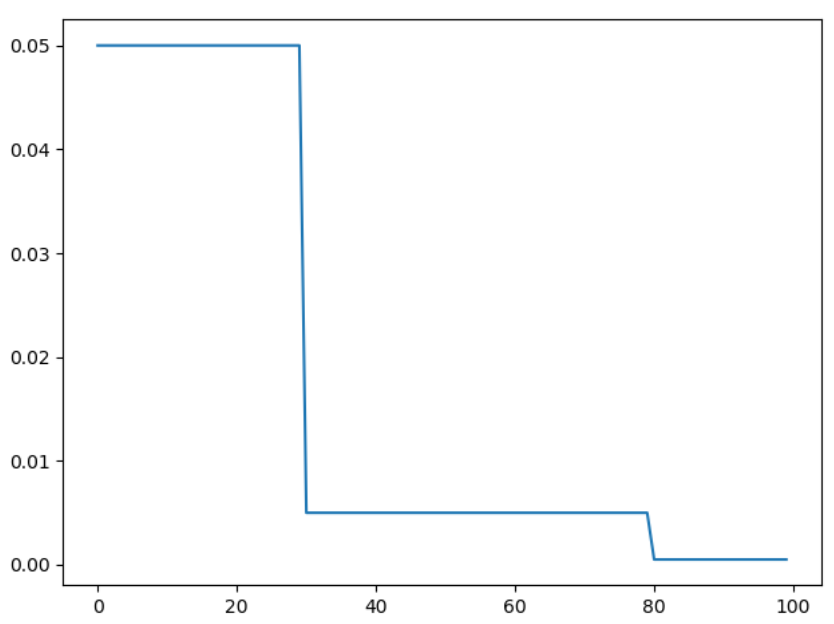
2 按需调整学习率 MultiStepLR
按设定的间隔调整学习率。这个方法适合后期调试使用,观察 loss 曲线,为每个实验定制学习率调整时机。
torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones, gamma=0.1, last_epoch=-1)
参数:
- milestones(list)- 一个 list,每一个元素代表何时调整学习率, list 元素必须是递增的。如 milestones=[30,80,120]
- gamma(float) - 学习率调整倍数,默认为 0.1 倍,即下降 10 倍。
- last_epoch(int )- 上一个 epoch 数,这个变量用来指示学习率是否需要调整。last_epoch 符合设定的间隔时,就会对学习率进行调整。当为-1 时,学习率设置为初始值。
# ---------------------------------------------------------------
# 可以指定区间
# lr_scheduler.MultiStepLR()
# Assuming optimizer uses lr = 0.05 for all groups
# lr = 0.05 if epoch < 30
# lr = 0.005 if 30 <= epoch < 80
# lr = 0.0005 if epoch >= 80
print()
plt.figure()
y.clear()
scheduler = lr_scheduler.MultiStepLR(optimizer, [30, 80], 0.1)
for epoch in range(100):
scheduler.step()
print(epoch, 'lr={:.6f}'.format(scheduler.get_lr()[0]))
y.append(scheduler.get_lr()[0])
plt.plot(x, y)
plt.show()
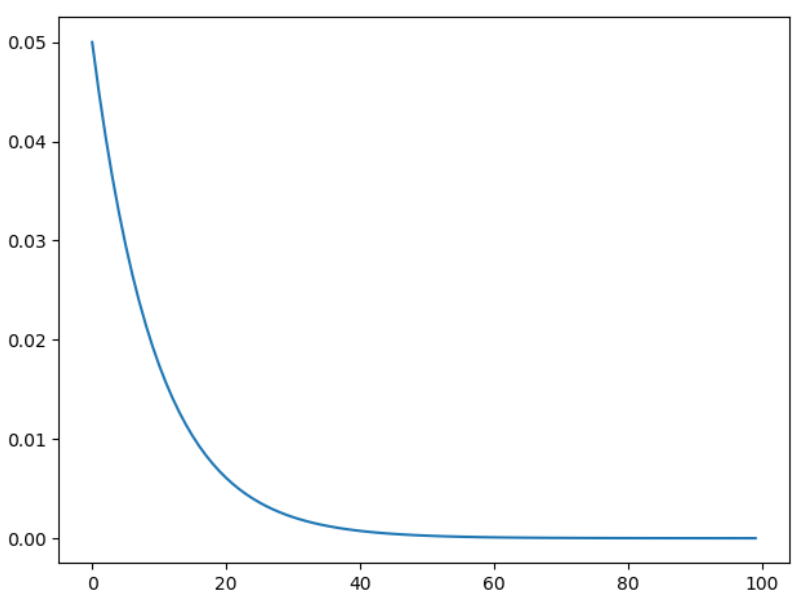
3 指数衰减调整学习率 ExponentialLR
按指数衰减调整学习率,调整公式:$ lr=lr∗gamma∗∗epoch $
torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma, last_epoch=-1)
参数:
-
gamma- 学习率调整倍数的底,指数为 epoch,即 gamma**epoch
-
last_epoch(int)- 上一个 epoch 数,这个变量用来指示学习率是否需要调整。当
last_epoch 符合设定的间隔时,就会对学习率进行调整。当为-1 时,学习率设置为初始
值。
scheduler = lr_scheduler.ExponentialLR(optimizer, gamma=0.9)
print()
plt.figure()
y.clear()
for epoch in range(100):
scheduler.step()
print(epoch, 'lr={:.6f}'.format(scheduler.get_lr()[0]))
y.append(scheduler.get_lr()[0])
plt.plot(x, y)
plt.show()
4 余弦退火调整学习率 CosineAnnealingLR
以余弦函数为周期,并在每个周期最大值时重新设置学习率。以初始学习率为最大学习率,以 2∗Tmax 为周期,在一个周期内先下降,后上升。
torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=-1)
参数:
- T_max(int)- 一次学习率周期的迭代次数,即 T_max 个 epoch 之后重新设置学习率。
- eta_min(float)- 最小学习率,即在一个周期中,学习率最小会下降到 eta_min,默认值为 0。
学习率调整公式为:
η
t
+
1
=
η
m
i
n
+
(
η
t
−
η
m
i
n
)
1
+
cos
(
T
c
u
r
+
1
T
m
a
x
π
)
1
+
cos
(
T
c
u
r
T
m
a
x
π
)
,
T
c
u
r
≠
(
2
k
+
1
)
T
m
a
x
;
η
t
+
1
=
η
t
+
(
η
m
a
x
−
η
m
i
n
)
1
−
cos
(
1
T
m
a
x
π
)
2
,
T
c
u
r
=
(
2
k
+
1
)
T
m
a
x
.
\eta_{t+1} = \eta_{min} + (\eta_t - \eta_{min})\frac{1 + \cos(\frac{T_{cur}+1}{T_{max}}\pi)}{1 + \cos(\frac{T_{cur}}{T_{max}}\pi)}, T_{cur} \neq (2k+1)T_{max};\\ \eta_{t+1} = \eta_{t} + (\eta_{max} - \eta_{min})\frac{1 - \cos(\frac{1}{T_{max}}\pi)}{2}, T_{cur} = (2k+1)T_{max}.
ηt+1=ηmin+(ηt−ηmin)1+cos(TmaxTcurπ)1+cos(TmaxTcur+1π),Tcur̸=(2k+1)Tmax;ηt+1=ηt+(ηmax−ηmin)21−cos(Tmax1π),Tcur=(2k+1)Tmax.
When last_epoch=-1, sets initial lr as lr. Notice that because the schedule is defined recursively, the learning rate can be simultaneously modified outside this scheduler by other operators. If the learning rate is set solely by this scheduler, the learning rate at each step becomes:
η
t
=
η
m
i
n
+
1
2
(
η
m
a
x
−
η
m
i
n
)
(
1
+
cos
(
T
c
u
r
T
m
a
x
π
)
)
\eta_t = \eta_{min} + \frac{1}{2}(\eta_{max} - \eta_{min})(1 + \cos(\frac{T_{cur}}{T_{max}}\pi))
ηt=ηmin+21(ηmax−ηmin)(1+cos(TmaxTcurπ))
5 根据指标调整学习率 ReduceLROnPlateau
当某指标不再变化(下降或升高),调整学习率,这是非常实用的学习率调整策略。
例如,当验证集的 loss 不再下降时,进行学习率调整;或者监测验证集的 accuracy,当accuracy 不再上升时,则调整学习率。
torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=10, verbose=False, threshold=0.0001, threshold_mode='rel', cooldown=0, min_lr=0, eps=1e-08)
参数:
-
mode(str)- 模式选择,有 min 和 max 两种模式, min 表示当指标不再降低(如监测loss), max 表示当指标不再升高(如监测 accuracy)。
-
factor(float)- 学习率调整倍数(等同于其它方法的 gamma),即学习率更新为 lr = lr * factor
-
patience(int)- 忍受该指标多少个 step 不变化,当忍无可忍时,调整学习率。
-
verbose(bool)- 是否打印学习率信息, print(‘Epoch {:5d}: reducing learning rate of group {} to {:.4e}.’.format(epoch, i, new_lr))
如果为true,则为每个更新将消息打印到stdout。默认值:false。
-
threshold_mode(str)- 选择判断指标是否达最优的模式,有两种模式, rel 和 abs。
当 threshold_mode == rel,并且 mode == max 时, dynamic_threshold = best * ( 1 +threshold );
当 threshold_mode == rel,并且 mode == min 时, dynamic_threshold = best * ( 1 -threshold );
当 threshold_mode == abs,并且 mode== max 时, dynamic_threshold = best + threshold ;
当 threshold_mode == rel,并且 mode == max 时, dynamic_threshold = best - threshold; -
threshold(float)- 配合 threshold_mode 使用。
-
cooldown(int)- “冷却时间“,当调整学习率之后,让学习率调整策略冷静一下,让模型再训练一段时间,再重启监测模式。
-
min_lr(float or list)- 学习率下限,可为 float,或者 list,当有多个参数组时,可用 list 进行设置。
-
eps(float)- 学习率衰减的最小值,当学习率变化小于 eps 时,则不调整学习率。
optimizer = torch.optim.SGD(model.parameters(), args.lr,
momentum=args.momentum ,
weight_decay=args.weight_decay)
scheduler = ReducelROnPlateau(optimizer,'min')
for epoch in range( args.start epoch, args.epochs ):
train(train_loader , model, criterion, optimizer, epoch )
result_avg, loss_val = validate(val_loader, model, criterion, epoch)
# Note that step should be called after validate()
scheduler.step(loss_val )
6 自定义调整学习率 LambdaLR
为不同参数组设定不同学习率调整策略。调整规则为,
$lr=base_lr∗lmbda(self.last_epoch) $
fine-tune 中十分有用,我们不仅可为不同的层设定不同的学习率,还可以为其设定不同的学习率调整策略。
torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda, last_epoch=-1)
参数:
-
lr_lambda(function or list)- 一个计算学习率调整倍数的函数,输入通常为 step,当有多个参数组时,设为 list.
-
last_epoch (int) – 上一个 epoch 数,这个变量用来指示学习率是否需要调整。当
last_epoch 符合设定的间隔时,就会对学习率进行调整。当为-1 时,学习率设置为初始
值。
ignored_params = list(map(id, net.fc3.parameters()))
base_params = filter(lambda p: id(p) not in ignored_params, net.parameters())
optimizer = optim.SGD([
{'params': base_params},
{'params': net.fc3.parameters(), 'lr': 0.001*100}], 0.001, momentum=0.9,weight_decay=1e-4)
# Assuming optimizer has two groups.
lambda1 = lambda epoch: epoch // 3
lambda2 = lambda epoch: 0.95 ** epoch
scheduler = LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])
for epoch in range(100):
train(...)
validate(...)
scheduler.step()
print('epoch: ', i, 'lr: ', scheduler.get_lr())
输出:
epoch: 0 lr: [0.0, 0.1]
epoch: 1 lr: [0.0, 0.095]
epoch: 2 lr: [0.0, 0.09025]
epoch: 3 lr: [0.001, 0.0857375]
epoch: 4 lr: [0.001, 0.081450625]
epoch: 5 lr: [0.001, 0.07737809374999999]
epoch: 6 lr: [0.002, 0.07350918906249998]
epoch: 7 lr: [0.002, 0.06983372960937498]
epoch: 8 lr: [0.002, 0.06634204312890622]
epoch: 9 lr: [0.003, 0.0630249409724609]
为什么第一个参数组的学习率会是 0 呢? 来看看学习率是如何计算的。
第一个参数组的初始学习率设置为 0.001,
lambda1 = lambda epoch: epoch // 3,
第 1 个 epoch 时,由 lr = base_lr * lmbda(self.last_epoch),
可知道 lr = 0.001 *(0//3) ,又因为 1//3 等于 0,所以导致学习率为 0。
第二个参数组的学习率变化,就很容易看啦,初始为 0.1, lr = 0.1 * 0.95^epoch ,当
epoch 为 0 时, lr=0.1 , epoch 为 1 时, lr=0.1*0.95。
7 CyclicLR
torch.optim.lr_scheduler.CyclicLR(optimizer, base_lr, max_lr, step_size_up=2000, step_size_down=None, mode='triangular', gamma=1.0, scale_fn=None, scale_mode='cycle', cycle_momentum=True, base_momentum=0.8, max_momentum=0.9, last_epoch=-1)
step源码
在 PyTorch 中,学习率的更新是通过 scheduler.step(),而我们知道影响学习率的一个重要参数就是 epoch,而 epoch 与 scheduler.step()是如何关联的呢?这就需要看源码了。
def step(self, epoch=None):
if epoch is None:
epoch = self.last_epoch + 1
self.last_epoch = epoch
for param_group, lr in zip(self.optimizer.param_groups, self.get_lr()):
param_group['lr'] = lr
函数接收变量 epoch,默认为 None,当为 None 时, epoch = self.last_epoch + 1。从这里知道, last_epoch 是用以记录 epoch 的。上面有提到 last_epoch 的初始值是-1,因此,第一个 epoch 的值为 -1+1 =0。接着最重要的一步就是获取学习率,并更新。
由于 PyTorch 是基于参数组的管理方式,这里需要采用 for 循环对每一个参数组的学习率进行获取及更新。这里需要注意的是 get_lr(), get_lr()的功能就是获取当前epoch,该参数组的学习率。
这里以 StepLR()为例,介绍 get_lr(),请看代码:
def get_lr(self):
return [base_lr * self.gamma ** (self.last_epoch // self.step_size) for
base_lr in self.base_lrs]
由于 PyTorch 是基于参数组的管理方式,可能会有多个参数组,因此用 for 循环,返
回的是一个 list。 list 元素的计算方式为
base_lr * self.gamma ** (self.last_epoch // self.step_size)。
在执行一次 scheduler.step()之后, epoch 会加 1,因此scheduler.step()要放在 epoch 的 for 循环当中执行。
学习率下降例子
import torch
from torch.optim import lr_scheduler
class TwoLayerNet(torch.nn.Module):
def __init__(self, D_in, H, D_out):
"""
In the constructor we instantiate two nn.Linear modules and assign them as
member variables.
"""
super(TwoLayerNet, self).__init__()
self.linear1 = torch.nn.Linear(D_in, H)
self.linear2 = torch.nn.Linear(H, D_out)
def forward(self, x):
"""
In the forward function we accept a Tensor of input data and we must return
a Tensor of output data. We can use Modules defined in the constructor as
well as arbitrary operators on Tensors.
"""
h_relu = self.linear1(x).clamp(min=0)
y_pred = self.linear2(h_relu)
return y_pred
N, D_in, H, D_out = 64, 1000, 100, 10
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)
# Construct our model by instantiating the class defined above
model = TwoLayerNet(D_in, H, D_out)
criterion = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
print('learning rate: {}'.format(optimizer.param_groups[0]['lr']))
print('weight decay: {}'.format(optimizer.param_groups[0]['weight_decay']))
# scheduler = lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)
# scheduler = lr_scheduler.MultiStepLR(optimizer, [50, 100], 0.5)
gamma = 0.9
scheduler = lr_scheduler.ExponentialLR(optimizer, gamma=gamma)
for t in range(200):
# Forward pass: Compute predicted y by passing x to the model
y_pred = model(x)
# Compute and print loss
scheduler.step()
loss = criterion(y_pred, y)
if t %25 ==0:
print(t, loss.item())
print('t:',t, scheduler.get_lr()[0])
print('learning rate: {}'.format(optimizer.param_groups[0]['lr']))
print(1e-3*gamma**t)
# print('weight decay: {}'.format(optimizer.param_groups[0]['weight_decay']))
# Zero gradients, perform a backward pass, and update the weights.
optimizer.zero_grad()
loss.backward()
optimizer.step()
# scheduler.step() 在一次循环中只能出现一次
手动改学习率
# 一个参数组
#optimizer.param_groups 返回是一个list
#optimizer.param_groups[0]返回的是字典
optimizer.param_groups[0]['lr'] = 1e-5
# 多个参数组
def set_learning_rate(optimizer, lr):
for param_group in optimizer.param_groups:
param_group['lr'] = lr