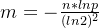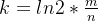目录
一. 情景导入
假设有这么一种情景:
你是一家负责做浏览器的公司,对于某些不健康的网址,你希望你能够在用户访问这些网址时,弹出提示,提醒用户此网站为风险网站,这些所需要添加的网站即为黑名单。如果说,你有一份黑名单,其中黑名单中有100亿条url,即网址,同时每个url的内存为64byte,如果我们正常将其全部存储下来,需要耗费640G的内存,这种开销是及其不合理的,那么我们该如何进行改进呢?
二. bit数组
2.1 数组介绍
(在Java中),一个int类型数组,我们假设其大小为100,则该数组所占用的内存空间为400byte
同理,一个long类型的数组,假设其大小也为100,则该数组所占用内存空间为800byte
我们知道, 1byte=8bit
如果是一个bit类型的数组,在其大小也为100的情况,其所占的内存空间大小仅为 100bit,即12.5byte
由此可见,当使用bit数组来进行存储的时候,所消耗的内存空间是比较小的,那么,我们该如何实现bit数组的结构呢?
2.2 数组构建
以下,我将介绍一下bit数组的使用以及构建,代码整体如下:
package com.atguigu.algorithm;
public class BitMap {
public static void main(String[] args) {
int[] arr=new int[10]; //32bit * 10 ->320bits
//arr[0] int 0~31
//arr[1] int 32~63
//arr[2] int 64~95
int i=178; //想取得第178个bit的状态
int numIndex=178/32;
int bitIndex=178%32;
//拿到178位的状态
int s=(arr[numIndex]>>(bitIndex))&1;
//把第178位的状态改为1
arr[numIndex]=arr[numIndex]|(1<<(bitIndex));
//把第178位的状态改为0
arr[numIndex]=arr[numIndex]&(~(1<<(bitIndex)));
}
}2.3 bit数组详解
接下来,我会对以上的bit数组的操作进行解释:
首先是拿到第178位的状态,int数组中的每一个数都有32个bit位,所以我们得先知道第178位在哪个数上,即 numIndex=178/32,而在当前数上的32个bit位中,第178位在哪个bit位上,即 bitIndex=178%32
当我们想要拿到第178位的状态时,我们将arr[numIndex]右移bitIndex 位,此时能将第178位上的数移动到32个bit位的最右边,然后将其与1进行&操作,若得到为1,则说明178位上为1,若得到为0,说明178位上为0.
接下来的操作是将第178位的状态改为1,我们已经知道第178位的位置了,我们使用arr[numIndex]=arr[numIndex]|(1<<(bitIndex)) 操作就可以将178位改为1,即将1左移 bitIndex位,此时1就会跟第178位bit位对齐,此时由于或的关系,1的那位已经是1了,所以第178位也会被改为1
最后的操作是将第178位的状态改为0,与上面改为1的方式类似,我们使用arr[numIndex]=arr[numIndex]&(~(1<<(bitIndex))) 操作就可以将178位改为0,首先1左移bitIndex到相应位置,然后再将1进行取反,然后再跟arr[numIndex] 进行&操作,1取反后,只有178位为0,其他位置都为1,&操作后 能只让178位的状态改为0.
三. 布隆过滤器
3.1 布隆过滤器介绍
我们回到上述的黑名单问题中,接下来我们提出一种解决方式如下:
创建一个大小为m的bit数组,然后将黑名单中的url依次记为 url1,url2....我们设计出 k 个哈希函数,然后将 url1用K个哈希函数计算得到K个哈希值 hash1, 我们再将 hash1 % m 得到K个 大小为0-m-1的值,然后我们将 bit数组中 K个对应位置都描黑(标记为1),以此往复将 url2 ,以及后续url都这样操作并将相应位置涂黑。
随后,当用户输入一个网址时,我们就将用户输入的网址也同样用K个哈希值计算后,如果发现在bit 数组中 这K个 位置都为描黑的位置,则将用户输入的网址判定为黑名单。
由于哈希函数的特性之一为,相同的输入得到的是相同的结果,因此用户输入的为黑名单中的时,我们一定能够判断出用户输入的是黑名单网址
但布隆过滤器也会出现误判的情况,比如说用户输入的是一个白名单中的网址,我们却将它误判为黑名单的网址,这是由于发生哈希碰撞而难以避免的,我们就将误判的情况下称为失误,有一个指标为 失误率 p
3.2 布隆过滤器 的参数详解
3.2.1 对bit数组大小m 的探究
我们发现如果bit 数组的大小m 过小,此时可能会发生的情况是 整个 bit 数组 全是黑的情况下,此时我们输入的所有网址都会被判定为黑名单。 如果bit 数组的大小越大,此时 bit 数组中留白的区域就越大,此时就能保证失误率越小
因此,在保证数据总量n 不变的情况下,我们可以做出 失误率 p 和 bit数组大小m 之间的关系图像
其函数图像大致贴近于反比例函数
3.2.2 对哈希函数个数k 的探究
哈希函数 的个数k 比较小的时候,比如为1的时候,此时虽然能保证失误率p 并不高,但是在一定范围内,增加哈希函数的个数 能够减小 失误率; 如果哈希函数的个数过多,此时就会使得,一个url 却有特别多的描黑,使得 bit 数组中描黑部分大大增加,使得失误率p也大大增加。
我们在保证 bit数组大小 m不变时,可大致做出 哈希函数个数k 与失误率 p 之间的图像
其图像大致如上,其规律与对勾函数相仿,即有一个最合适的k值
四. 布隆过滤器的几个公式
我们记 n 为样本量,p 为失误率, m为 bit数组的大小,则有如下三个公式:
bit数组大小:
哈希函数个数k:
失误率的真实值p:
这些公式也不需要背下来,在需要使用的时候查询一下即可
公式的具体推导过程,有需要可以自己去查看相关论文
五. 总结
布隆过滤器的使用一般需求是 可以增,可以查,但是不能删
布隆过滤器的具体代码,这里也不给出了
布隆过滤器的难点也仅在 bit 数组的实现,以及 k个 哈希函数的设计
具体设计可以根据自己个人的需求来设计布隆过滤器,总体并不算太难
感谢各位的观看,希望你们能够学到一些东西!