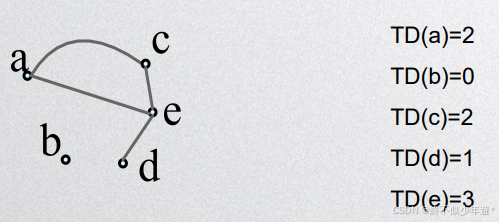图
1. 图的定义和术语
1.1 生活中的图
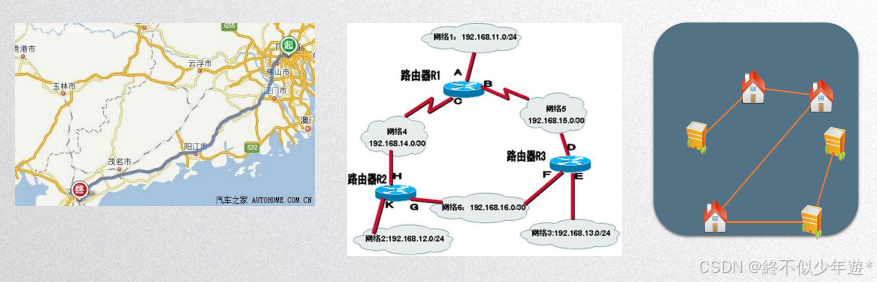
1.2 图的定义和术语
图由点和边连接组成,一些复杂的图中点和边会有相应的权值
1.2.1符号定义:G = (V,E)
节点集合V,其中的元素称为节点或者顶点
边集合E,其中的元素称为边
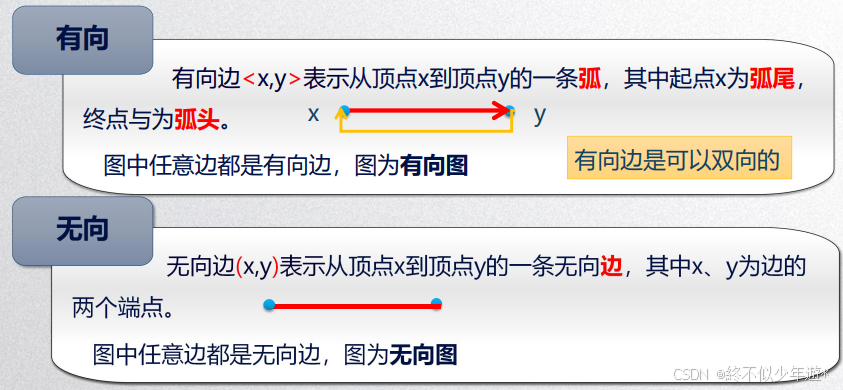
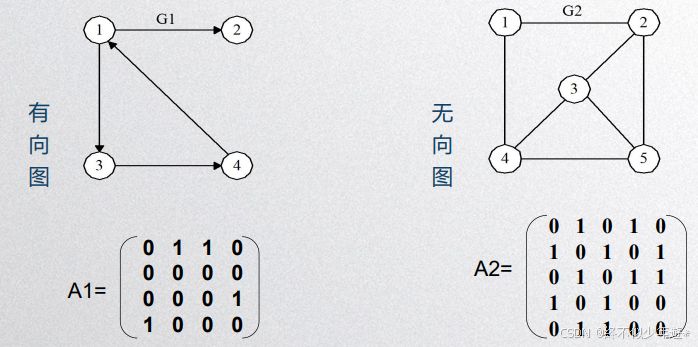
1.2.2 有向图和无向图
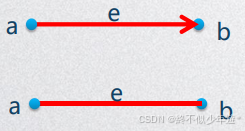
有向图中,一个点到另一个点的边指向性是单一的,例如A->B表示A有一条可以通向B的路,但不代表B也有一条可以通向A的路;无向图则表示AB互通
1.3 完全图、稀疏图和稠密图
1.3.1完全图:
有向完全图:任意两个顶点都有方向相反的有向边
无向完全图:任意两点都有边相连
1.3.2 稀疏图:
假设一幅图有n个节点m条边,当 m<nlog2n,即边的数量远小于节点的数量的图
1.3.3 稠密图:
假设一幅图有n个节点m条边,当 m>nlog2n,即边的数量远大于节点的数量的图
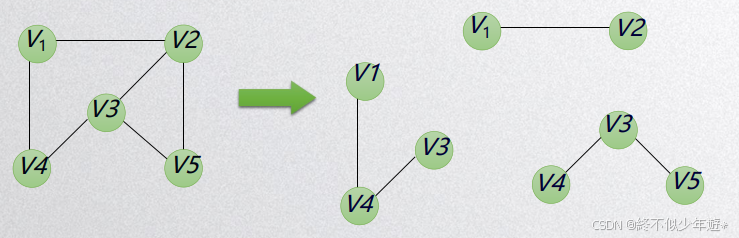
1.4 子图
对于一幅图G = (V,E),若有另一幅图G' = (V',E'),当V包含V'、E包含E'时,G'是G的子图,可以用集合来理解G={1,2,3,4},G'={3,4}
1.5 邻接点
在图(有向图、无向图)中,若节点a和节点b是边e的两个端点,则a和b是邻接的,边e关联与点a和点b
1.6 度、入度和出度
1.6.1 对于无向图,只有度的概念
在无向图中,一个节点的度是指与该节点直接相连的边的数量。这个度量反映了节点的连接强度。
1.6.2 对于有向图则有入度和出度的概念
入度:在有向图中,一个节点的入度是指从其他节点指向该节点的边的数量。这反映了有多少其他节点指向该节点。
出度:相应地,一个节点的出度是指从该节点指向其他节点的边的数量。这反映了该节点对其他节点的控制或影响程度。
图中,OD代表出度、ID代表入度
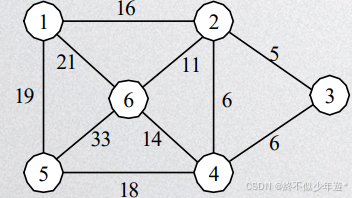
1.7 权值与网
图中两个节点之间的边带上一个有意义的数,称为边的权值,即边权
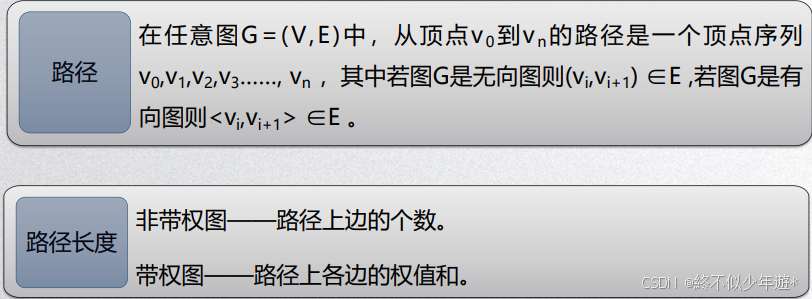
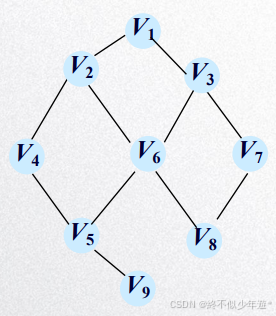
1.8 路径与回路
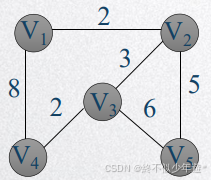
图中V1V4的长度是8;V1V4V3V2V5的长度是两相邻的点之间边权的顺序和8+2+3+5=18
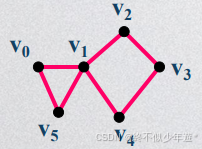
V0V1V2V3V4是一条简单路径
V0V1V5是一条简单回路
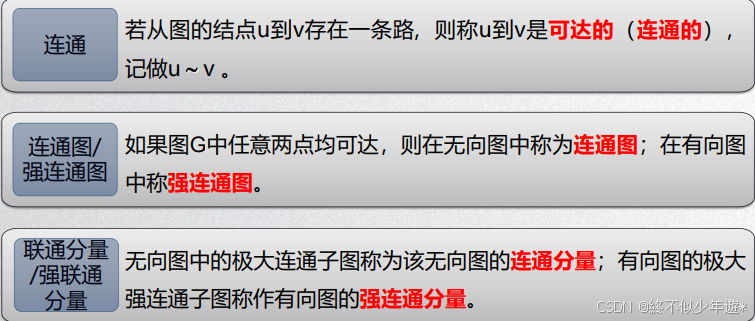
1.9 连通图
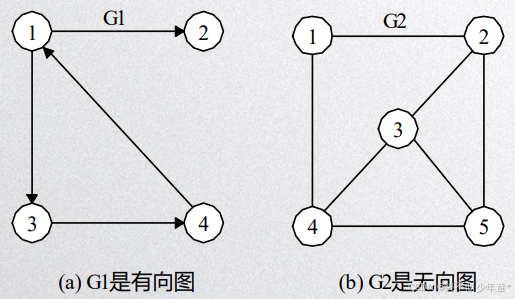
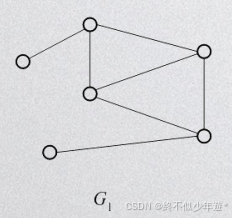
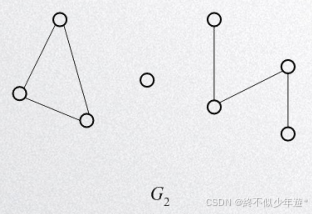
G1是无向图,容易两点均有边连接,即可到达,是连通图
G2中有三个独立的连通块,极大连通子图并不是最大连通子图,G2中有3个连通分量
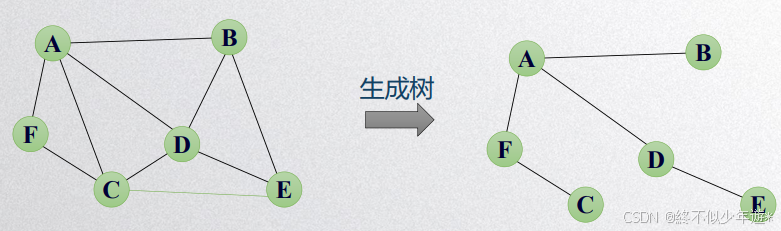
1.10 生成树
生成树指的是连通图中的极小连通子图
每两个点之间都存在一条可达到路径,如果有边权则生成树是原图边权之和最小的子图
2. 图的储存结构
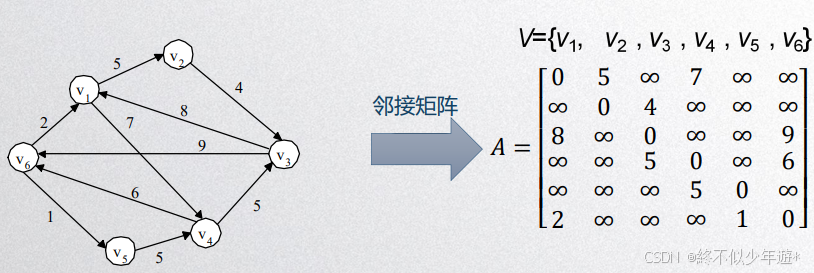
2.1 数组表示法(邻接矩阵)
2.1.1不带权简单图的邻接矩阵
2.1.2带权简单图的邻接矩阵
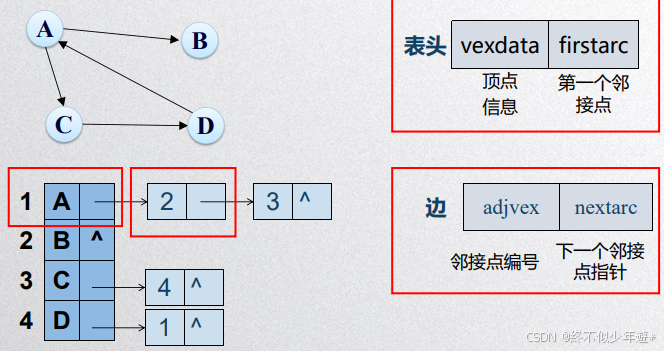
2.2 邻接表
2.2.1不带权邻接表
2.2.2带权邻接表
3. 图的遍历
对于图的遍历,要求是把一个图中的所有节点不重复、不遗漏地访问一次
不重复:图中可能存在环路,访问过的顶点避免重复访问
不遗漏:
按照一定次序进行访问,比如接下来提到的两种方法,深度优先搜索DFS、广度优先搜索BFS
保证不连通图的各个顶点均被访问到(遍历的过程存在回退的情况)
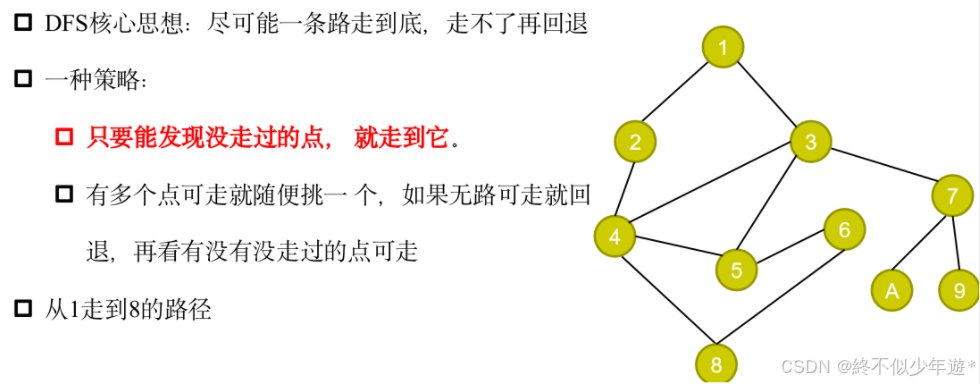
3.1 深度优先搜索DFS
DFS是基于栈的数据结构去实现,尽可能一条路走到底,如果还没完成全图的遍历再回退,然后选择可行路径继续走。
对于这个图,要求使用DFS,从V1出发,优先访问序号小的顶点,访问完全图
遍历过程:V1 V2 V4 V5 V6 V3 V7 V8(V9还没有访问,进行回退。回退到V7 V3 V6 V5此时V5与V9连通) V9
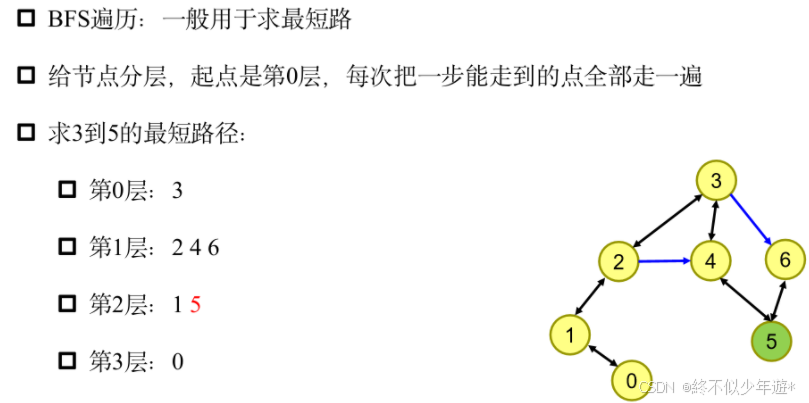
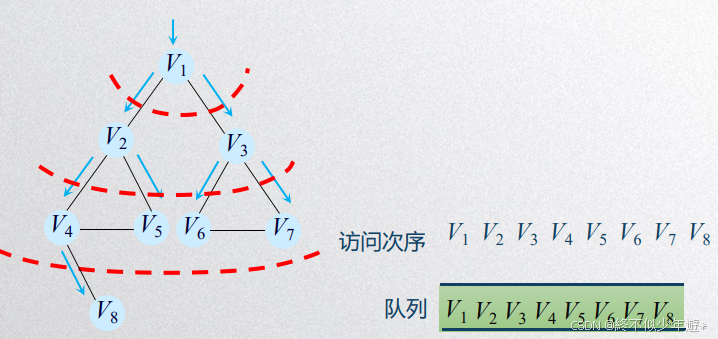
3.2 广度优先搜索 BFS
BFS是基于队列的数据结构实现,在python中通常使用优先队列,遍历时,先把起点加入队列,然后找寻与当前点连通的点中距离最近的继续加入队列,直到跑完全图。
遍历的策略
4. 图的应用
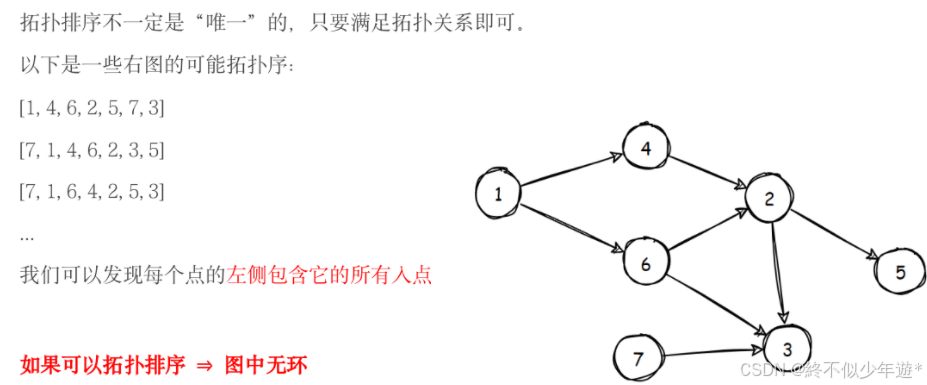
4.1 拓扑排序
拓扑排序针对有向无环图的顶点进行线性排列的算法,使得对于任何来自顶点A指向顶点B的边,A都在序列中出现在B之前。这样的排序存在于有向无环图中,而对于非有向无环图则不存在拓扑排序。
拓扑排序也可以用来检测图中有无成环
4.2 最小生成树
生成树是连通图的极小连通子图,多一条边就会成环,少一条边即无法构成连通图
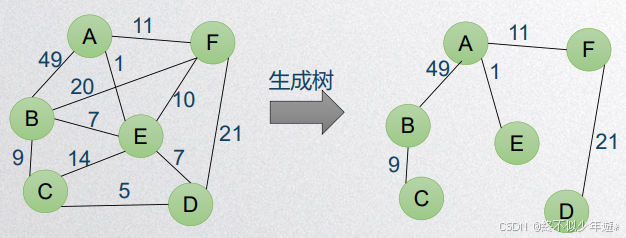
生成树的代价:
G=(V,E)是一个无向连通图,代价是生成树上各边的边权和
生成树代价=9+49+11+1+21=91
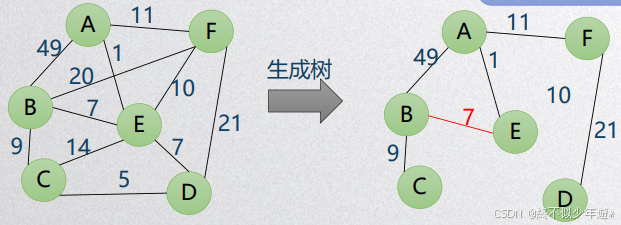
最小生成树即是代价最小的生成树
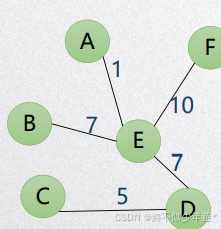
上图中代价min=1+7+10+7+5=30
4.3 最短路问题
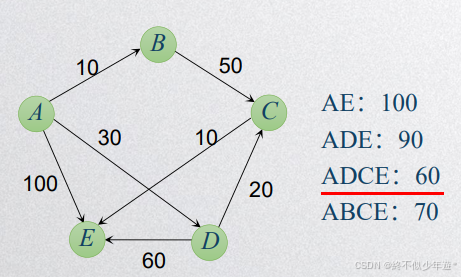
最短路径是两个顶点之间经历的边上边权之和最小的可达路径
4.3.1 Floyed
用于处理多源最短路,从多个点出发到一个点的最短路,可以存在负权边。
4.3.2 Dijkstra
用于处理单源最短路,从一个点出发到一个点的最短路,不可以存在负权边。