学习笔记：在华为云ModelArts上运行MindSpore扩散模型教程

一、背景与目的

二、环境搭建

三、模型原理学习

1. 类定义与初始化

教程来源：MindSpore

一、背景与目的

最近对生成模型非常感兴趣，尤其是扩散模型（Diffusion Models），它在图像生成等领域取得了显著成果。为了深入理解扩散模型的原理和实现，我选择在华为云的ModelArts平台上运行MindSpore官方提供的扩散模型教程。希望通过这次实践，能够掌握扩散模型的基本架构、训练过程以及生成图像的原理。

二、环境搭建

华为云ModelArts平台：注册并登录华为云账号，创建一个ModelArts项目，选择合适的计算资源（如GPU资源）。

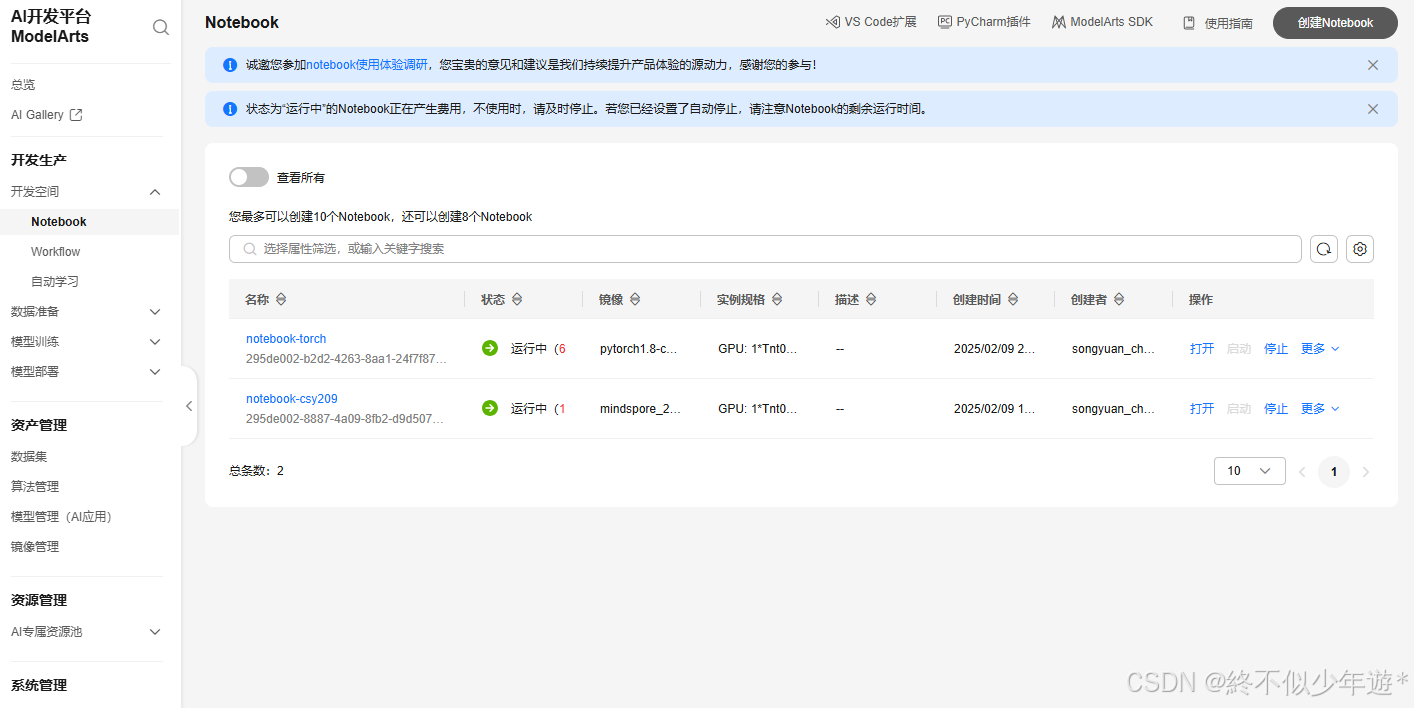
创建一个notebook

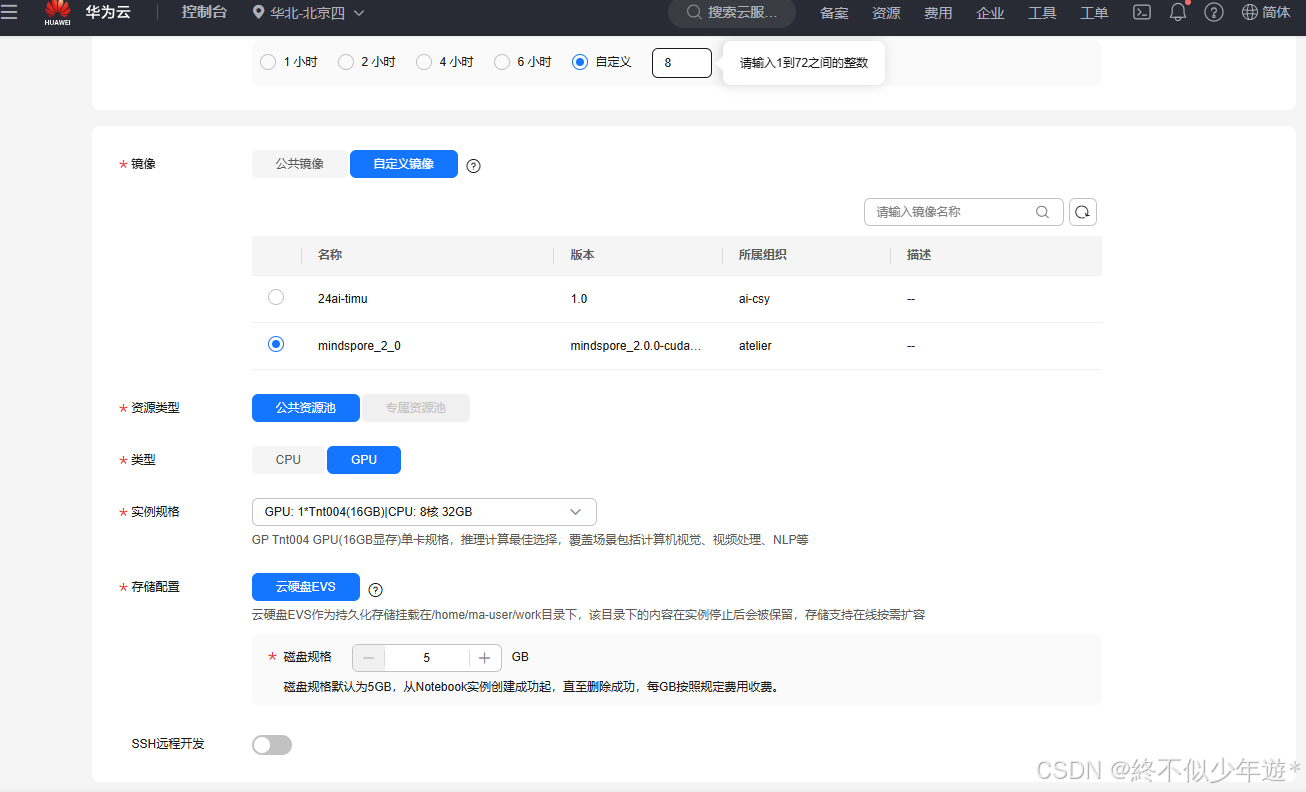
选择好AI框架的镜像，再选择GPU模式，磁盘存储默认即可

MindSpore框架：在ModelArts环境中安装MindSpore框架。可以通过华为云提供的镜像或手动安装MindSpore来完成。

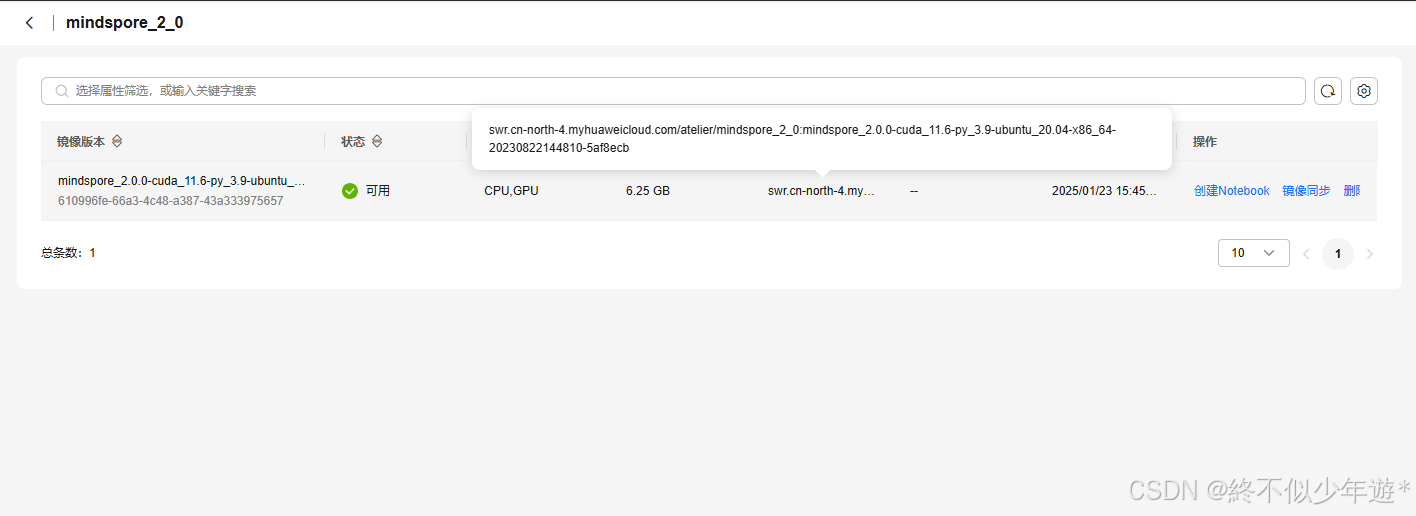
这里我选择在镜像市场拉了一个mindspore2.0版本的镜像

依赖库安装：根据教程要求，安装所需的依赖库，如numpy、matplotlib、tqdm等。在ModelArts的Jupyter Notebook环境中，使用pip install命令进行安装。

三、模型原理学习

扩散模型概述：扩散模型是一种生成模型，通过逐步添加噪声将数据分布转换为简单分布（如高斯分布），然后通过学习逆向去噪过程生成数据样本。它包括正向扩散过程和逆向去噪过程。正向过程是将高斯噪声逐渐添加到图像中，直到变成纯噪声；逆向过程是通过神经网络从纯噪声逐渐去噪，最终生成实际图像。
前向过程与逆向过程：
1. 前向过程：根据预定义的方差计划，在每个时间步长添加高斯噪声。使用公式q(xt ∥xt−1 )=N(xt ;1−βt xt−1 ,βt I)来实现噪声的添加。
2. 逆向过程：利用神经网络学习条件概率分布pθ (xt−1 ∥xt )，通过优化目标函数（如均方误差）来训练神经网络预测噪声，从而实现去噪。
U-Net神经网络：教程中使用U-Net作为神经网络架构，它包含编码器、解码器和瓶颈层，通过残差连接改善梯度流。U-Net能够接收带噪声的图像，并预测添加到输入中的噪声，从而实现逆向去噪。

class Unet(nn.Cell):
    def __init__(
            self,
            dim,
            init_dim=None,
            out_dim=None,
            dim_mults=(1, 2, 4, 8),
            channels=3,
            with_time_emb=True,
            convnext_mult=2,
    ):
        super().__init__()

        self.channels = channels

        init_dim = default(init_dim, dim // 3 * 2)
        self.init_conv = nn.Conv2d(channels, init_dim, 7, padding=3, pad_mode="pad", has_bias=True)

        dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
        in_out = list(zip(dims[:-1], dims[1:]))

        block_klass = partial(ConvNextBlock, mult=convnext_mult)

        if with_time_emb:
            time_dim = dim * 4
            self.time_mlp = nn.SequentialCell(
                SinusoidalPositionEmbeddings(dim),
                nn.Dense(dim, time_dim),
                nn.GELU(),
                nn.Dense(time_dim, time_dim),
            )
        else:
            time_dim = None
            self.time_mlp = None

        self.downs = nn.CellList([])
        self.ups = nn.CellList([])
        num_resolutions = len(in_out)

        for ind, (dim_in, dim_out) in enumerate(in_out):
            is_last = ind >= (num_resolutions - 1)

            self.downs.append(
                nn.CellList(
                    [
                        block_klass(dim_in, dim_out, time_emb_dim=time_dim),
                        block_klass(dim_out, dim_out, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_out, LinearAttention(dim_out))),
                        Downsample(dim_out) if not is_last else nn.Identity(),
                    ]
                )
            )

        mid_dim = dims[-1]
        self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
        self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
        self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)

        for ind, (dim_in, dim_out) in enumerate(reversed(in_out[1:])):
            is_last = ind >= (num_resolutions - 1)

            self.ups.append(
                nn.CellList(
                    [
                        block_klass(dim_out * 2, dim_in, time_emb_dim=time_dim),
                        block_klass(dim_in, dim_in, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_in, LinearAttention(dim_in))),
                        Upsample(dim_in) if not is_last else nn.Identity(),
                    ]
                )
            )

        out_dim = default(out_dim, channels)
        self.final_conv = nn.SequentialCell(
            block_klass(dim, dim), nn.Conv2d(dim, out_dim, 1)
        )

    def construct(self, x, time):
        x = self.init_conv(x)

        t = self.time_mlp(time) if exists(self.time_mlp) else None

        h = []

        for block1, block2, attn, downsample in self.downs:
            x = block1(x, t)
            x = block2(x, t)
            x = attn(x)
            h.append(x)

            x = downsample(x)

        x = self.mid_block1(x, t)
        x = self.mid_attn(x)
        x = self.mid_block2(x, t)

        len_h = len(h) - 1
        for block1, block2, attn, upsample in self.ups:
            x = ops.concat((x, h[len_h]), 1)
            len_h -= 1
            x = block1(x, t)
            x = block2(x, t)
            x = attn(x)

            x = upsample(x)
        return self.final_conv(x)

引用自Diffusion扩散模型 — MindSpore master documentation

解析：

条件 U-Net 神经网络，用于扩散模型中的逆向去噪过程。

1. 类定义与初始化

class Unet(nn.Cell):
    def __init__(
            self,
            dim,
            init_dim=None,
            out_dim=None,
            dim_mults=(1, 2, 4, 8),
            channels=3,
            with_time_emb=True,
            convnext_mult=2,
    ):
        super().__init__()

Unet 类：继承自 MindSpore 的 nn.Cell，表示这是一个神经网络模块。
参数说明：
- dim：基础维度，用于控制网络中卷积层的通道数。
- init_dim：初始卷积层的输出通道数，默认为 dim // 3 * 2。
- out_dim：最终输出的通道数，默认为输入图像的通道数（channels）。
- dim_mults：一个元组，表示每个分辨率级别上的通道数放大倍数。例如 (1, 2, 4, 8) 表示在四个级别上，通道数分别为 dim、2*dim、4*dim、8*dim。
- channels：输入图像的通道数，默认为 3（RGB 图像）。
- with_time_emb：是否使用时间嵌入（time embedding），用于将时间步长信息编码到网络中。
- convnext_mult：ConvNeXT 块中的扩展倍数，默认为 2。

2. 初始卷积层

self.channels = channels

init_dim = default(init_dim, dim // 3 * 2)
self.init_conv = nn.Conv2d(channels, init_dim, 7, padding=3, pad_mode="pad", has_bias=True)

self.channels：保存输入图像的通道数。
init_dim：计算初始卷积层的输出通道数。如果 init_dim 未指定，则默认为 dim // 3 * 2。
self.init_conv：定义一个卷积层，将输入图像的通道数从 channels 转换为 init_dim。卷积核大小为 7×7，填充为 3，以保持图像的空间尺寸。

3. 时间嵌入模块

if with_time_emb:
    time_dim = dim * 4
    self.time_mlp = nn.SequentialCell(
        SinusoidalPositionEmbeddings(dim),
        nn.Dense(dim, time_dim),
        nn.GELU(),
        nn.Dense(time_dim, time_dim),
    )
else:
    time_dim = None
    self.time_mlp = None

with_time_emb：如果为 True，则启用时间嵌入模块。
time_dim：时间嵌入的维度，设置为 dim * 4。
self.time_mlp：定义一个时间嵌入模块，包含以下部分：
- SinusoidalPositionEmbeddings(dim)：使用正弦位置嵌入将时间步长编码为高维向量。
- nn.Dense(dim, time_dim)：将嵌入向量的维度从 dim 扩展到 time_dim。
- nn.GELU()：应用 GELU 激活函数。
- nn.Dense(time_dim, time_dim)：再次将维度扩展到 time_dim。
如果 with_time_emb 为 False，则时间嵌入模块为空。

4. 下采样模块

self.downs = nn.CellList([])
self.ups = nn.CellList([])
num_resolutions = len(in_out)

for ind, (dim_in, dim_out) in enumerate(in_out):
    is_last = ind >= (num_resolutions - 1)

    self.downs.append(
        nn.CellList(
            [
                block_klass(dim_in, dim_out, time_emb_dim=time_dim),
                block_klass(dim_out, dim_out, time_emb_dim=time_dim),
                Residual(PreNorm(dim_out, LinearAttention(dim_out))),
                Downsample(dim_out) if not is_last else nn.Identity(),
            ]
        )
    )

self.downs：一个 CellList，用于存储所有下采样模块。
in_out：一个列表，包含每个分辨率级别上的输入和输出通道数。
循环：对每个分辨率级别，构建一个下采样模块，包含以下部分：
- 两个 ConvNeXT 块：用于特征提取，每个块的输入通道数为 dim_in，输出通道数为 dim_out。
- 一个 LinearAttention 块：用于注意力机制，提升特征的表达能力。
- 一个下采样操作：如果当前级别不是最后一个级别，则使用 Downsample 操作进行下采样；否则，使用 nn.Identity（即不进行下采样）。

5. 中间模块

mid_dim = dims[-1]
self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)

mid_dim：中间模块的通道数，等于最后一个下采样模块的输出通道数。
self.mid_block1 和 self.mid_block2：两个 ConvNeXT 块，用于进一步提取特征。
self.mid_attn：一个注意力模块，用于增强特征的表达能力。

6. 上采样模块

for ind, (dim_in, dim_out) in enumerate(reversed(in_out[1:])):
    is_last = ind >= (num_resolutions - 1)

    self.ups.append(
        nn.CellList(
            [
                block_klass(dim_out * 2, dim_in, time_emb_dim=time_dim),
                block_klass(dim_in, dim_in, time_emb_dim=time_dim),
                Residual(PreNorm(dim_in, LinearAttention(dim_in))),
                Upsample(dim_in) if not is_last else nn.Identity(),
            ]
        )
    )

self.ups：一个 CellList，用于存储所有上采样模块。
reversed(in_out[1:])：从倒数第二个级别开始，逆序遍历分辨率级别。
循环：对每个分辨率级别，构建一个上采样模块，包含以下部分：
- 两个 ConvNeXT 块：用于特征提取，第一个块的输入通道数为 dim_out * 2（因为会拼接来自下采样模块的特征），输出通道数为 dim_in。
- 一个 LinearAttention 块：用于注意力机制。
- 一个上采样操作：如果当前级别不是最后一个级别，则使用 Upsample 操作进行上采样；否则，使用 nn.Identity。

7. 最终卷积层

out_dim = default(out_dim, channels)
self.final_conv = nn.SequentialCell(
    block_klass(dim, dim), nn.Conv2d(dim, out_dim, 1)
)

out_dim：最终输出的通道数，默认为输入图像的通道数。
self.final_conv：定义一个最终卷积层，包含以下部分：
- 一个 ConvNeXT 块：用于最后的特征提取。
- 一个卷积层：将通道数从 dim 转换为 out_dim，卷积核大小为 1×1。

8. 前向传播

def construct(self, x, time):
    x = self.init_conv(x)

    t = self.time_mlp(time) if exists(self.time_mlp) else None

    h = []

    for block1, block2, attn, downsample in self.downs:
        x = block1(x, t)
        x = block2(x, t)
        x = attn(x)
        h.append(x)

        x = downsample(x)

    x = self.mid_block1(x, t)
    x = self.mid_attn(x)
    x = self.mid_block2(x, t)

    len_h = len(h) - 1
    for block1, block2, attn, upsample in self.ups:
        x = ops.concat((x, h[len_h]), 1)
        len_h -= 1
        x = block1(x, t)
        x = block2(x, t)
        x = attn(x)

        x = upsample(x)
    return self.final_conv(x)

输入：
- x：输入图像。
- time：时间步长信息。
前向传播过程：
- 初始卷积：通过 self.init_conv 将输入图像的通道数从 channels 转换为 init_dim。
- 时间嵌入：如果启用时间嵌入模块，则将时间步长信息通过 self.time_mlp 转换为高维向量。
- 下采样：依次通过每个下采样模块，提取特征并逐步降低图像的空间分辨率。将每个下采样模块的输出特征保存到列表 h 中。
- 中间模块：通过中间模块的两个 ConvNeXT 块和注意力模块，进一步提取特征。
- 上采样：逆序通过每个上采样模块，逐步恢复图像的空间分辨率。在每个上采样模块中，将当前特征与之前保存的特征进行拼接，然后通过两个 ConvNeXT 块和注意力模块进行特征提取。
- 最终卷积：通过最终卷积层，将通道数从 dim 转换为 out_dim，得到最终的输出。

9. 关键点总结

U-Net 结构：网络采用 U-Net 结构，包含下采样模块、中间模块和上采样模块。下采样模块逐步降低图像分辨率，提取高层特征；上采样模块逐步恢复图像分辨率，生成最终输出。
时间嵌入：通过正弦位置嵌入将时间步长信息编码到网络中，使网络能够根据不同的时间步长进行去噪。
注意力机制：在下采样和上采样模块中引入注意力机制，增强特征的表达能力。
特征拼接：在上采样过程中，将当前特征与之前保存的特征进行拼接，保留更多的细节信息，有助于生成更高质量的图像。

这个 U-Net 网络是扩散模型中的核心部分，通过学习逆向去噪过程，能够从纯噪声逐步生成实际图像。

四、代码实现与运行

数据准备：使用Fashion-MNIST数据集进行训练。通过mindspore.dataset模块加载数据集，并进行预处理，包括随机水平翻转、标准化等操作，将图像值缩放到[−1,1]范围内。
模型构建：根据教程提供的代码，构建扩散模型的各个模块，包括位置嵌入模块、ResNet/ConvNeXT块、Attention模块、组归一化模块以及条件U-Net网络。特别注意U-Net网络的结构和参数配置，确保其能够正确接收输入并输出预测噪声。
正向扩散过程实现：定义正向扩散过程的函数q_sample，根据时间步长和噪声计划，将噪声添加到输入图像中。通过可视化不同时间步长下的噪声图像，观察噪声逐渐增加的过程。
训练过程：
1. 定义损失函数p_losses，计算真实噪声和预测噪声之间的均方误差，并结合权重进行优化。
2. 使用Adam优化器进行训练，设置动态学习率（如余弦衰减学习率）。在训练过程中，随机采样时间步长和噪声水平，优化神经网络的参数。
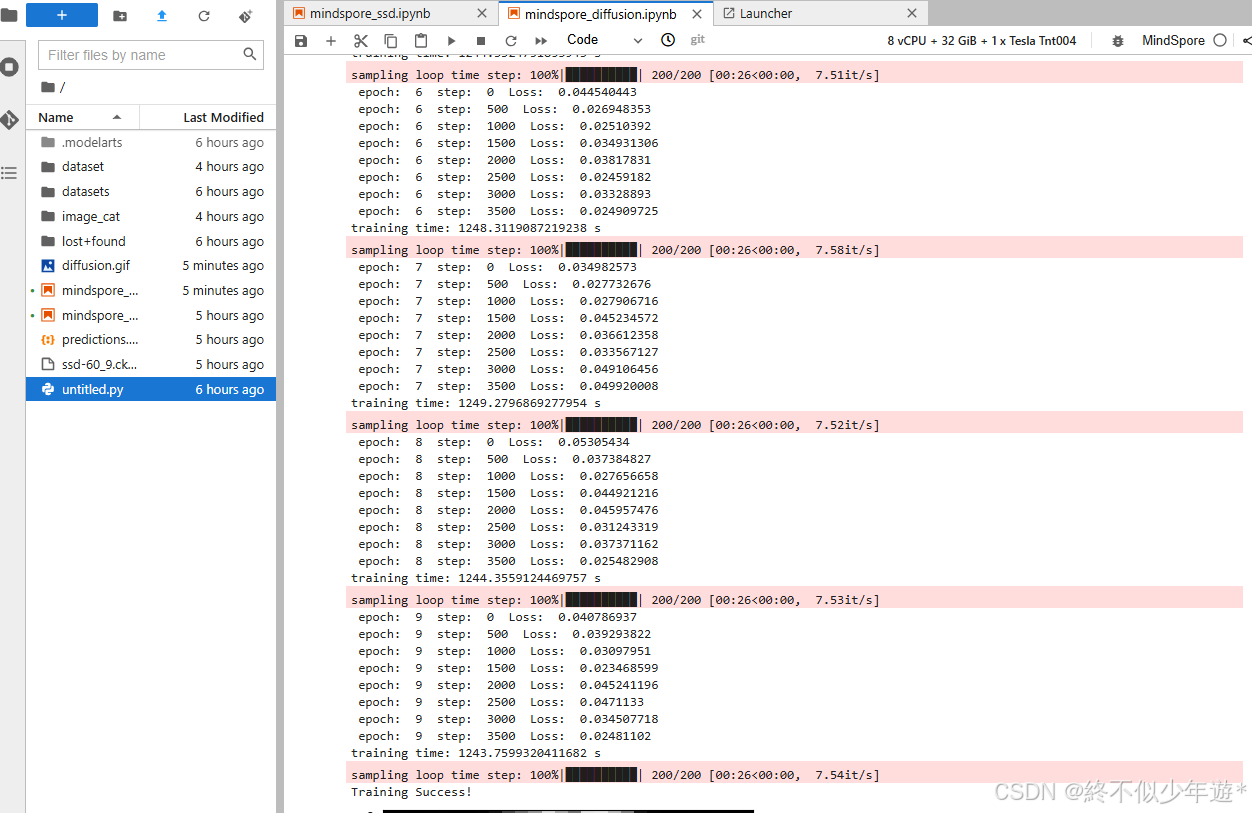
3. 训练过程中，定期打印损失值，观察模型的收敛情况。同时，可以使用采样函数sample在训练过程中生成图像样本，观察模型生成能力的变化。

import time

epochs = 10

iterator = dataset.create_tuple_iterator(num_epochs=epochs)
for epoch in range(epochs):
    begin_time = time.time()
    for step, batch in enumerate(iterator):
        unet_model.set_train()
        batch_size = batch[0].shape[0]
        t = randint(0, timesteps, (batch_size,), dtype=ms.int32)
        noise = randn_like(batch[0])
        loss = train_step(batch[0], t, noise)

        if step % 500 == 0:
            print(" epoch: ", epoch, " step: ", step, " Loss: ", loss)
    end_time = time.time()
    times = end_time - begin_time
    print("training time:", times, "s")
    # 展示随机采样效果
    unet_model.set_train(False)
    samples = sample(unet_model, image_size=image_size, batch_size=64, channels=channels)
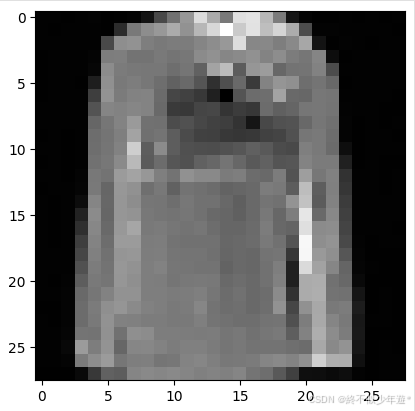
    plt.imshow(samples[-1][5].reshape(image_size, image_size, channels), cmap="gray")
print("Training Success!")

代码来源：Diffusion扩散模型 — MindSpore master documentation

一共训练了10轮

采样与生成：训练完成后，使用采样函数sample从模型中生成图像。通过逐步去噪，从纯噪声生成最终的图像样本。可以展示生成的图像样本，观察模型的生成效果。

生成的效果有些欠佳，可能是随机采样的原因，也可能是模型一些过拟合，需要进一步调整参数

五、遇到的问题及解决方法

环境配置问题：在ModelArts环境中安装MindSpore和依赖库时，可能会遇到版本兼容性问题。解决方法是仔细检查MindSpore和依赖库的版本要求，确保安装的版本相互兼容。可以通过查阅官方文档或社区论坛获取帮助。
训练时间过长：由于扩散模型需要多次正向传递来生成图像，训练过程可能相对较长。解决方法是合理配置计算资源，选择合适的GPU资源加速训练。同时，可以尝试减少训练数据集的大小或调整训练参数（如学习率、批次大小等），以缩短训练时间。
生成效果不佳：在训练过程中，可能会发现生成的图像样本质量不高或存在噪声。解决方法是仔细检查模型的结构和训练参数，确保模型能够正确学习逆向去噪过程。可以尝试调整网络结构、增加训练数据量、优化损失函数等方法来提高生成效果。

六、总结与展望

通过在华为云ModelArts上运行MindSpore扩散模型教程，我对扩散模型的原理和实现有了更深入的理解。扩散模型通过正向扩散和逆向去噪过程，能够生成具有一定质量的图像样本。在实践中，我掌握了MindSpore框架的基本使用方法，以及如何构建和训练扩散模型。同时，我也意识到扩散模型在生成效果和训练效率方面还存在一些挑战，如生成图像的多样性不足、训练时间较长等。

未来，我计划进一步探索扩散模型的改进方法，如引入更复杂的网络结构、优化训练策略等，以提高生成图像的质量和多样性。此外，我还想尝试将扩散模型应用于其他领域，如音频生成、视频生成等，探索其在不同领域的应用潜力。同时，我也会关注扩散模型的最新研究进展，学习和借鉴新的技术和方法，不断提升自己的技术水平。