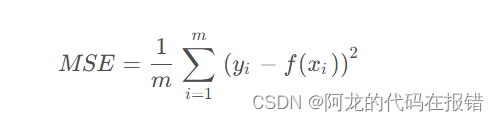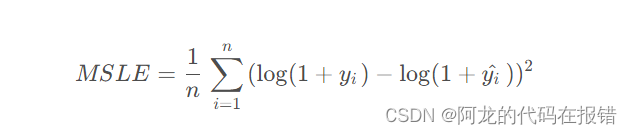数据加载以及数据介绍

import numpy as np
import pandas as pd

data = pd.read_excel('./中国人寿.xlsx')
df = pd.DataFrame(data)
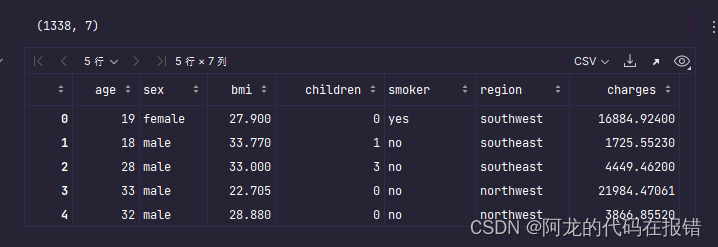
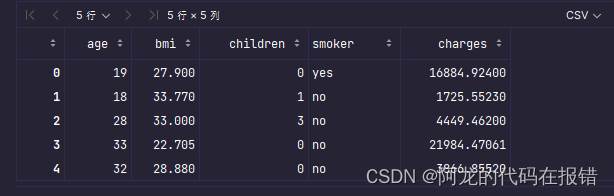
print(data.shape)
data.head()

数据介绍：
* 共计1338条保险数据，每条数据7个属性
* 最后一列charges是保费
* 前面6列是特征，分别为：年龄、性别、体重指数、小孩数量、是否抽烟、所在地区

EDA 数据探索

EDA（Exploratory Data Analysis，数据探索分析）是数据分析的第一步，它旨在了解数据的特征、结构和潜在规律，为进一步分析和建模提供基础。

数据中特征对保费的影响

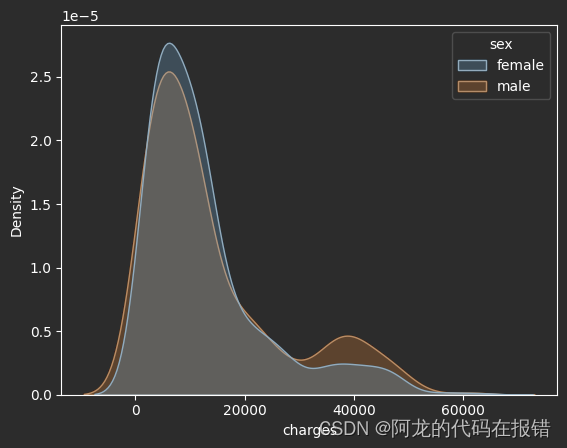
性别对保费影响（从当前的数据呈现的分布来看用于数据分析的意义不大所以进行舍弃）

import seaborn as sns
sns.kdeplot(df,x='charges',fill=True,hue='sex')

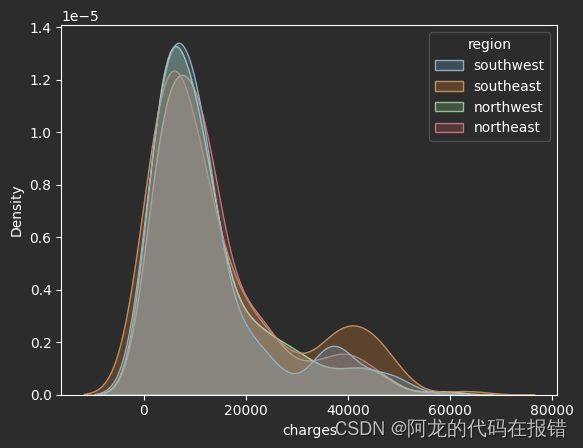
地区对保费的影响（从当前的数据呈现的分布来看用于数据分析的意义不大所以进行舍弃）

sns.kdeplot(df,x='charges',fill=True,hue='region')

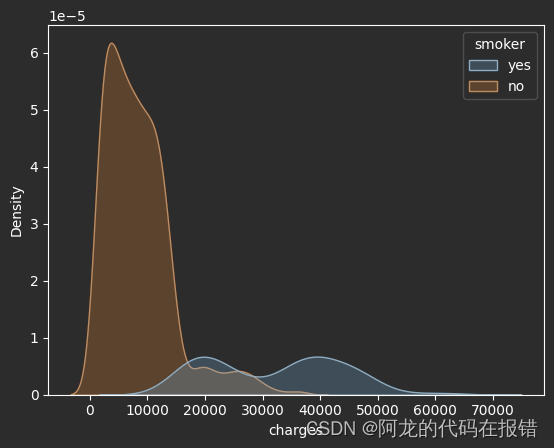
是否抽烟对数据保费的影响

sns.kdeplot(df,x='charges',fill=True,hue='smoker')

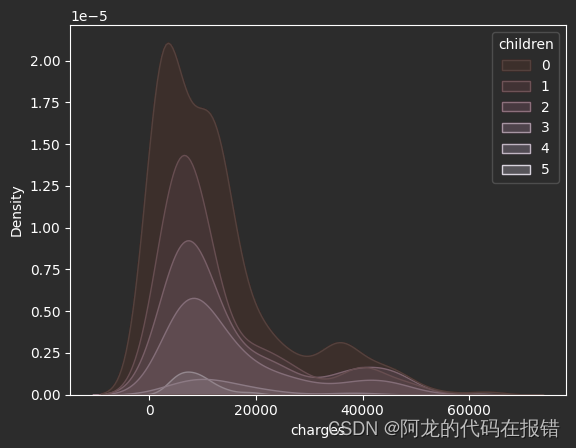
孩子数量对保费的影响

sns.kdeplot(df,x='charges',fill=True,hue='children')

在以上代码中可能出现的问题

出现： ValueError: The following variable cannot be assigned with wide-form data: hue 的问题

import seaborn as sns
# 加载数据
data = pd.read_excel('./XXX.xlsx')
sns.kdeplot(data['charges'], shade=True, hue=data['sex'])

上面的代码写法是老版本的写法了，新版本的写法是需要传入 DataFrame，并指定x轴的数据，新版本写法如下：

# 导包
import pandas as pd

# 将数据转换为DataFrame
data_frame = pd.DataFrame(data)

# 绘制概率分布曲线
sns.kdeplot(data_frame, x='charges', fill=True, hue='sex')

出现这样的问题属于正常的版本迭代的问题，日后出现此类问题建议查看官方文档仔细阅读即可发现解决良药

特征工程

删除不重要特征

data = data.drop(['region', 'sex'], axis=1)
data.head() # 删除不重要特征

# 体重指数，离散化转换，体重两种情况：标准、肥胖
def convert(df,bmi):
    df['bmi'] = 'fat' if df['bmi'] >= bmi else 'standard'
    return df
data = data.apply(convert, axis = 1, args=(30,))
data.head()

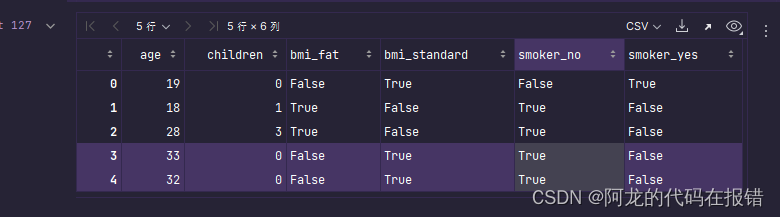
# 特征提取，离散型数据转换为数值型数据
data = pd.get_dummies(data)
data.head()

# 特征和目标值抽取
X = data.drop('charges', axis=1) # 训练数据
y = data['charges'] # 目标值
X.head()

特征升维

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=1024)

# 维度提升
poly = PolynomialFeatures(degree=2,include_bias=False)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.fit_transform(X_test)
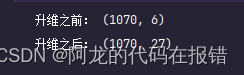
print('升维之前：',X_train.shape)
print('升维之后：',X_train_poly.shape)

模型的训练与评估

引入包

from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNet
# 模型的均方误差
from sklearn.metrics import mean_squared_error, mean_squared_log_error

普通的线性回归

训练模型

# 声明对象
model = LinearRegression()
model.fit(X_train_poly, y_train)
model.score(X_test_poly, y_test)

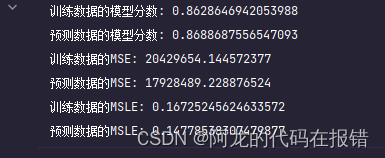
print('训练数据的模型分数:',model.score(X_train_poly, y_train))
print("预测数据的模型分数:", model.score(X_test_poly, y_test))

print('训练数据的MSE:', mean_squared_error(y_train, model.predict(X_train_poly)))
print("预测数据的MSE:", mean_squared_error(y_test, model.predict(X_test_poly)))

print('训练数据的MSLE:', mean_squared_log_error(y_train, model.predict(X_train_poly)))
print("预测数据的MSLE:", mean_squared_log_error(y_test, model.predict(X_test_poly)))

未进行升维的

# 未进行特征升维
model = LinearRegression()
model.fit(X_train, y_train)

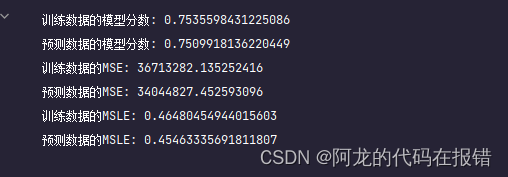
print('训练数据的模型分数:',model.score(X_train, y_train))
print("预测数据的模型分数:", model.score(X_test, y_test))

print('训练数据的MSE:', mean_squared_error(y_train, model.predict(X_train)))
print("预测数据的MSE:", mean_squared_error(y_test, model.predict(X_test)))

print('训练数据的MSLE:', mean_squared_log_error(y_train, model.predict(X_train)))
print("预测数据的MSLE:", mean_squared_log_error(y_test, model.predict(X_test)))

弹性网络回归

# 升维后的数据
model1 = ElasticNet(alpha=0.1,l1_ratio=0.3,max_iter=1000)
model1.fit(X_train_poly,y_train)

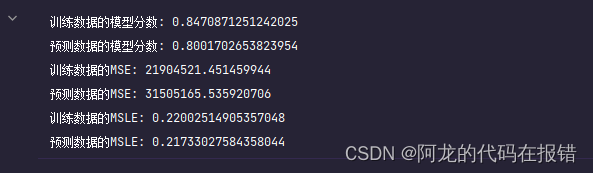
print('训练数据的模型分数:',model1.score(X_train_poly, y_train))
print("预测数据的模型分数:", model1.score(X_test_poly, y_test))

print('训练数据的MSE:', mean_squared_error(y_train, model1.predict(X_train_poly)))
print("预测数据的MSE:", mean_squared_error(y_test, model1.predict(X_test_poly)))

print('训练数据的MSLE:', mean_squared_log_error(y_train, model1.predict(X_train_poly)))
print("预测数据的MSLE:", mean_squared_log_error(y_test, model1.predict(X_test_poly)))

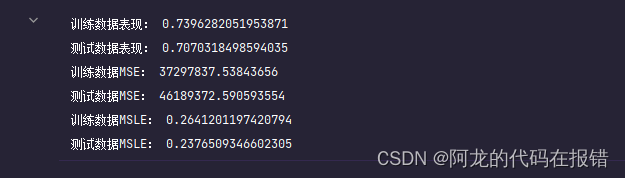
未升维数据对比（表现差强人意，说明升维更棒）

# 未进行特征升维建模预测表现
model = ElasticNet(alpha=0.1,l1_ratio=0.3,max_iter=1000)
model.fit(X_train,y_train)

print('训练数据表现：',model.score(X_train,y_train))
print('测试数据表现：',model.score(X_test,y_test))

print('训练数据MSE：',mean_squared_error(y_train,model.predict(X_train)))
print('测试数据MSE：',mean_squared_error(y_test, model.predict(X_test)))

print('训练数据MSLE：',mean_squared_log_error(y_train,model.predict(X_train)))
print('测试数据MSLE：',mean_squared_log_error(y_test, model.predict(X_test)))

MSE:均方误差（Mean Squared Error，MSE）的缩写，它是指预测值与真实值之间差值的平方的平均值。用数学公式表示为：

MLSE：Mean Squared Logarithmic Error（MSLE）是一种用于衡量回归模型预测误差的指标，它将真实值和预测值取对数后计算MSE。MSLE的值越小，说明模型的预测误差越小。用数学公式表示为：

写在最后：
愿君前程似锦，未来可期去💯,感谢您的阅读，如果对您有用希望您留下宝贵的点赞和收藏
本文章为本人学习笔记，如有请侵权联系，本人会立即删除侵权文章。可以一起学习共同进步谢谢
如有请侵权联系，本人会立即删除侵权文章。