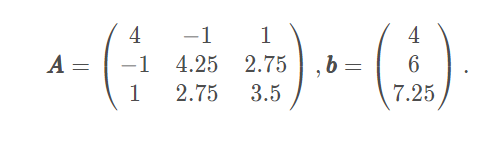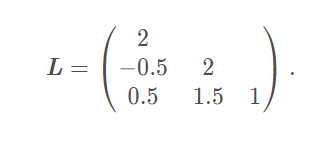本文来源:https://blog.csdn.net/qq_41564404/article/details/88085073
Cholesky分解及一个例子
定义: cholesky分解是一种将任意n阶对称正定矩阵A分解成下三角矩阵L的一种方法:
A
=
L
L
T
A = L L ^ T
A=LLT
其中,L称为Cholesky因子。如果L的对角元均为正数,则L是唯一确定的。
Cholesky分解对于解决带有对称正定系数矩阵A的线性问题非常有效。在计算机中,直接求解
A
x
=
b
Ax=b
Ax=b
时间复杂度是很高的,用cholesky法对A提前变换之后再计算会有效降低复杂度。计算方法如下:
A
x
=
b
⇨
L
L
T
x
=
b
Ax = b⇨LL^Tx=b
Ax=b⇨LLTx=b
等价于
{
L
y
=
b
L
T
x
=
y
\begin{cases} Ly=b\\ L^Tx=y\end{cases}
{Ly=bLTx=y
先因为根据第一行a11得到l11的平方,从而得出l11的值,再由a21可知a21=l21l11,a31=l31l11,……,因由第一部得出l11的值,从而得出li1的值
a
i
1
=
l
11
l
i
1
⇨
l
i
1
=
a
i
1
l
11
(
i
=
2
,
3
,
…
…
,
n
)
ai1 = l11li1 ⇨li1 = \frac{ai1}{l11}(i=2,3,……,n)
ai1=l11li1⇨li1=l11ai1(i=2,3,……,n)
再求lii,因为可以得出a22=l22的平方+l12的平方,已得出l12的值从而可以求得l22的值,以此类推
a
11
=
l
11
2
⇨
l
11
=
a
11
a11 = l~11~^2 ⇨l11 = \sqrt{a11}
a11=l 11 2⇨l11=a11
再因为a32=l31l12+l32l22,……,因前两步得出l31,l12,l22,从而得出l32,以此类推,可得出所有lkk
a
k
k
=
∑
i
=
1
k
l
k
i
2
⇨
l
k
k
=
a
k
k
−
∑
i
=
1
k
−
1
l
k
i
2
~a_kk~=\sum_{i=1}^{k}{lki^2} ⇨ lkk=\sqrt{akk-\sum_{i=1}^{k-1}{lki^2}}
akk =i=1∑klki2⇨lkk=akk−i=1∑k−1lki2
例题
用cholesky方法求解线性方程组Ax=b,其中
显然
A
T
=
A
A^T = A
AT=A
且D1=4>0,D2=16>0,D3=16>0,因此,A为对称正定矩阵,故存在
A
=
L
L
T
A = L L^T
A=LLT
所以
l
11
=
a
11
=
2
,
l
21
=
a
21
l
11
=
−
0.5
,
l
31
=
a
31
l
11
=
0.5
l11 = \sqrt{a11}=2,l21=\frac{a21}{l11}=-0.5,l31 = \frac{a31}{l11}=0.5
l11=a11=2,l21=l11a21=−0.5,l31=l11a31=0.5
l 22 = a 22 − l 1 2 2 = 2 , l 32 = a 32 − l 31 l 21 l 22 = 1.5 , l 33 = 1 l22=\sqrt{a22-l12^2}=2,l32=\frac{a32-l31l21}{l22}=1.5,l33=1 l22=a22−l122=2,l32=l22a32−l31l21=1.5,l33=1
得:
再求:
{
L
y
=
b
L
T
x
=
y
\begin{cases} Ly=b\\ L^Tx=y \end{cases}
{Ly=bLTx=y
解得X=(1,1,1)┬