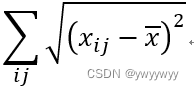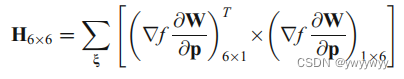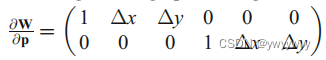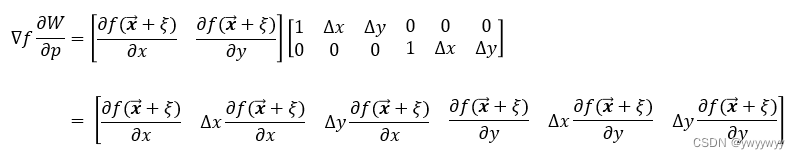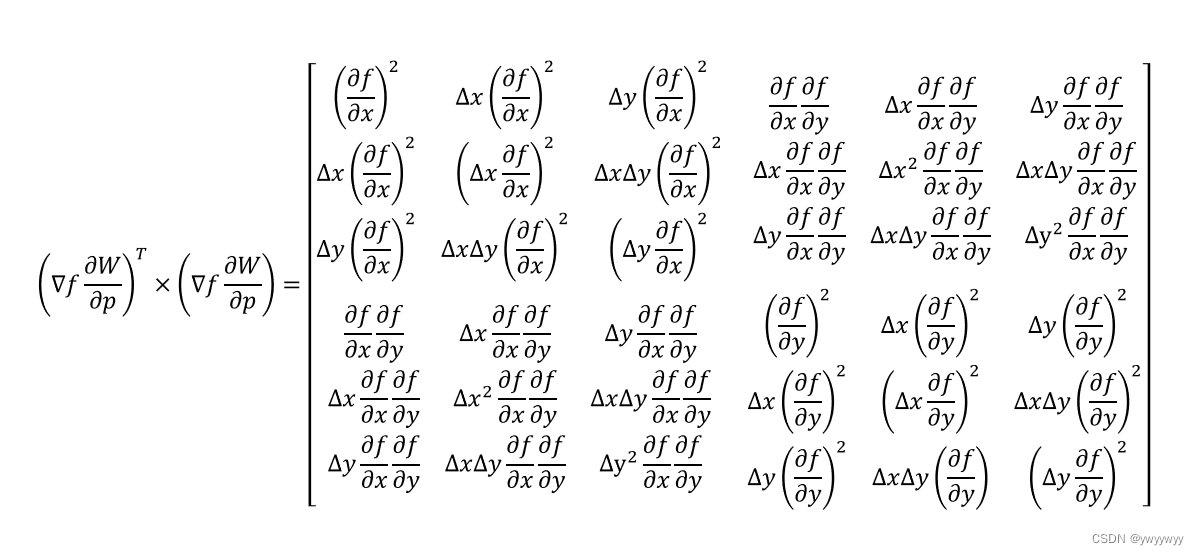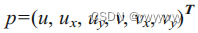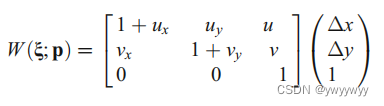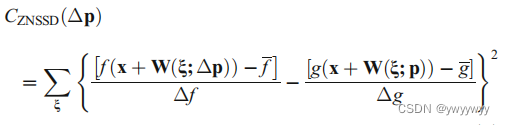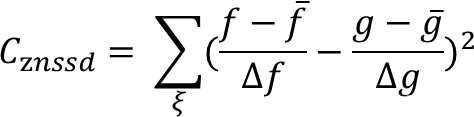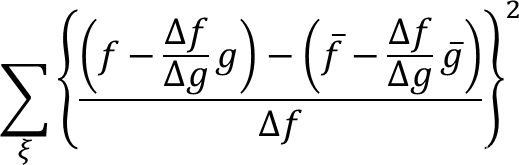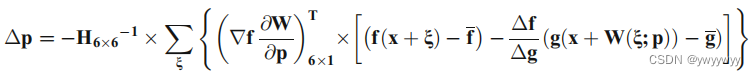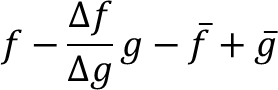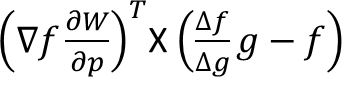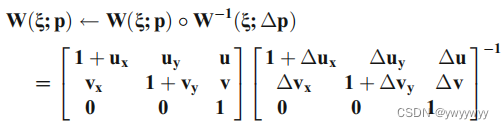Bootstrap

【数字图像相关-Opencorr学习笔记】剖析源码，理解ICGN的具体实现过程

OpenCorr是一个开源C++库，用于研究和开发数字图像相关（DIC）技术它提供了2D和3D-DIC以及数字体积相关（DVC）的功能模块。最近正在学习OpenCorr，为了更深层次地理解ICGN，我打算浅浅剖析Opencorr的代码，学习的过程中写下这篇学习笔记，以后忘记了还能回来看看。同时，作为一名在读研究生，希望能得到社区大佬的指点，以及跟同学们一起学习进步。

OpenCorr的github地址

https://github.com/vincentjzy/OpenCorr

想要学习交流的同学，在看这篇学习笔记之前，首先要看潘兵老师的论文

Fast, Robust and Accurate Digital Image Correlation Calculation Without Redundant Computations

然后我推荐大家最好再看这个博主对ICGN的理论推导，解释的非常通透。

https://blog.csdn.net/weixin_43560489/article/details/121708456?spm=1001.2014.3001.5506

文章目录

一、源码和输入变量

在Opencorr中，简单四行就封装了整个icgn的复杂计算过程，其代码如下：

	ICGN2D1* icgn1 = new ICGN2D1(subset_radius_x, subset_radius_y, max_deformation_norm, max_iteration, cpu_thread_number);
	icgn1->setImages(ref_img, tar_img);
	icgn1->prepare();
	icgn1->compute(poi_queue);

其中subset_radius_x， subset_radius_y是人为设定的窗口半径
max_deformation_norm是最小的迭代距离，即Δp的模
max_iteration是最大的迭代步数，
小于最小距离或者最大步数就会终止程序输出结果。
介绍完输出参数，来看ICGN2D1 new了什么东西，其源码如下：

ICGN2D1::ICGN2D1(int subset_radius_x, int subset_radius_y, float conv_criterion, float stop_condition, int thread_number)
		: ref_gradient(nullptr), tar_interp(nullptr)
	{
		this->subset_radius_x = subset_radius_x;
		this->subset_radius_y = subset_radius_y;
		this->conv_criterion = conv_criterion;
		this->stop_condition = stop_condition;
		this->thread_number = thread_number;

		for (int i = 0; i < thread_number; i++)
		{
			ICGN2D1_* instance = ICGN2D1_::allocate(subset_radius_x, subset_radius_y);
			instance_pool.push_back(instance);
		}
	}

可以看到就是初始化了一些参数，然后根据线程数量进行实例化。
由于allocate里面东西太多就不展开说了。

icgn1->setImages(ref_img, tar_img);这句就是导入原图。

二、prepare()

prepare源码如下：

void ICGN2D1::prepare()
	{
		prepareRef();
		prepareTar();
	}

prepareRef和prepareTar()虽然名字相近，但是要注意，这两个函数干了完全不同的事情。
首先是prepareRef():

void ICGN2D1::prepareRef()
	{
		if (ref_gradient != nullptr)
		{
			delete ref_gradient;
			ref_gradient = nullptr;
		}

		ref_gradient = new Gradient2D4(*ref_img);
		ref_gradient->getGradientX();
		ref_gradient->getGradientY();
	}

其功能是计算x和y方向的一阶导。再深入getGradientX和getGradientY中，看看Opencorr中是怎么计算梯度的。

void Gradient2D4::getGradientX()
	{
		int height = grad_img->height;
		int width = grad_img->width;

		gradient_x = Eigen::MatrixXf::Zero(height, width);

#pragma omp parallel for
		for (int r = 0; r < height; r++)
		{
			for (int c = 2; c < width - 2; c++)
			{
				float result = 0.0f;
				result -= grad_img->eg_mat(r, c + 2) / 12.f;
				result += grad_img->eg_mat(r, c + 1) * (2.f / 3.f);
				result -= grad_img->eg_mat(r, c - 1) * (2.f / 3.f);
				result += grad_img->eg_mat(r, c - 2) / 12.f;
				gradient_x(r, c) = result;	
			}
		}
	}

主要是看嵌套循环中干了什么事情。其实就是用一个一维梯度算子 1/12 * [-1, 8, 0, -8, 1]来计算X方向的梯度。笔者试验了其效果如下：
在这里插入图片描述 在这里插入图片描述
　　　　　　　　(a)原图 　　　　　　　　　　　　　　　　　　　(b)x方向梯度
而getGadientY()是一样的，只是方向不同。
接下来轮到prepareTar()，其代码如下：

void ICGN2D1::prepareTar()
	{
		if (tar_interp != nullptr)
		{
			delete tar_interp;
			tar_interp = nullptr;
		}

		tar_interp = new BicubicBspline(*tar_img);
		tar_interp->prepare();
	}

tar_interp->prepare()计算出全图中每个像素点的双三次B样条插值的4*4系数矩阵。
至此准备工作就完成了，可以开始计算。

三、compute()

以下是compute的整体代码，原版是全英文注解，其中有一些我看代码时候的注解，可以忽略。后面我将逐一拆解其中的代码片段，剖析ICGN的计算过程。

void ICGN2D1::compute(POI2D* poi)
	{
		//set instance w.r.t. thread id 
		ICGN2D1_* cur_instance = getInstance(omp_get_thread_num());

		if (poi->y - subset_radius_y < 0 || poi->x - subset_radius_x < 0
			|| poi->y + subset_radius_y > ref_img->height - 1 || poi->x + subset_radius_x > ref_img->width - 1
			|| fabs(poi->deformation.u) >= ref_img->width || fabs(poi->deformation.v) >= ref_img->height
			|| poi->result.zncc < 0 || std::isnan(poi->deformation.u) || std::isnan(poi->deformation.v))
		{
			poi->result.zncc = poi->result.zncc < -1 ? poi->result.zncc : -1;
		}
		else
		{
			int subset_width = 2 * subset_radius_x + 1;
			int subset_height = 2 * subset_radius_y + 1;

			//set reference subset
			cur_instance->ref_subset->center = (Point2D)*poi;
			cur_instance->ref_subset->fill(ref_img);
			float ref_mean_norm = cur_instance->ref_subset->zeroMeanNorm();//返回 ∑^i_j √((x_ij - x_mean)^2) 即，ref_subset中所有元素减去平均数的平方并且开根号，最后全部加起来

			//build the Hessian matrix
			cur_instance->hessian.setZero();
			for (int r = 0; r < subset_height; r++)
			{
				for (int c = 0; c < subset_width; c++)
				{
					int x_local = c - subset_radius_x;
					int y_local = r - subset_radius_y;
					int x_global = (int)poi->x + x_local;
					int y_global = (int)poi->y + y_local;
					float ref_gradient_x = ref_gradient->gradient_x(y_global, x_global);
					float ref_gradient_y = ref_gradient->gradient_y(y_global, x_global);

					cur_instance->sd_img[r][c][0] = ref_gradient_x;
					cur_instance->sd_img[r][c][1] = ref_gradient_x * x_local;
					cur_instance->sd_img[r][c][2] = ref_gradient_x * y_local;
					cur_instance->sd_img[r][c][3] = ref_gradient_y;
					cur_instance->sd_img[r][c][4] = ref_gradient_y * x_local;
					cur_instance->sd_img[r][c][5] = ref_gradient_y * y_local;

					for (int i = 0; i < 6; i++)
					{
						for (int j = 0; j < 6; j++)
						{
							cur_instance->hessian(i, j) += (cur_instance->sd_img[r][c][i] * cur_instance->sd_img[r][c][j]);
						}
					}
				}
			}

			//calculate the inversed Hessian matrix
			cur_instance->inv_hessian = cur_instance->hessian.inverse();

			//set target subset
			cur_instance->tar_subset->center = (Point2D)*poi;

			//get initial guess
			Deformation2D1 p_initial(poi->deformation.u, poi->deformation.ux, poi->deformation.uy,
				poi->deformation.v, poi->deformation.vx, poi->deformation.vy);

			//IC-GN iteration
			int iteration_counter = 0; //initialize iteration counter
			Deformation2D1 p_current, p_increment;
			p_current.setDeformation(p_initial);
			float dp_norm_max, znssd;
			Point2D local_coor, warped_coor, global_coor;
			do
			{
				iteration_counter++;
				//reconstruct target subset
				for (int r = 0; r < subset_height; r++)
				{
					for (int c = 0; c < subset_width; c++)
					{
						int x_local = c - subset_radius_x;
						int y_local = r - subset_radius_y;
						local_coor.x = x_local;
						local_coor.y = y_local;
						warped_coor = p_current.warp(local_coor);
						global_coor = cur_instance->tar_subset->center + warped_coor;
						cur_instance->tar_subset->eg_mat(r, c) = tar_interp->compute(global_coor);
					}
				}
				float tar_mean_norm = cur_instance->tar_subset->zeroMeanNorm();

				//calculate error image
				cur_instance->error_img = cur_instance->tar_subset->eg_mat * (ref_mean_norm / tar_mean_norm)
					- (cur_instance->ref_subset->eg_mat);

				//calculate ZNSSD
				znssd = cur_instance->error_img.squaredNorm() / (ref_mean_norm * ref_mean_norm);

				//calculate numerator
				float numerator[6] = { 0.f };
				for (int r = 0; r < subset_height; r++)
				{
					for (int c = 0; c < subset_width; c++)
					{
						for (int i = 0; i < 6; i++)
						{
							numerator[i] += (cur_instance->sd_img[r][c][i] * cur_instance->error_img(r, c));
						}
					}
				}

				//calculate dp
				float dp[6] = { 0.f };
				for (int i = 0; i < 6; i++)
				{
					for (int j = 0; j < 6; j++)
					{
						dp[i] += (cur_instance->inv_hessian(i, j) * numerator[j]);
					}
				}
				p_increment.setDeformation(dp);

				//update warp
				p_current.warp_matrix = p_current.warp_matrix * p_increment.warp_matrix.inverse();

				//update p
				p_current.setDeformation();

				//check convergence
				int subset_radius_x2 = subset_radius_x * subset_radius_x;
				int subset_radius_y2 = subset_radius_y * subset_radius_y;

				dp_norm_max = 0.f;
				dp_norm_max += p_increment.u * p_increment.u;
				dp_norm_max += p_increment.ux * p_increment.ux * subset_radius_x2;
				dp_norm_max += p_increment.uy * p_increment.uy * subset_radius_y2;
				dp_norm_max += p_increment.v * p_increment.v;
				dp_norm_max += p_increment.vx * p_increment.vx * subset_radius_x2;
				dp_norm_max += p_increment.vy * p_increment.vy * subset_radius_y2;

				dp_norm_max = sqrt(dp_norm_max);
			} while (iteration_counter < stop_condition && dp_norm_max >= conv_criterion);

			//store the final result
			poi->deformation.u = p_current.u;
			poi->deformation.ux = p_current.ux;
			poi->deformation.uy = p_current.uy;
			poi->deformation.v = p_current.v;
			poi->deformation.vx = p_current.vx;
			poi->deformation.vy = p_current.vy;

			//save the parameters for output
			poi->result.u0 = p_initial.u;
			poi->result.v0 = p_initial.v;
			poi->result.zncc = 0.5f * (2 - znssd);
			poi->result.iteration = (float)iteration_counter;
			poi->result.convergence = dp_norm_max;
		}

		//check if the case of NaN occurs for ZNCC or displacments
		if (std::isnan(poi->result.zncc) || std::isnan(poi->deformation.u) || std::isnan(poi->deformation.v))
		{
			poi->deformation.u = poi->result.u0;
			poi->deformation.v = poi->result.v0;
			poi->result.zncc = -5;
		}
	}

（1）首先看输入值，poi

其类型为POI2D，定义如下：

class POI2D : public Point2D
	{
	public:
		DeformationVector2D deformation;
		Result2D result;
		StrainVector2D strain;
		Point2D subset_radius;

		POI2D(int x, int y);
		POI2D(float x, float y);
		POI2D(Point2D location);
		~POI2D();

		//reset data except the location
		void clear();
	};

其中，DeformationVector2D保存了x，y方向的位移及其各个方向的导数。

union DeformationVector2D
	{
		struct
		{
			float u, ux, uy, uxx, uxy, uyy;
			float v, vx, vy, vxx, vxy, vyy;
		};
		float p[12]; //order: u ux uy uxx uxy uyy v vx vy vxx vxy vyy
	};

Result2D保存了计算的结果

union Result2D
	{
		struct
		{
			float u0, v0, zncc, iteration, convergence, feature;
		};
		float r[6];
	};

StrainVector2D 应变

union StrainVector2D
	{
		struct
		{
			float exx, eyy, exy;
		};
		float e[3]; //order: exx, eyy, exy
	};

最后Point2D主要保存了x和y的坐标

class Point2D
	{
	public:
		float x, y;
		...//此处省略成员函数
	}

（2）设置参考区域

			int subset_width = 2 * subset_radius_x + 1;
			int subset_height = 2 * subset_radius_y + 1;

			//set reference subset
			cur_instance->ref_subset->center = (Point2D)*poi;
			cur_instance->ref_subset->fill(ref_img);
			float ref_mean_norm = cur_instance->ref_subset->zeroMeanNorm();

这一部分初始化了参考区域，首先初始化了区域中心center
fill函数的实现如下，其实就是在原图中截取了subet_width * subset_height大小的block。

void Subset2D::fill(Image2D* image)
	{
		Point2D topleft_point(center.x - radius_x, center.y - radius_y);
		eg_mat << image->eg_mat.block(topleft_point.y, topleft_point.x, height, width);
	}

然后计算了一个zeroMeanNorm，实际就是
在这里插入图片描述
这里还是展示一下源码：

float Subset2D::zeroMeanNorm()
	{
		float subset_mean = eg_mat.mean();//求均值
		eg_mat.array() -= subset_mean;//
		float subset_sum = eg_mat.squaredNorm();

		return sqrt(subset_sum);
	}

（3）构建Hessian矩阵

在讲解代码之前，首先要了解Hessian矩阵，其定义见链接

http://t.csdn.cn/YiqBc

整体代码如下：

			cur_instance->hessian.setZero();
			for (int r = 0; r < subset_height; r++)
			{
				for (int c = 0; c < subset_width; c++)
				{
					int x_local = c - subset_radius_x;
					int y_local = r - subset_radius_y;
					int x_global = (int)poi->x + x_local;
					int y_global = (int)poi->y + y_local;
					float ref_gradient_x = ref_gradient->gradient_x(y_global, x_global);
					float ref_gradient_y = ref_gradient->gradient_y(y_global, x_global);

					cur_instance->sd_img[r][c][0] = ref_gradient_x;
					cur_instance->sd_img[r][c][1] = ref_gradient_x * x_local;
					cur_instance->sd_img[r][c][2] = ref_gradient_x * y_local;
					cur_instance->sd_img[r][c][3] = ref_gradient_y;
					cur_instance->sd_img[r][c][4] = ref_gradient_y * x_local;
					cur_instance->sd_img[r][c][5] = ref_gradient_y * y_local;

					for (int i = 0; i < 6; i++)
					{
						for (int j = 0; j < 6; j++)
						{
							cur_instance->hessian(i, j) += (cur_instance->sd_img[r][c][i] * cur_instance->sd_img[r][c][j]);
						}
					}
				}
			}
			//calculate the inversed Hessian matrix
			cur_instance->inv_hessian = cur_instance->hessian.inverse();

首先setZero初始化Hessian矩阵，其元素全为0。
然后计算子集ref_subset的Hessian矩阵。这个地方的Hessian矩阵是6x6的，具体计算方式可以看原文。
在这里插入图片描述
其中，
在这里插入图片描述
上面这个公式，原文的解释是：ξ=(Δx, Δy, 1) ^T is the local coordinates of the pixel point in each subset。
可以解释为子集中所有点的局部坐标，对应代码中的x_local和y_local
即，Δx = x_local， Δy = y_local
在这里插入图片描述
在这里插入图片描述
具体推导过程就请各位去看原文了。
有了公式以后，代码就不难理解了。
首先计算:
在这里插入图片描述
于是，
在这里插入图片描述
最后还有一步求和工作，在代码中体现在这一段中

for (int i = 0; i < 6; i++)
{
	for (int j = 0; j < 6; j++)
	{
		cur_instance->hessian(i, j) += (cur_instance->sd_img[r][c][i] * cur_instance->sd_img[r][c][j]);
	}
}

求解Hessian矩阵这一段必须要配合原文才能看懂，所以对原文不熟悉的同学要先肝一下原文。

（4）ICGN迭代

在开始迭代之前，要先初始化。
首先是p向量的初始化
在这里插入图片描述

//get initial guess
			Deformation2D1 p_initial(poi->deformation.u, poi->deformation.ux, poi->deformation.uy,
				poi->deformation.v, poi->deformation.vx, poi->deformation.vy);

这里的初值是通过粗匹配获得的。
然后初始化迭代参数，

			//IC-GN iteration
			int iteration_counter = 0; //initialize iteration counter
			Deformation2D1 p_current, p_increment;
			p_current.setDeformation(p_initial);
			float dp_norm_max, znssd;
			Point2D local_coor, warped_coor, global_coor;

这里的iteration_counter记录了迭代次数。
Deformation2D1 p_current和p_increment代表着目前的p和Δp。其中，Δp如下。
在这里插入图片描述
在p_current.setDeformation(p_initial)中，

void Deformation2D1::setDeformation(Deformation2D1& another_deformation)
	{
		u = another_deformation.u;
		ux = another_deformation.ux;
		uy = another_deformation.uy;
		v = another_deformation.v;
		vx = another_deformation.vx;
		vy = another_deformation.vy;

		setWarp();
	}
	void Deformation2D1::setWarp()
	{
		warp_matrix(0, 0) = 1 + ux;
		warp_matrix(0, 1) = uy;
		warp_matrix(0, 2) = u;
		warp_matrix(1, 0) = vx;
		warp_matrix(1, 1) = 1 + vy;
		warp_matrix(1, 2) = v;
		warp_matrix(2, 0) = 0.f;
		warp_matrix(2, 1) = 0.f;
		warp_matrix(2, 2) = 1.f;
	}

p_current被设置为p_initial，作为初始迭代向量。
同时，setWarp()中设置了形变矩阵，如下图的左半部分
在这里插入图片描述
接下来是重头戏，迭代过程。其整体结构如下：

do
{
	iteration_counter++;
	//reconstruct target subset
	......
	//calculate error image
	......
	//calculate ZNSSD
	.......
	//calculate numerator
	.......
	//calculate dp
	.......
	//update warp
	......
	//update p
	......
	//check convergence
	......
} while (iteration_counter < stop_condition && dp_norm_max >= conv_criterion);

在分析代码之前，还是要把整个ICGN匹配策略的过程搞懂。
![在这里插入图片描述](https://img-blog.csdnimg.cn/3d98ccfaf163453898c56cef9e077374.png

下面将逐段解析源码，首先是reconstruct target subset

				//reconstruct target subset
				for (int r = 0; r < subset_height; r++)
				{
					for (int c = 0; c < subset_width; c++)
					{
						int x_local = c - subset_radius_x;
						int y_local = r - subset_radius_y;
						local_coor.x = x_local;
						local_coor.y = y_local;
						warped_coor = p_current.warp(local_coor);
						global_coor = cur_instance->tar_subset->center + warped_coor;
						cur_instance->tar_subset->eg_mat(r, c) = tar_interp->compute(global_coor);
					}
				}
				float tar_mean_norm = cur_instance->tar_subset->zeroMeanNorm();

前面也说过，Δx = x_local, Δy = y_local，于是warped_coor通过warp()函数算出来。
warp()成员函数的定义如下：

	Point2D Deformation2D1::warp(Point2D& location)
	{
		Eigen::Vector3f point_vector;
		point_vector(0) = location.x;
		point_vector(1) = location.y;
		point_vector(2) = 1.f;

		Eigen::Vector3f warped_vector = warp_matrix * point_vector;

		Point2D new_location(warped_vector(0), warped_vector(1));
		return new_location;
	}

其中point_vector即[Δx, Δy, 1]^T，完全符合上面W(ξ; p)的公式右半部分。
得到W(ξ; p)后，还要更新该点的全局坐标global_coor。
global_coor = cur_instance->tar_subset->center + warped_coor;
然后，cur_instance->tar_subset->eg_mat(r, c) = tar_interp->compute(global_coor);
这句通过插值计算出tar_subset在形变以后的亚像素级的值。compute()不再展开。

接下来是计算znssd，根据公式来计算ZNSSD
在这里插入图片描述

公式简化一下就是：
在这里插入图片描述
等式后面可以化简成下式：

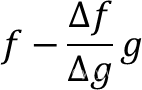
在这里插入图片描述
把 在这里插入图片描述当做一个整体，假设为h(x)，则上式的上半部分就是h(x)二范数的平方。
推导过程理清楚后，来看代码。

//calculate error image
cur_instance->error_img = cur_instance->tar_subset->eg_mat * (ref_mean_norm / tar_mean_norm)
					- (cur_instance->ref_subset->eg_mat);
//calculate ZNSSD
znssd = cur_instance->error_img.squaredNorm() / (ref_mean_norm * ref_mean_norm);

第一条calculate error image计算的error_img，其实就是在这里插入图片描述，为什么要加一个负号呢，在后面会解释。这里因为有平方，所以加不加负号结果是一样的。
再看第二条calculate ZNSSD，error_img.squaredNorm()计算的就是二范数的平方，而ref_mean_norm就是Δf。这样就对上简化后的公式了。

接下来要计算Δp了，calculate numerator也是为了calculate dp，代码中的dp就是Δp。

//calculate numerator
float numerator[6] = { 0.f };
for (int r = 0; r < subset_height; r++)
{
	for (int c = 0; c < subset_width; c++)
	{
		for (int i = 0; i < 6; i++)
		{
			numerator[i] += (cur_instance->sd_img[r][c][i] * cur_instance->error_img(r, c));
		}		
	}
}
//calculate dp
float dp[6] = { 0.f };
for (int i = 0; i < 6; i++)
{
	for (int j = 0; j < 6; j++)
	{
		dp[i] += (cur_instance->inv_hessian(i, j) * numerator[j]);
	}
}
p_increment.setDeformation(dp);

先看原文推导的公式。
在这里插入图片描述
其中的Hessian矩阵、在这里插入图片描述都是已知的，numerator计算的就是Hessian矩阵后面一坨。
第二个X后面的部分简化一下，可以写成
在这里插入图片描述
我的理解是，由于ICGN的诸多假设，f和g的平均值相近可以约掉。再把Hessian矩阵前面的负号代入，就得到了上面提及的在这里插入图片描述。
于是，公式中所有的值都得到了，现在结合代码来看。
numerator[i] += (cur_instance->sd_img[r][c][i] * cur_instance->error_img(r, c));
这句其实就是在这里插入图片描述
循环过程就是求和。

float dp[6] = { 0.f };
for (int i = 0; i < 6; i++)
{
	for (int j = 0; j < 6; j++)
	{
		dp[i] += (cur_instance->inv_hessian(i, j) * numerator[j]);
	}
}

这一段是Hessian矩阵乘以上面计算的结果。
至此，Δp就计算完成了。
得到Δp后，还要更新W和p
W的更新如下

//update warp
p_current.warp_matrix = p_current.warp_matrix * p_increment.warp_matrix.inverse();

是根据公式来计算的
在这里插入图片描述
最后更新一下p，计算一下Δp的模，如果Δp小于终止条件就停止运算，超过了规定的步数也停止计算。
最后输出结果：

//store the final result
			poi->deformation.u = p_current.u;
			poi->deformation.ux = p_current.ux;
			poi->deformation.uy = p_current.uy;
			poi->deformation.v = p_current.v;
			poi->deformation.vx = p_current.vx;
			poi->deformation.vy = p_current.vy;

			//save the parameters for output
			poi->result.u0 = p_initial.u;
			poi->result.v0 = p_initial.v;
			poi->result.zncc = 0.5f * (2 - znssd);
			poi->result.iteration = (float)iteration_counter;
			poi->result.convergence = dp_norm_max;

到这里，整个分析就结束了。这里面还有许多没有搞清楚的细节，希望大佬们能指出我的错误。同学们有问题可以跟我讨论一下，共同进步！

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
OpenFeign的理解和使用
类与对象（三）
解决linux下vim中文乱码的方法
常见前端基础面试题（HTML,CSS,JS）（三）
Git 分布式版本控制系统
MATLAB中head函数用法
计算机端口的安全知识大全，整的明明白白！_哪些端口可以随便使用
王爽著的《汇编语言》第3版笔记
spring-amqp与SpringBoot整合
（附项目源码）Java开发语言，springboot汽车服务管理系统 _580，计算机毕设程序开发+文案（LW+PPT）
;