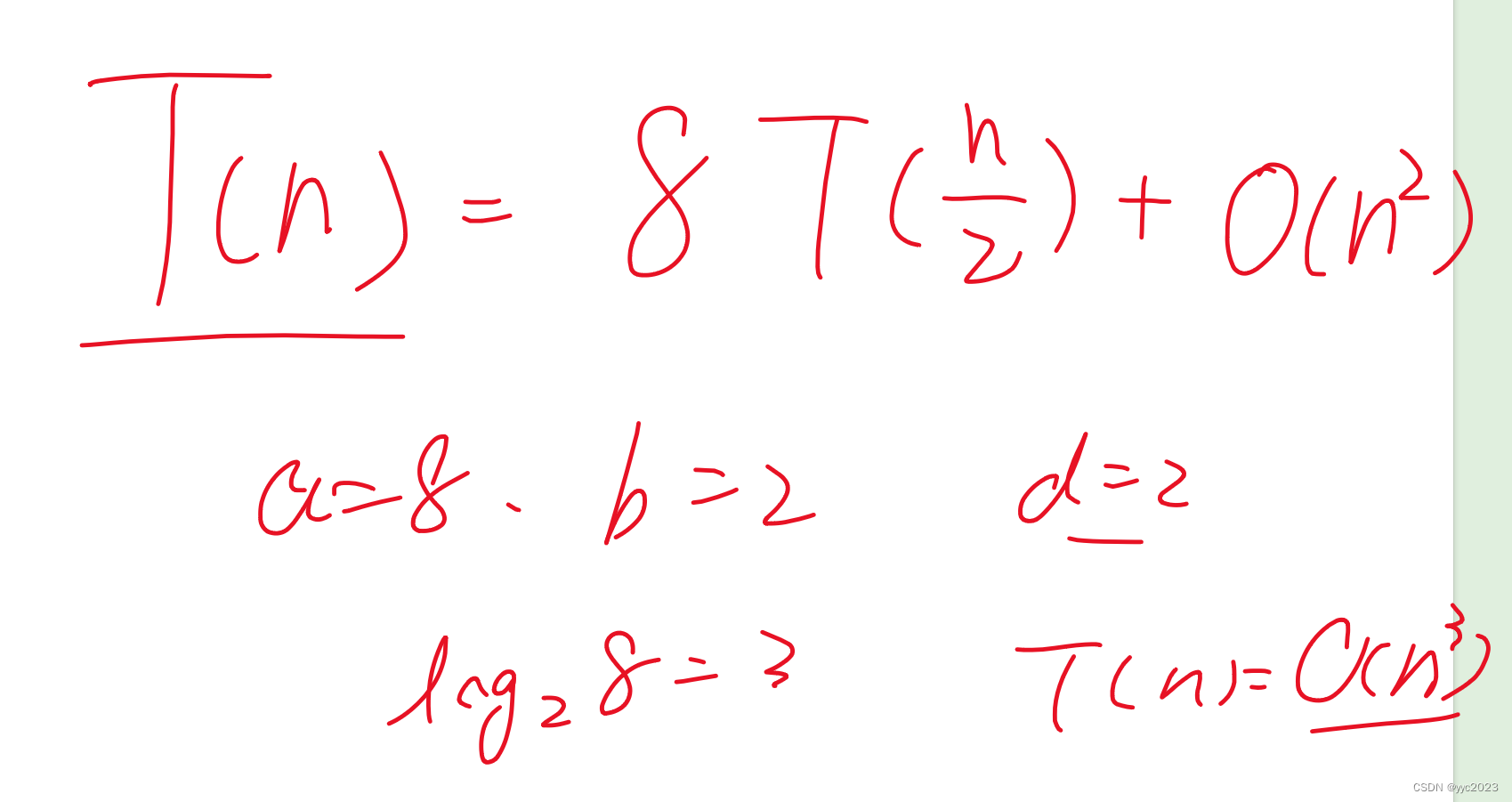2024春期末考题回忆

• 程序题：矩阵快速幂；斐波那契数列的记忆化搜索解法；一个数列中第K小的数，要求时间复杂度为O（n）
• 简答题：主定理公式以及各个参数意义，$lo{g}_{b}a$和d进行比较的意义；a的n次幂的前K项和的递推（要求时间复杂度为$n^3\log n$）。
• 选择题：当代计算机一秒内执行$10^8$条基本语句；双向广度优先搜索是哪个级别的优化（算法）；快速排序有多少种输入，达到$n^2$复杂度的输入有几种；状态变量可以是？；在开关灯游戏中，多少种状态？

一些概念
（理解，不用背）

• 当代计算机一秒内可执行$10^8$条基本语句。

• 算法的时间复杂度是一个函数，修饰一段代码或算法，由问题的输入规模确定，也即执行的基本语句数。（输入规模为问题自变量，从严谨的角度来看，问题的输入规模由输入数据的内存规模来定义，而非由一个值来定义）
  O：关注重要部分；保留增长最快的部分。（O是时间复杂度记号）
  常见的大O运行时间：
  O($logn$)，对数时间，如二分查找
  O(n)，线性时间，如简单查找
  O($n\ast logn$)，如快速排序
  O($n^2$)，如选择排序 O(n!)，如旅行商问题

• 算法的判定问题：判断一个问题的解是否存在；优化问题：找到问题的最优解。面对一个问题，先判断是判别问题还是优化问题，然后找到解空间：什么是可行解，最优解？

• 状态是对可计算问题的一种建模；状态转移是状态通过操作变成另一个状态；状态变量是状态变化的不同取值表示；价值函数，用以衡量当前状态的一个状态到值的映射，该值会伴随着状态转移而更新，该值可以是：布尔值、整数、实数等。
  状态空间是一个图，不是由点和边组成，是由状态和状态转移组成。

• 解决问题的四个层次——问题，模型，算法，代码。时间复杂度与问题规模与基本语句有关，是修饰算法级别的量。
  快速傅里叶变换优化了哪个环节？是问题级别的优化。
  快速排序的时间复杂度：O($n\log n$)；快速排序是原位排序，不会占用额外内存。

• 为什么二分代码要用左闭右开区间？因为闭区间在判断空集时有弊端；而开区间在区间拼接时有弊端；因此半开半闭区间有优势——因此对于二分代码，要用左闭右开区间

• 动态规划：在给定约束条件下找到最优解，在问题可分解为彼此独立且离散的子问题时，可使用动态规划解决。每种动态规划解决方案都涉及网格，单元格中的值通常就是要优化的值，每个单元格都是一个子问题。

练习题（看网站提供的题解思路）：
https://www.luogu.com.cn/contest/166636#problems；https://www.luogu.com.cn/contest/175291

!!!很可能会考的：二分，矩阵快速幂，DFS,BFS

矩阵快速幂算法

通常用于解决斐波那契数列等递归关系问题，核心思想是将幂次分解为二进制形式，通过平方和乘法快速计算结果。（这个要能手写下来）

可将斐波那契数列的时间复杂度降为O（$\log n$）

求矩阵幂前K项和的思路

代码

#include <bits/stdc++.h>
using namespace std;

class Matrix{
public:
    vector<vector<int>> mat;
    int rows, cols;

    Matrix(int r, int c){
        rows = r;
        cols = c;
        mat = vector<vector<int>>(rows, vector<int>(cols, 0));
    }

    int& operator()(int i, int j){
        return mat[i][j];
    }

    Matrix operator*(const Matrix& other)const {
        Matrix res(rows, other.cols);
        for(int i = 0; i < rows; i++){
            for(int j = 0; j < other.cols; j++){
                for(int k = 0; k < cols; k++){
                    res(i, j) += mat[i][k] * other.mat[k][j];
                }
            }
        }
        return res;
    }

    void print() const{
        for(const auto &row : mat){
            for(const auto &val : row){
                cout << val << " ";
            }
            cout << endl;
        }
    }
};

Matrix QuickPow(Matrix A, int n){
    if(n==1) return A;
    Matrix half = QuickPow(A, n/2);
    if(n%2 == 1) return A * half * half;
    else return half * half;
}

int F(int n){
    if(n<=2) return 1;
    Matrix A(2,2);
    A(0,0) = 1;
    A(0,1) = 1;
    A(1,0) = 1;
    A(1,1) = 0;
    A = QuickPow(A, n-2);
    return A(0,0)+A(0,1);
}
int main() {
    int n;
    cin >> n;
    cout << F(n) << endl;
    return 0;

}

记忆化搜索

原理：将函数调用的结果存储起来，适用于递归算法

//计算斐波那契数列
int f(int n){
    if(a[n]>0)
        return a[n];
    if(n<=2)
        return 1;
    return a[n] = f(n-1)+f(n-2);

}

快速排序

原理：通过选择一个基准元素，将数组分为两部分，一部分小于基准，另一部分大于基准，然后对这两部分递归进行排序。
伪代码

function quickSort(arr):
    if length of arr <= 1:
        return arr

    pivot = arr[length of arr // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]

    return quickSort(left) + middle + quickSort(right)

 //zjy版  
// 快速排序函数  
void quicksort(vector<int>& a, int l, int r) {   
    if (r - l <= 0) { // 如果区间内没有元素或只有一个元素，则无需排序  
        return;  
    }  
    int pivot = a[l]; // 选择第一个元素作为基准值  
    int s = 0; // 用于记录小于基准值的元素数量  
    for (int i = l + 1; i < r; i++) {  
        if (a[i] < pivot) {  
            s++;  
        }  
    }  
    int p = l + s; // p是小于基准值的元素应该放置的位置  
    swap(a[l], a[p]); // 将基准值放到正确的位置  
  
    // 三路划分，但在这个实现中只使用了两路划分  
    int i = l, j = p + 1;  
    while (i < p && j < r) {  
        while (i < p && a[i] < pivot) i++;   
        while (j < r && a[j] >= pivot) j++;  
        if (i < p && j < r) {  
            swap(a[i], a[j]);  
        }  
    }  
  
    // 递归对基准值左右两侧的子数组进行排序  
    quicksort(a, l, p);  
    quicksort(a, p + 1, r);  
}  
  
int main() {  
    int n;  
    while (cin >> n) { // 读取要排序的整数数量  
        vector<int> a(n);  
        for (int i = 0; i < n; i++) {  
            cin >> a[i]; // 读取整数并存储到vector中  
        }  
  
        // 调用快速排序函数  
        quicksort(a, 0, n); // 注意：这里应该是n-1，因为数组索引是从0到n-1  
  
        // 输出排序后的数组  
        for (int i = 0; i < n; i++) {  
            cout << a[i] << " ";  
        }  
        cout << endl;  
    }  
    return 0;   
}  
   
// 另外，对于基准值的选择和数组的划分，有很多优化策略，如随机选择基准值、三数取中等。

归并排序

原理：将数组分成两半，分别进行排序，然后合并这两部分。这个过程递归进行，直到每部分的长度为1，最后进行合并。
伪代码

function mergeSort(arr):
    if length of arr <= 1:
        return arr

    middle = length of arr // 2
    left = arr[0:middle]
    right = arr[middle:length of arr]

    left = mergeSort(left)
    right = mergeSort(right)

    return merge(left, right)

function merge(left, right):
    result = []
    while left is not empty and right is not empty:
        if left[0] <= right[0]:
            append left[0] to result
            left = left[1:]
        else:
            append right[0] to result
            right = right[1:]

    while left is not empty:
        append left[0] to result
        left = left[1:]

    while right is not empty:
        append right[0] to result
        right = right[1:]

    return result

例题:https://www.luogu.com.cn/problem/P1908

//求逆序对
#include <iostream>
#include <vector>
using namespace std;

long long mergeAndCount(vector<long long>& arr, vector<long long>& temp, int left, int mid, int right) {
    int i = left;    // 左子数组的起始索引
    int j = mid + 1; // 右子数组的起始索引
    int k = left;    // 临时数组的起始索引
    long long inv_count = 0;

    // 合并两个子数组并统计逆序对
    while ((i <= mid) && (j <= right)) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
            inv_count += (mid - i + 1);
        }
    }

    // 复制左子数组的剩余元素
    while (i <= mid)
        temp[k++] = arr[i++];

    // 复制右子数组的剩余元素
    while (j <= right)
        temp[k++] = arr[j++];

    // 将合并后的数组复制回原数组
    for (i = left; i <= right; i++)
        arr[i] = temp[i];

    return inv_count;
}

long long mergeSortAndCount(vector<long long>& arr, vector<long long>& temp, int left, int right) {
    long long inv_count = 0;
    if (left < right) {
        int mid = (left + right) / 2;

        // 递归统计左子数组的逆序对
        inv_count += mergeSortAndCount(arr, temp, left, mid);

        // 递归统计右子数组的逆序对
        inv_count += mergeSortAndCount(arr, temp, mid + 1, right);

        // 合并两个子数组并统计跨子数组的逆序对
        inv_count += mergeAndCount(arr, temp, left, mid, right);
    }
    return inv_count;
}

int main() {
    int n;
    cin >> n;
    vector<long long> arr(n);
    for (int i = 0; i < n; ++i)
        cin >> arr[i];

    vector<long long> temp(n);
    long long inv_count = mergeSortAndCount(arr, temp, 0, n - 1);
    cout << inv_count << endl;

    return 0;
}

DFS 深度优先搜索

一种图遍历算法，沿着一个分支探索到底再回溯，通常使用栈或递归来实现。适用于连通性检测等问题。
伪代码

function DFS(graph, start):
    visited = set()
    stack = [start]

    while stack is not empty:
        node = pop(stack)
        if node not in visited:
            visit(node)
            visited.add(node)
            for neighbor in graph[node]:
                if neighbor not in visited:
                    push(stack, neighbor)

例题 https://www.luogu.com.cn/problem/P1506

#include<bits/stdc++.h>
using namespace std;

int n,m;
int dx[4] = {1,-1,0,0};
int dy[4] = {0,0,1,-1};
int grid[501][501];

void DFS_oibh(int x, int y){
	grid[x][y] = 1;
	
	for(int i = 0; i<=3;++i){
		int newx = x + dx[i];
		int newy = y + dy[i];
		if(newx>0 && newx <= n && newy>0 && newy<=m && grid[newx][newy] == 0 )
			DFS_oibh(newx,newy);
	}
}
int main(){

	char s;
	cin >> n >> m;
	for(int i = 1; i<=n;++i){
		for(int j = 1; j<=m;++j){
			cin >> s;
			if(s == '*') grid[i][j]=1;
			else grid[i][j]=0;
		}
	}
	for(int i = 1; i <= n; ++i){
		if(grid[i][1] == 0) DFS_oibh(i,1);
		if(grid[i][m] == 0) DFS_oibh(i,m);
		
	}
	for(int j = 1; j <= m; ++j){
		if(grid[1][j] == 0) DFS_oibh(1,j);
		if(grid[n][j] == 0) DFS_oibh(n,j);
	}
	int count = 0;
	for(int i = 1; i <= n; ++i){
		for(int j =1; j <= m; ++j){
			if(grid[i][j] == 0) ++count;
		}
	}
	cout << count;
	return 0;
}

BFS广度优先搜索

一种图遍历算法，按层次逐层搜索节点，通常使用队列来实现，适用于查找最短路径等问题。
伪代码

function BFS(graph, start):
    visited = set()
    queue = [start]

    while queue is not empty:
        node = dequeue(queue)
        if node not in visited:
            visit(node)
            visited.add(node)
            for neighbor in graph[node]:
                if neighbor not in visited:
                    enqueue(queue, neighbor)

课件中的开关灯例题

  
// 定义最大状态数，因为每个格子有2种状态（0或1），所以4x4网格总共有2^(4*4)种状态  
const int maxn = (1 << (4 * 4));  
  
// vis数组用于记录每个状态是否已访问过，以及从初始状态到达该状态的步数  
int vis[maxn];  
  
// oper数组用于存储从每个位置点击灯光后得到的新状态  
int oper[4][4];  
  
// 将4x4的字符串网格转换为16位的整数状态  
int get_code_from_string(const vector<string>& s) {  
    int state = 0;  
    for (int i = 0; i < 4; i++) {  
        for (int j = 0; j < 4; j++) {  
            // 左移4位以处理下一个格子，并将当前格子的值（'0'或'1'）添加到状态中  
            state <<= 1;  
            state |= (s[i][j] - '0');  
        }  
    }  
    return state;  
}  
  
// 定义方向的偏移量  
const int di[5] = {0, 0, 0, 1, -1};  
const int dj[5] = {0, 1, -1, 0, 0};  
  
// 预计算从每个位置点击灯光后得到的新状态  
void get_oper() {  
    for (int i = 0; i < 4; i++) {  
        for (int j = 0; j < 4; j++) {  
            vector<string> cur_op(4, "0000"); // 创建一个4x4的字符串网格，所有灯光初始为关闭状态  
  
            for (int k = 0; k < 5; k++) { // 考虑5个方向：上、下、左、右以及自身（通常自身不翻转，但这里可能是为了初始化）  
                int new_i = i + di[k];  
                int new_j = j + dj[k];  
                if (new_i >= 0 && new_i < 4 && new_j >= 0 && new_j < 4) {  
                    // 假设点击(i, j)位置会翻转(new_i, new_j)位置的灯光  
                    cur_op[new_i][new_j] = '1'; // 实际上这里可能应该根据具体情况来决定是'0'还是'1'  
                }  
            }  
            oper[i][j] = get_code_from_string(cur_op); // 将修改后的网格转换为状态，并存储在oper数组中  
        }  
    }  
}  
  
// 使用广度优先搜索来遍历所有可能的状态  
void bfs(int start) {  
    memset(vis, -1, sizeof(vis)); // 初始化vis数组，将所有状态标记为未访问  
    queue<int> q;  
    q.push(start); // 将初始状态加入队列  
    vis[start] = 0; // 初始状态的步数为0  
  
    while (!q.empty()) {  
        int cur = q.front();  
        q.pop();  
  
        for (int i = 0; i < 4; i++) {  
            for (int j = 0; j < 4; j++) {  
                // 通过异或操作获取点击(i, j)后的新状态  
                int new_x = cur ^ oper[i][j];  
                if (vis[new_x] == -1) { // 如果新状态未被访问过  
                    q.push(new_x); // 将新状态加入队列  
                    vis[new_x] = vis[cur] + 1; // 更新到达新状态的步数  
                }  
            }  
        }  
    }  
}  
  
int main() {  
    get_oper(); // 预计算所有操作  
  
    bfs(0); // 从初始状态（所有灯光关闭）开始广度优先搜索  
  
    int maxv = 0, maxi = -1;  
    map<int, vector<int>> m; // 用于统计每个步数可以到达的不同状态数量  
  
    // 遍历所有可能的状态，找到最远步数和对应的状态  
    for (int i = 0; i < maxn;i++) {
		if (vis[i] != -1) { // 如果该状态是可达的
			m[vis[i]].push_back(i); // 将状态及其步数添加到map中
		if (vis[i] > maxv) { // 如果步数大于当前最大步数
			maxv = vis[i]; // 更新最大步数
			maxi = i; // 更新对应的状态
		}
		}
	}
	// 输出最远步数以及对应的状态  
	cout << "Max steps: " << maxv << endl;  
	cout << "State with max steps: ";  
	for (int k = 0; k < 16; k++) {  
	    cout << ((maxi >> k) & 1); // 将状态转回为字符串形式  
	    if (k % 4 == 3 && k != 15) cout << endl; // 每4位换行  
	}  
	cout << endl;  
	
	// 输出每个步数可以到达的不同状态数量  
	for (auto& pair : m) {  
	    cout << "Steps: " << pair.first << ", Number of states: " << pair.second.size() << endl;  
	}  
	
	return 0;

二分查找

!!! 二分是必考
原理：每次比较时，将搜索范围减半，直到找到元素或范围为空。

function binarySearch(arr, target):
    left = 0
    right = length of arr - 1

    while left <= right:
        mid = left + (right-left) // 2   !!!注意这个地方，不是(left+right)/2，而是left + (right-left) /2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1

    return -1

//zjy的版本
  
// 定义一个常量maxn，用于数组的大小，这里假设最多有1e5+5个元素  
const int maxn = 1e5+5;  
// 定义一个全局数组a，用于存储输入的整数  
int a[maxn];  
// 定义全局变量n和k，分别用于存储数组a的长度和需要达到的目标值  
int n, k;  
// 定义全局变量maxL，用于存储数组a中的最大值  
int maxL;  
  
// 定义函数cut，用于计算数组a中所有元素除以L后的和  
int cut(int L) {  
    int s = 0; // 初始化和s为0  
    for(int i = 0; i < n; i ++) { // 遍历数组a  
        s += a[i] / L; // 累加每个元素除以L的商  
    }  
    return s; // 返回累加和s  
}  
  
// 定义函数bs，用于通过二分查找找到满足cut(L) >= v的最小L值  
int bs(int v) {  
    int l = 1, r = maxL + 1; // 定义二分查找的左右边界  
    while(l < r) { // 当左边界小于右边界时继续查找  
        int mid = l + (r-l)/2; // 计算中间值mid  
        //if(-cut(mid) <= -v) { // 原代码中的比较逻辑是多余的，因为cut函数返回的是非负整数  
        if(cut(mid) >= v) { // 如果cut(mid)的值大于等于目标值v  
            l = mid+1; // 更新左边界为mid+1，继续向右查找  
        } else {  
            r = mid; // 否则更新右边界为mid，向左查找  
        }  
    }  
    return l - 1; // 返回最终查找到的最小L值（注意需要减去1，因为最后l会超出目标值）  
}  
  
int main() {  
    ios::sync_with_stdio(false); // 关闭C++标准库与C标准库的同步，加速输入输出  
    cin >> n >> k; // 读取数组长度n和目标值k  
    maxL = 0; // 初始化maxL为0  
    for(int i = 0; i < n; i ++) { // 遍历数组a  
        cin >> a[i]; // 读取每个元素的值  
        maxL = max(a[i], maxL); // 更新maxL为当前元素和maxL中的较大值  
    }  
    cout << bs(k) << endl; // 调用bs函数，输出满足cut(L) >= k的最小L值  
    return 0; 
}

二分查找的写法很多，以这道题为例
搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

//解法一
public class Solution {

    public int searchInsert(int[] nums, int target) {
        // 不用判断数组为空，因为题目最后给出的数据范围说数组不为空
        int len = nums.length;
        // 特殊判断
        if (nums[len - 1] < target) {
            return len;
        }

        // 程序走到这里一定有 nums[len - 1] >= target，插入位置在区间 [0..len - 1]
        int left = 0;
        int right = len - 1;
        // 在区间 nums[left..right] 里查找第 1 个大于等于 target 的元素的下标
        while (left < right) {
            int mid = (left + right) / 2;
            if (nums[mid] < target){
                // 下一轮搜索的区间是 [mid + 1..right]
                left = mid + 1;
            } else {
                // 下一轮搜索的区间是 [left..mid]
                right = mid;
            }
        }
        return left;
    }
}

//解法二
public class Solution {

    public int searchInsert(int[] nums, int target) {
        int len = nums.length;
        int left = 0;
        int right = len;
        // 在区间 nums[left..right] 里查找第 1 个大于等于 target 的元素的下标
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target){
                // 下一轮搜索的区间是 [mid + 1..right]
                left = mid + 1;
            } else {
                // 下一轮搜索的区间是 [left..mid]
                right = mid;
            }
        }
        return left;
    }
}

//解法三
class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n - 1, ans = n;
        while (left <= right) {
            int mid = ((right - left) >> 1) + left;
            if (target <= nums[mid]) {
                ans = mid;
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return ans;
    }
}

//解法四
class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while(left <= right) {
            int mid = (left + right) / 2;
            if(nums[mid] == target) {
                return mid;
            } else if(nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return left;
    }
}

一些例子
题目：https://www.luogu.com.cn/problem/P2678

//二分，贪心
bool canAchieveMinJump(const vector<int>& distances, int N, int M, int minJump){
    int removeCount = 0;
    int lastPos = 0;

    for(int i = 1; i<=N;++i){
        if(distances[i] -lastPos< minJump){
            removeCount++;
            if(removeCount > M) return false;
        } else {
            lastPos = distances[i];
        }
    }
    return true;
}
int findMaxMinJumpDistance(const vector<int>& distances, int N, int M, int L){
    int left = 1;
    int right = L;
    int result = 0;

    while(left <= right){
        int  mid = left + (right-left) / 2;
        if(canAchieveMinJump(distances, N, M, mid)){
            result = mid;
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }

    return result;
}
int main() {
    int L, N, M;
    cin >> L >> N >> M;

    vector<int> distanceToStart(N+2);
    distanceToStart[0] = 0;
    distanceToStart[N+1] = L;

    for(int i = 1; i <= N;++i){
        cin >> distanceToStart[i];
    }

    sort(distanceToStart.begin(), distanceToStart.end());
    int maxMinJump = findMaxMinJumpDistance(distanceToStart, N, M, L);
    cout << maxMinJump << endl;
    return 0;
}

题目：https://www.luogu.com.cn/problem/P2370

//二分
#include <bits/stdc++.h>
using namespace std;

class USB{
public:
    int p;//最小价值
    int S;//U盘大小
    USB(int _p, int _S): p(_p), S(_S){}
};

class File{
public:
    int w;//文件大小
    int v;//文件价值
};

void findMinConnecterSize(vector<File>& files, USB& usb, int n){
    int maxV = 0;
    for(auto f:files){
        maxV += f.v;
    }
    if(maxV < usb.p) {
        cout << "No Solution!" << endl;
        return;
    }

   int left = 1, right = 1e9, result = -1;
    while(left <= right){
        int mid = left + (right - left) / 2;

        vector<int> dp(usb.S+1, 0);
        for(int i = 0; i < n; ++i){
            if(files[i].w <= mid){
                //j代表当前u盘剩余容量,dp[j]表示当前剩余容量 j 下的最大价值
                for(int j = usb.S; j >= files[i].w; --j){
                    dp[j] = max(dp[j], dp[j-files[i].w] + files[i].v);
                }
            }
        }

        bool found = false;
        for(int j = 0; j<=usb.S; ++j){
            if(dp[j] >= usb.p){
                found = true;
                break;
            }
        }

        if(found){
            result = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    
    if(result == -1){
        cout << "No Solution!" << endl;
    } else {
        cout << result << endl;
    }
}


int main() {
    int n;
    int p, S;

    cin >> n >> p >> S;
    USB usb = USB(p, S);

    vector<File> files(n);
    for (int i = 0; i < n; ++i) {
        cin >> files[i].w >> files[i].v;
    }

    findMinConnecterSize(files, usb, n);

    return 0;
}

分治算法

原理：将一个复杂的问题分解为较小的子问题，递归地解决这些子问题（如果子问题足够小，则直接解决），最后合并其结果得到最终解.

伪代码

function divideAndConquer(problem):
    if problem is small enough:
        return direct solution to problem

    subproblems = divide(problem)
    solutions = []
    for subproblem in subproblems:
        solutions.append(divideAndConquer(subproblem))

    return combine(solutions)

怎么用

归并排序，快速傅里叶变换采用的就是分治算法

背包问题

有一个容量为V的背包，还有n个物体，只要背包的剩余容量大于等于物体体积，那就可以装进背包里。每个物体都有两个属性，即体积w和价值v。
如何向背包装物体才能使背包中物体的总价值最大？

#include <bits/stdc++.h>
using namespace std;
int main() {
    vector<int> w, v;//重量，价值
    vector<int> f;

    int V,n;//容量，物体数
    while(cin >> V >> n){
        w.push_back(0);
        v.push_back(0);
        for(int i = 1; i <= n; i++){
            cin >> w[i] >> v[i];
        }

        f = vector<int>(V+1, 0);
        for(int i = 1; i <= n; i++){
            for(int j = V; j>=w[i];j--){
                f[j] = max(f[j], f[j-w[i]]+v[i]);
            }
        }
        	//输出答案
		int ans = f[V];
		cout << ans << endl;
    }
    return 0;
}