目录
上一篇博客我已经介绍了一些时间复杂度,它的概念,表达方法,有具体的例题来分析(http://t.csdnimg.cn/CVV7v有兴趣的同学可以点这个链接看看时间复杂度),现在来介绍衡量一个算法好坏的另一个复杂度,空间复杂度。
一.空间复杂度概念:
空间复杂度和时间复杂度一样也是一个数学表达式,是对一个算法在运行过程中临时占用储存空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没多大的意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则与时间复杂度类似,也使用大O渐进法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器的信息等)在编译期间就已经确定好了,因此空间复杂度主要通过函数在运行的时候显式申请的额外空间来确定的。
常见的空间复杂度:O(1),O(N),O(N^2)(这个是开辟二维数组时)
二.例子
例子1:
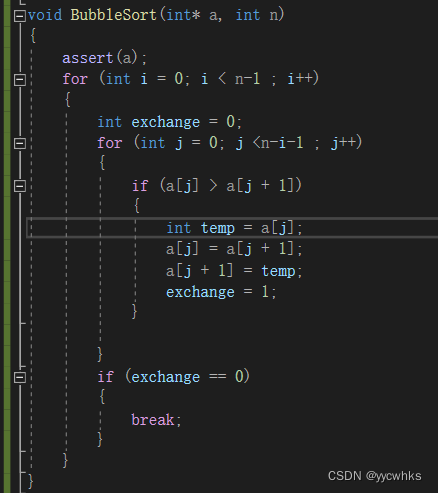
冒泡排序的空间复杂度
答案是很明显是常数个(数组不算空间复杂度,算法中额外开的空间),用大O渐进法表示O(1)
例子2:
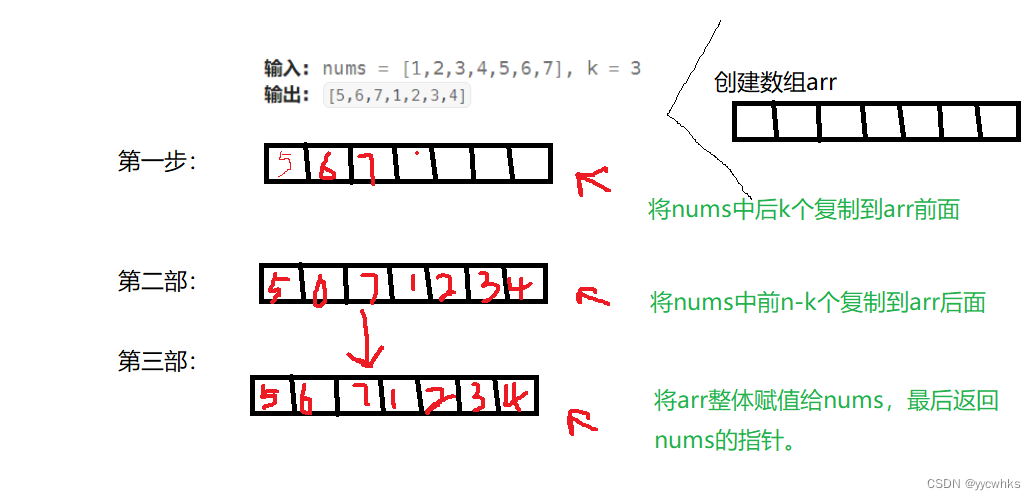
还记得时间复杂度时的例题吗?三段逆置可能第一次想不到,另外一个思路就是创建新数组,用空间换时间的算法。
画图写思路:
例子3:
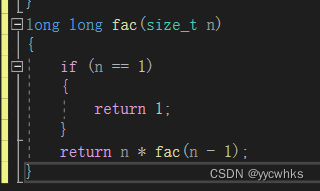
递归阶乘
很简单的例子,空间复杂度为O(N)。
例子4:
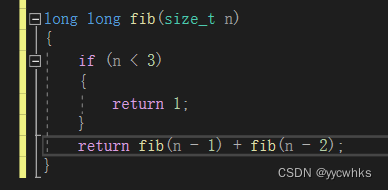
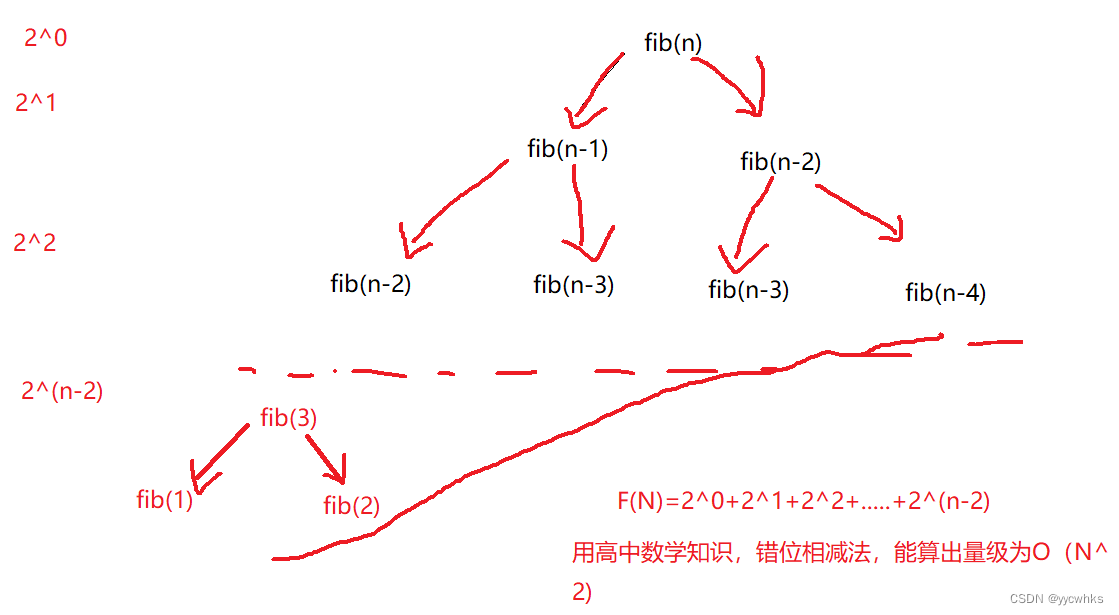
斐波那契数列
思路一:递归解
空想可能有点难度,这里可以借助画图来帮助理解
可以解出空间复杂度为O(N……2)。
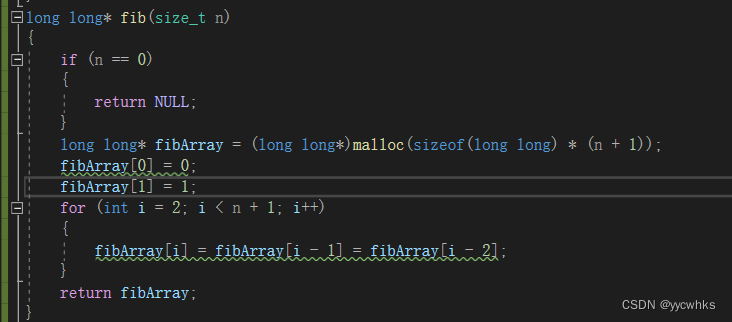
思路二:创数组接收斐波那契数
这里用malloc函数开辟了n+1个变量,空间复杂度O(N);
三.结语:
接着就是链表的学习(顺序表,单链表,双链表已经学过了),哥们会不断进步的。