文章目录
引语:
本篇文章从迭代,递归,再到深搜,由浅入深结合例题介绍。如果是零基础的,建议从头看完,这样到后面更好理解,如果递归学的较好的话也可以跳过前面的递归部分。
在各种算法竞赛或者面试中,总会有一些题目要求我们给出某个问题的各种方案以及方案的个数,对于数量级比较小的题目,我们可以采用枚举之类的暴力解法,但是对于数量级到达n的三次方及以上的题目甚至是阶乘级的题目就要小心了,因为暴力求解很可能超时。
所以,我们可以用试探性解法,当某一条支路提前确定走不通的时候,我们就不必继续向下进行了。也可以理解为“不撞南墙不回头”,或者“先把一条路走到黑”。
虽然看起来比暴力枚举更快一点,但是《算法竞赛入门经典》这本书将这种方法一并归到“暴力求解法”这一章。
回顾
首先,我想先从“逐步生成结果”开始讲起。
刚开始学C语言的时候,我们会学“斐波那契数列”,这就是典型的“逐步生成”思想,也可以理解为迭代。
我相信斐波那契大家肯定很熟悉了,这里就不在介绍了。
解决简单情况下的问题:上楼梯
题意:有一个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶,2阶,3阶。
请实现一个方法,计算小孩有多少种上楼梯的方式。
为了防止溢出,请将结果Mod1000000007。 给定一个正整数,请返回一个数,代表上楼的方式数。保证n小于等于100000.
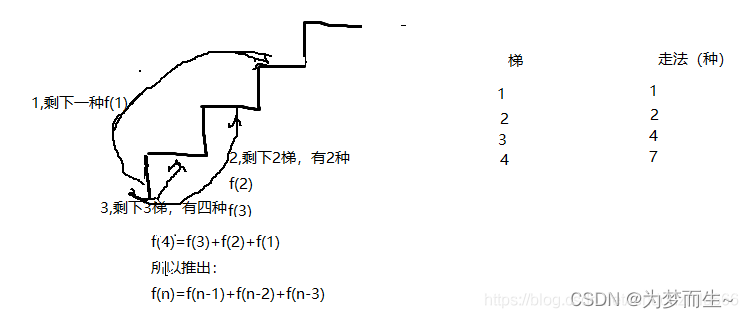
由题意,我们可以做出如下图所示的推理:
递推:
#include<stdio.h>
#define mod 1000000007
int main(){
int x1 = 1, x2 = 2, x3 = 4, n;
long long ans = 0;
scanf("%d",&n);
if(n < 0) ans = 0;
else if(n == 0 || n == 1) ans = x1;
else if(n == 2) ans = x2;
else if(n == 3) ans = x3;
for(int i = 4; i <= n; i++){
int t = x1;
x1 = x2; x2 = x3;
x3 = ((x1+x2)%mod+t)%mod;
ans = x3;
}
printf("%d\n",ans);
return 0;
}
递归:
long f1(int n){
if(n < 0) return 0;
if(n == 0 || n == 1) return 1;
if(n == 2) return 2;
return f1(n-1)%mod + f1(n-2)%mod + f1(n-3)%mod;
}
如果大家数学基础比较好,也可以利用递推公式,直接得出封闭解。由于我数学推理不是很好,在这里就不展示了。
推广到稍微复杂的问题:机器人走方格
有一个X*Y的网格,一个机器人只能走格点且只能向右或向下走,要从左上角走到右下角。
请设计一个算法,计算机器人有多少种走法。
给定两个正整数int x,int y,请返回机器人的走法数目。
保证x+y小于等于12。
由题意我们可以推出:
- 当x或者y为1时,走法都是1种。
- 当x或者y为2,另一个为1时,也就是(1,2)或者(2,1),走法也都是1种。
- 当x和y都为2时,走法是两种 ……
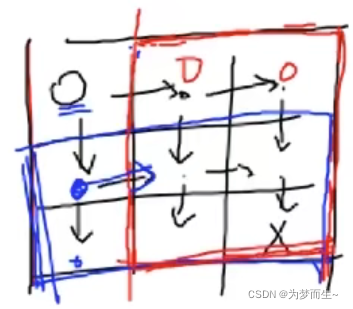
顺着思路往下想,我们可以画出这样一幅示意图:
从这幅图我们可以发现:
- 在
x+y>=3时,当前状态的解都为(x-1,y)状态的解和(x,y-1)的解的和
也就是f(x,y)=f(x-1,y)+f(x,y-1) - 因为在任何一种状态,我们都有两种选择,下或者右,如果现在向下走,那么下一种状态的解即为
(x,y-1)的解,如果向右,那么下一种状态为(x-1,y)的解。
所以,我们同样可以用递推或者递归来写代码~
递推:
建立一个二维数组存放每一个状态对应的解,逐步迭代得到所有解
#include<stdio.h>
int solve1(int x, int y){
int a[x+1][y+1];
for(int i = 1; i <= x; i++) a[i][1] = 1;//当x或y为1时,解法都是一种
for(int i = i; i <= y; i++) a[1][i] = 1;
for(int i = 2; i <= x; i++){
for(int j = 2; j <= y; j++){
a[i][j] = a[i-1][j]+a[i][j-1]; //利用递推关系迭代出所有的解
}
}
return a[x][y];
}
int main(){
int x,y;
scanf("%d%d",&x,&y);
printf("%d\n",solve1(x,y));
return 0;
}
递归:
int solve2(int x, int y){
if(x == 0 || y == 0 || x == 1 || y == 1) return 1;
return solve2(x-1,y)+solve2(x,y-1);
}
由以上两道例题我们发现,递推和递归都是对于需要迭代问题的解法
区别在于:递推是正着思考正着写,递归是正着思考倒着写
递归对于这类问题的思考的锻炼是非常有帮助的。
还有一道更难一点的题:硬币表示(点击阅读我的另一篇文章)
逐步生成结果之非数值形
以上两个问题都是与算数有关的,都是可以直接通过算式解出来的,但是有一类问题也可以通过递归或递推,但是无法通过以上形式算出的,我们称之为非数值类型。
我们先来看一道题:合法括号
- 问题描述:
输入括号对数,输出所有的合法组合,比如输入1,输出"()“,输入3,输出”()()(), (()()), ()(()), (())(),
((()))"。
- 思路分析:
面对这种问题,其实一开始想通如何使用递归是不太容易的,不妨一一列举出来,发现其相应的规律。可以发现,增加一个单位,则都会在其上一个集合上每个元素的左面、右面和整体的外面加上一层括号。那么就会产生大量的重复元素,所以,我们使用Set集合进行去重。
代码:
#include<iostream>
#include<string>
#include<set>
using namespace std;
set<string> parentheis(int n){
set<string> s_n;
if(n == 1){ //出口:当n为1时,也就是最开始,只有一个括号
s_n.insert("()");
return s_n;
}
set<string> s_n_1 = parentheis(n-1);//递归思想:假设程序已经帮我们做好了n-1个状态,我们只需在此基础上生成当前状态即可
for(set<string>::iterator it = s_n_1.begin(); it != s_n_1.end(); it++){
s_n.insert("()"+(*it));
s_n.insert((*it)+"()");
s_n.insert("("+(*it)+")");
}
return s_n;
}
int main(){
int n;
cin >> n;
set<string> s = parentheis(n);
for(set<string>::iterator it = s.begin(); it != s.end(); it++){
cout << *it << " ";
}
cout << endl;
return 0;
}
C++和Java都有set,但是对于set 的迭代方式等稍有区别
类似的问题还有子集生成和全排列,大家也可以到我们文章中阅读
引出DFS
对于一些数据量级比较大的题目,我们可能无法通过一一列举来迭代出全部的情况。
例如下面这道题:
数独游戏
你一定听说过“数独”游戏。
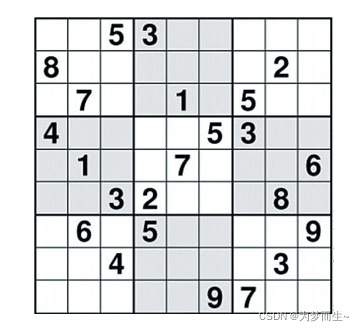
如下图所示,玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个同色九宫内的数字均含1-9,不重复。
数独的答案都是唯一的,所以,多个解也称为无解。
本图的数字据说是芬兰数学家花了3个月的时间设计出来的较难的题目。但对会使用计算机编程的你来说,恐怕易如反掌了。
本题的要求就是输入数独题目,程序输出数独的唯一解。我们保证所有已知数据的格式都是合法的,并且题目有唯一的解。
格式要求,输入9行,每行9个数字,0代表未知,其它数字为已知。 输出9行,每行9个数字表示数独的解。
就像是这道题,如果把所有的情况从第一个列举到最后一个,恐怕计算机无法完成。
解题思路:
- 对于每一个方格,无非就是两种状态:已经有数,没数。
- 对于已经有数的方格,直接看下一个空即可
- 对于需要填的位置,我们可以在填每一个数之前检查一下要放的这个数是否合法。这一个状态完成之后继续判断下一个状态。也就是从第一个需要填的位置开始检查,从1开始试数,如果符合题目条件,那么继续递归进行下一个状态,如果不符合,试2……一直到9。如果都不合法,那么无解。
- 这样做有一个好处:每成功的放下一个数,都能保证当前状态是符合题目条件的,所以接下来的遍历,无需检查下面要放的数是否跟前面的数冲突,只需要检查是否与后面的数相冲突,间接的节省了时间。
- 如果当前解可行,那么继续递归下一种状态,也就是说,一条路只要走到黑,递归到最后一个需要填放的位置之后,就找到了一组解,就可以退出了
根据这个思路我们可以设计出这样的代码:
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
bool check(char table[9][9], int x, int y, int i){
//检查每一行每一列,每一个小九宫格
for(int l = 0; l < 9; l++){
if(table[x][l] == ('0'+i)) return false;
if(table[l][y] == ('0'+i)) return false;
}
for(int l = (x/3)*3; l < (x/3+1)*3; l++){
for(int m = (y/3)*3; m < (y/3+1)*3; m++){
if(table[l][m] == ('0'+i)) return false;
}
}
return true;
}
void print(char table[9][9]){
//打印输出
for(int i = 0; i < 9; i++){
for(int j = 0; j < 9; j++){
cout << table[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
void dfs(char table[9][9], int x, int y){
if(x == 9){ //此时所有的格子都已经走完
print(table);
exit(-1);
}
if(table[x][y] == '0'){ //虚位以待
for(int i = 1; i <= 9; i++){ //对于此时的状态,检测此位置适合填1-9中的哪个数
if(check(table,x,y,i)){ //检测这个数是否可以填入
table[x][y] = i+'0';//填入
dfs(table, x+(y+1)/9, (y+1)%9);//再搜索下一个状态
// print(table);
}
}
table[x][y] = '0'; //回溯
}else{ //如果这里有数,填下一个状态
dfs(table, x+(y+1)/9, (y+1)%9);
}
}
int main(){
char table[9][9];
for(int i = 0; i < 9; i++){
for(int j = 0; j < 9; j++){
cin >> table[i][j];
}
}
cout << endl;
// print(table);
dfs(table,0,0);
return 0;
}
/*
测试集:
0 0 5 3 0 0 0 0 0
8 0 0 0 0 0 0 2 0
0 7 0 0 1 0 5 0 0
4 0 0 0 0 5 3 0 0
0 1 0 0 7 0 0 0 6
0 0 3 2 0 0 0 8 0
0 6 0 5 0 0 0 0 9
0 0 4 0 0 0 0 3 0
0 0 0 0 0 9 7 0 0
结果:
1 4 5 3 2 7 6 9 8
8 3 9 6 5 4 1 2 7
6 7 2 9 1 8 5 4 3
4 9 6 1 8 5 3 7 2
2 1 8 4 7 3 9 5 6
7 5 3 2 9 6 4 8 1
3 6 7 5 4 2 8 1 9
9 8 4 7 6 1 2 3 5
5 2 1 8 3 9 7 6 4
*/
当然我写的代码有缺点,二维数组可以设为全局变量,这样可以避免递归时过多的空间开销,节省空间复杂度。
- 以上的核心就是
void dfs(char table[9][9], int x, int y),这就是所谓的深搜思想。也就是前面的解题思路,在这里就不过多赘述了。 - 关键:1.找到入口条件;2.如何试解;3.判断是否需要回溯(后面会讲)4.找到出口条件
下面我们再用两道题深入理解掌握DFS
部分和
题目描述:
给定整数序列a1,a2,…,an,判断是否可以从中选出若干数,使它们的和恰好为k.
1≤n≤20;-10 ^ 8 ≤ai≤ 10 ^ 8;-10 ^ 8 ≤k≤ 10 ^ 8
输入
4
1 2 4 7
13
输出
Yes (13 = 2 + 4 + 7)
解题思路:
这道题跟子集生成的解题方法非常类似,只是这道题不需要遍历所有的子集,只需要试探选择或不选某一个值,如果选择的数的和符合条件就退出打印即可。
- 首先建立一个空集合,初始化后进入
- 对于当前的状态,我们看是否要数组中cur下表所指的数。无非就两种选择,要或不要。
- 如果不要,把现有状态传入继续递归下一个状态即可
- 如果要,把当前数加入到list中,传入list还有k减去选择的数后剩下的数,继续递归下一个状态,直到家和等于k,或者一条路走到黑之后返回到平行状态。
- 如果退回到平行状态,记得回溯,remove掉上一个状态加入的元素。
注意:这种方法每选一个数,递归下一个状态时,就要把k减去这个数,直到k减到0,也就找到了一组解。
由以上思路可以得到以下代码:
#include<iostream>
#include<list>
#include<algorithm>
using namespace std;
int n,k;
void printList(list<int> res){
cout << "Yes (" << k << "=";
for(list<int>::iterator it = res.begin(); it != res.end(); it++){
cout << *it;
if(++it != res.end())
cout << "+";
--it;
}
cout << ")" << endl;
}
void dfs(int a[], int k, int cur, list<int> ints){
//退出条件
if(k == 0){
printList(ints);
exit(-1);
}
if(k < 0 || cur >= n) return; //要求的和是小于零的数或者当前迭代次数超出数组上界,返回找平行状态
dfs(a, k, cur+1, ints);//不要当前的数
//要当前的数
ints.push_back(a[cur]);
dfs(a, k-a[cur], cur+1, ints);
ints.remove(a[cur]); //回溯
}
int main(){
cin >> n;
int a[n];
for(int i = 0; i < n; i++)
cin >> a[i];
cin >> k;
list<int> ints;
dfs(a,k,0,ints);
return 0;
}
除了dfs,这道题还可以用二进制法,把所有的子集从头到尾判断一遍,如果符合题目规定,打印退出。
是否需要回溯
判断是否需要回溯,首先我们需要理解dfs的原理,就是试探性的判断出一组解!
开始递归之后,每次递归产生的“半成品”我们称为一个状态。
如果还可以继续向下递归,那么下一“半成品”称为下一个状态
如果下一个状态无法继续向下递归而需要返回,到当前状态之后继续试解,我们称此为平行状态
这类似于二叉树的孩子结点、父节点和兄弟结点的关系。
那么什么时候需要回溯?
- 我们看以上这个例子,如果某状态无法向下继续递归而返回找他的平行状态,那么链表的最后一个元素也就不能加入到答案中,那么这个时候就需要手动删除最后一个元素继续找平行状态。这个时候就需要回溯。
- 如果在找平行状态时,能通过控制数组下标等方法,覆盖或者删除刚刚的元素,那么这个时候就不需要回溯。甚至有时候上一个状态在修改之后,由于我们之后要做的操作需要用到修改之后的数,这个时候坚决不能回溯。
例如水洼数这个题,就是典型的不能回溯的例子。
回溯的经典例题就是n皇后问题,这个题跟前面的思路还差不多,我之前写过的文章有2n皇后问题。
我对于“剪枝”的理解
其实我们在判断当前状态时,就已经用到了剪枝的思想。
- 像是第一道例题“数独游戏”,我们在填入操作之前,已经进行了一个
check(table,x,y,i)来查看这个数是否可以填入,则不需要填入之后再判断是否合法,浪费一次递归。 - 只是这样一个check操作的时间复杂度还可以优化,对于某些题,甚至可以优化为O(1)的时间复杂度,即空间换时间。
- 像是第二道例题,这里没有用到剪枝,因为这里无法用这个方法,此种思路只能是顺着一条路走到头,直到用完数组中所有的数仍无解,或者中间无法递归而返回。
综合这两道例题,我们足以判断什么时候可以用剪枝和回溯。
总结
任何抛开例题空讲算法都是无稽之谈,所以我特地在这里结合例题,并且由浅入深的讲解了dfs。
由于该算法是以递归为基础,所以前半部分都是递归,只有把基础打牢,我们才有可能学好进阶。
- 总的来说,本篇文章主要有两部分
- 逐步生成结果(分为数值型和非数值型)。一道题只要是有明确的递推关系,都可以用迭代的形式来写,递归形式可以更好的锻炼思维能力。如果用递推,它的起止范围是比较明确的;如果是递归,它迭代的层数和宽度是比较明确的。(主要例题:走楼梯、机器人走方格、硬币表示、合法括号、子集生成、全排列)
- DFS+回溯+剪枝。这一类问题,往往解的空间很大(往往是阶乘级别的),要在所有可能性中找到答案,必须进行试探,尝试往前走一步,走不通再退回来。(主要例题:数独游戏、部分和、水洼数、n皇后问题、素数环、困难的串)
参考文章:
深搜(DFS)
上楼梯(cc150)
数独游戏