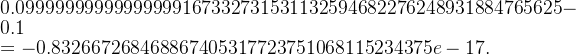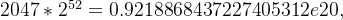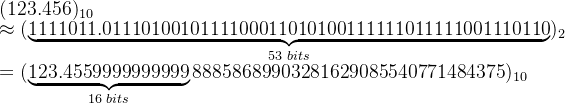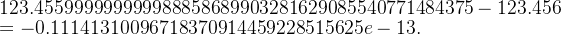摘要  本节介绍浮点数的表示误差。

       浮点数的表示误差是指十进制数转换成二进制数时产生的误差。双精度下，二进制数有 53 位二进制有效数字（称为 bit）, 并且 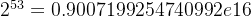 有 16位整数，所以很多时候浮点数具有16位左右正确数字。

例1.  双精度下，十进制的 0.1 变成了含有 53 位有效数字的二进制数，而该二进制数实际等于另外一个十进制数：

于是，产生了表示误差（即二者的差）：

另外，在理论上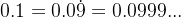，，所以上式有连续 16 个 9。

        双精度下，机器能表示的非负浮点数数目不会超过

用其表达C++的（最小值, 最大值）区间

范围内的的实数，很大的概率会产生表示误差。

       再比如 123.456 变为：

其表示误差为：

       其实，通过分析下面类型的十进制数，我们可以看到，当小数转换成二进制数时，成为无穷位的概率极大。

1.  9个数中，只有   1个 数的二进制数是有限位的，其余 8个数的二进制数均为无穷位；

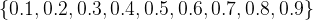
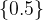
2.  90个数中，只有  3个数的二进制数是有限位的，其余 87个数的二进制数均为无穷位；

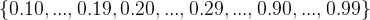
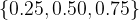
3.  ...

       从上可知，上述小数转换成二进制数时，成为无穷位的概率非常高；这样，对于该类数来说，二进制数被截断的概率极大。因此产生表示误差的可能性也极大，从而从统计学的角度看，产生表示误差的概率是接近100%。