总目录

一、 凸优化基础（Convex Optimization basics）

1. 凸优化基础（Convex Optimization basics）

二、 一阶梯度方法（First-order methods）

1. 梯度下降（Gradient Descent）
2. 次梯度（Subgradients）
3. 近端梯度法（Proximal Gradient Descent）
4. 随机梯度下降（Stochastic gradient descent）

三、对偶

1. 线性规划中的对偶（Duality in linear programs）
2. 凸优化中的对偶（Duality in General Programs）
3. KKT条件（Karush-Kuhn-Tucker Conditions）
4. 对偶的应用及拓展（Duality Uses and Correspondences）
5. 对偶方法（Dual Methods）
6. 交替方向乘子法（Alternating Direction Method of Multipliers）

Introduction

上一节我们提到了强对偶，即原问题的最优值与对偶问题的最优值相等。下面我们需要解决怎样找到优化问题的最优解。而KKT条件就是最优解需要满足的条件。

KKT条件

给定一个一般性的优化问题：
$$\begin{array}{rl}\underset{x}{\min }& f(x)\\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& h_i(x)\le 0,i=1,...,m\\ & l_i(x)=0,j=1,...,r\end{array}$$

KKT条件（Karush-Kuhn-Tucker conditions or KKT conditions）定义为：

• 稳定性条件：$$0\in {\partial }_x(f(x)+\sum _{i=1}^m{u}_i{h}_i(x)+\sum _{j=1}^r{v}_j{l}_j(x))$$
• 互补松弛性：$$u_i\cdot h_i(x)=0\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}i$$
• 原问题可行域：$$h_i(x)\le 0,l_i(x)=0\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}i,j$$
• 对偶问题可行域：$$u_i\ge 0\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}i$$

充分性与必要性说明

必要性

假设$x^{\ast }$和$u^{\ast },v^{\ast }$分别是原问题和对偶问题的最优解，且原问题和对偶问题的对偶间隙为0（即强对偶）。那么：
$$\begin{array}{rl}f(x^{\ast })& =g(u^{\ast },v^{\ast })\\ & =\underset{x}{\min }f(x)+\sum _{i=1}^m{u}_i^{\ast }{h}_i(x)+\sum _{j=1}^r{v}_j^{\ast }{l}_j(x)\\ & \le f(x^{\ast })+\sum _{i=1}^m{u}_i^{\ast }{h}_i(x^{\ast })+\sum _{j=1}^r{v}_j^{\ast }{l}_j(x^{\ast })\\ & \le f(x^{\ast })\end{array}$$

即所有不等式都可以取等号。因此，我们可以得到：

• 点$x^{\ast }$最小化$L(x,u^{\ast },v^{\ast })$，那么$L(x,u^{\ast },v^{\ast })$在$x=x^{\ast }$处的次微分一定包含0——即稳定性条件。
• ${\sum }_{i=1}^m{u}_i^{\ast }{h}_i(x^{\ast })=0$——即互补松弛性

必要性：如果$x^{\ast }$和$u^{\ast },v^{\ast }$分别是原问题与对偶问题的解，且对偶间隙为0，那么$x^{\ast },u^{\ast },v^{\ast }$满足KKT条件。

充分性

如果存在$x^{\ast },u^{\ast },v^{\ast }$满足KKT条件，那么
$$\begin{array}{rl}g(u^{\ast },v^{\ast })& =f(x^{\ast })+\sum _{i=1}^m{u}_i^{\ast }{h}_i(x^{\ast })+\sum _{j=1}^r{v}_j^{\ast }{l}_j(x^{\ast })\\ & =f(x^{\ast })\end{array}$$

因此，对偶间隙为0，所以$x^{\ast }$和$u^{\ast },v^{\ast }$分别是原问题与对偶问题的解。
充分性：如果$x^{\ast },u^{\ast },v^{\ast }$满足KKT条件，那么$x^{\ast }$和$u^{\ast },v^{\ast }$分别是原问题与对偶问题的解

总结

综上所述，KKT条件等价于对偶间隙为0：

• 总是充分的
• 在强对偶条件下是必要的

那么我们可以得到：如果一个问题有强对偶性，那么$x^{\ast },u^{\ast },v^{\ast }$满足KKT条件与$x^{\ast }$和$u^{\ast },v^{\ast }$分别是原问题与对偶问题的解是等价的。
可以看出，对于无约束优化问题，KKT条件就是次梯度最优化条件。对于一般性凸优化问题，KKT条件是次梯度最优化条件的推广。

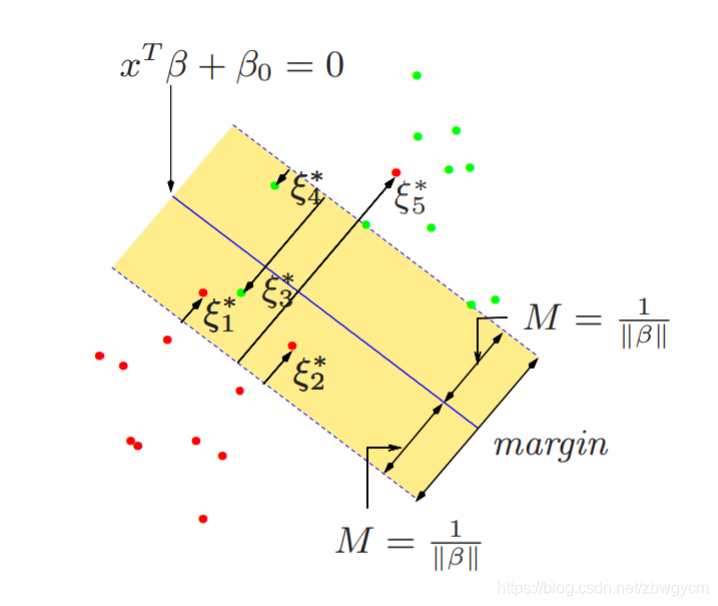
例子：支持向量机（SVM）
给定 y ∈ { − 1 , 1 } n y\in \{-1,1\}^n y∈{−1,1}n，$X\in R^{n\times p}$有行向量$x_1,...,x_n$，则支持向量机(SVM)定义为：
$$\begin{array}{rl}\underset{\beta ,{\beta }_0,\xi }{\min }& \frac{1}{2}\Vert \beta {\Vert }_2^2+C\sum _{i=1}^n{\xi }_i\\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& {\xi }_i\ge 0,i=1,...,n\\ & y_i(x_i^T\beta +{\beta }_0)\ge 1-{\xi }_i,i=1,...,n\end{array}$$

引入对偶变量$v,w\ge 0$。KKT稳定性条件为：
$$0=\sum _{i=1}^n{w}_i{y}_i,\beta =\sum _{i=1}^n{w}_i{y}_i{x}_i,w=C1-v$$

互补松弛性：
$$v_i{\xi }_i=0,w_i(1-{\xi }_i-y_i(x_i^T\beta +{\beta }_0))=0,i=1,...,n$$

因此，在最优点处我们有$\beta ={\sum }_{i=1}^n{w}_i{y}_i{x}_i$，且仅当$y_i(x_i^T\beta +{\beta }_0)=1-{\xi }_i$，$w_i$是非零的，这些点$i$被叫做支持点（support points）

• 对于支持点$i$，如果${\xi }_i=0$，则$x_i$位于分割边界上，且$w_i\in (0,C]$；
• 对于支持点$i$，如果${\xi }_i\ne 0$，则$x_i$位于分割边界的错误一边，且$w_i=C$；
  

有约束形式与拉格朗日形式

在统计和机器学习中，我们常常把一个优化问题在其有约束形式（constrained form），即
$$\underset{x}{\min }f(x)\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}h(x)\le t$$

和拉格朗日形式（Lagrange form），即
$$\underset{x}{\min }f(x)+\lambda \cdot h(x)$$

之间进行互换，并认为这两种形式是等价的。由上面分析可知，假如$f,h$都是凸函数，这种等价在$h(x)<t$时是成立的。

Conclusion

对偶的一个关键性质是，在强对偶条件下，KKT条件是最优解的充要条件，即原问题的解可以通过其对偶问题得到。由于对偶问题一定是凸优化问题，这在对偶问题比原问题更简单时非常有用。