目录
一、单调递增的数字
贪心策略:
对于这道题,相邻数字相等,也表示是递增的。
解题代码:
class Solution
{
public:
int monotoneIncreasingDigits(int n)
{
string s = to_string(n);
int i = 0;
while(i+1 < s.size() && s[i] <= s[i+1])
i++;
if(i+1 == s.size())
return n;
while(i >= 1 && s[i] == s[i-1])
i--;
s[i]--;
i++;
while(i < s.size())
s[i++] = '9';
return stoi(s);
}
};二、坏了的计算器
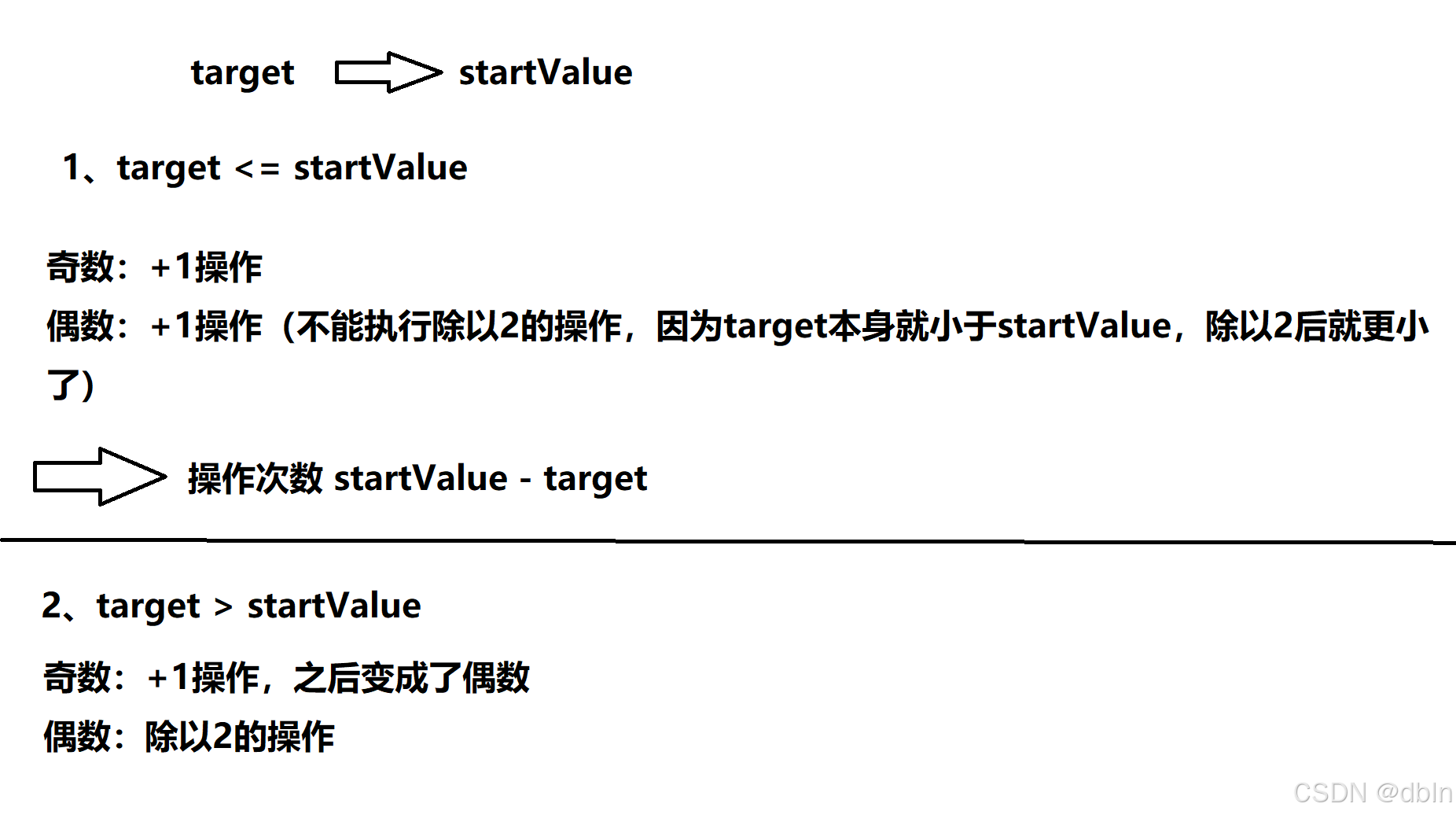
贪心策略:
题目要求找从startValue到target的最小操作数。其实这道题找从target到startValue的最小操作数更容易一些。相应的,操作方式就变成了,除以2和加1。
注:对于原来的操作,乘以2和减1来说,因为操作的是整数,所以是不会出现的小数的。因此,对于除以2和加1的操作来说,除以2的操作就不能出现小数。也就是说,只有偶数才能执行除以2的操作,奇数只能执行加1的操作。
解题代码:
class Solution
{
public:
int brokenCalc(int startValue, int target)
{
int ret = 0;
while(target > startValue)
{
if(target % 2)
target++;
else
target /= 2;
ret++;
}
return ret + startValue - target;
}
};三、合并区间
贪心策略:
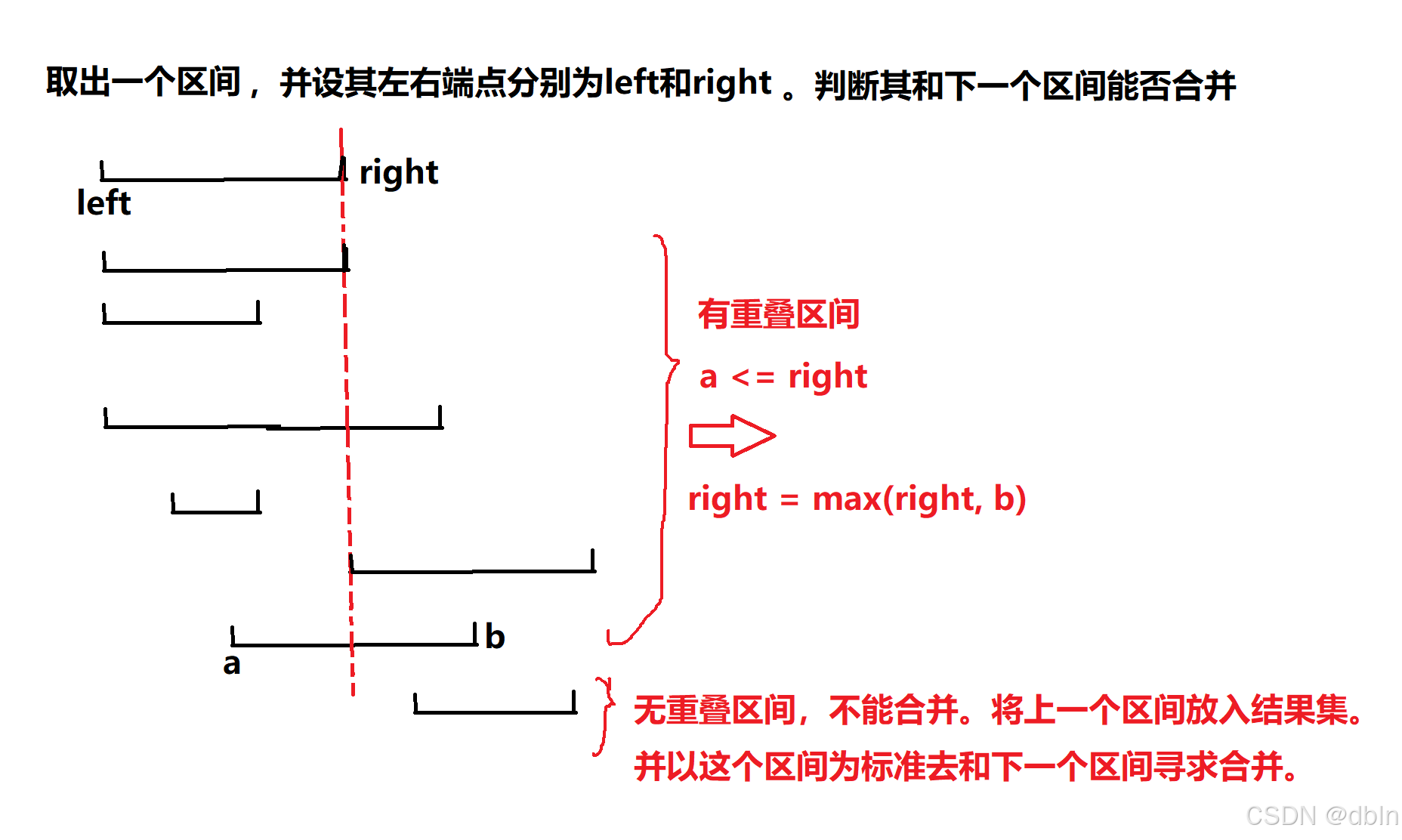
第一步:排序,默认按左端点排序。排序后,我们能够保证能够合并的区间一定是连续的,挨在一起的。
第二步:从左到右判断,合并区间。
解题代码:
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end());
vector<vector<int>> ret;
int left = intervals[0][0], right = intervals[0][1];
int n = intervals.size();
for(int i = 1; i < n; i++)
{
int a = intervals[i][0], b = intervals[i][1];
if(a <= right)
right = max(right, b);
else
{
ret.push_back({left, right});
left = a;
right = b;
}
}
ret.push_back({left, right});
return ret;
}
};
四、无重叠区间
贪心策略:
首先进行排序,默认按左端点排序。排序后,我们能够保证有重叠部分的区间一定是连续的,是挨在一起的。
题目要求移除最少的区间,使这些区间没有重叠。换句话说,就是要保留尽量多的区间,使这些区间没有重叠部分。 只要找到能够保留下来多少区间,就能够得出需要移除多少区间了。
解题代码:
class Solution
{
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end());
int left = intervals[0][0], right = intervals[0][1];
int count = 0;
for(int i = 1; i < intervals.size(); i++)
{
int a = intervals[i][0], b = intervals[i][1];
if(a < right)
right = min(right, b);
else
{
count++;
left = a;
right = b;
}
}
count++;
return intervals.size()-count;
}
};五、用最少数量的箭引爆气球
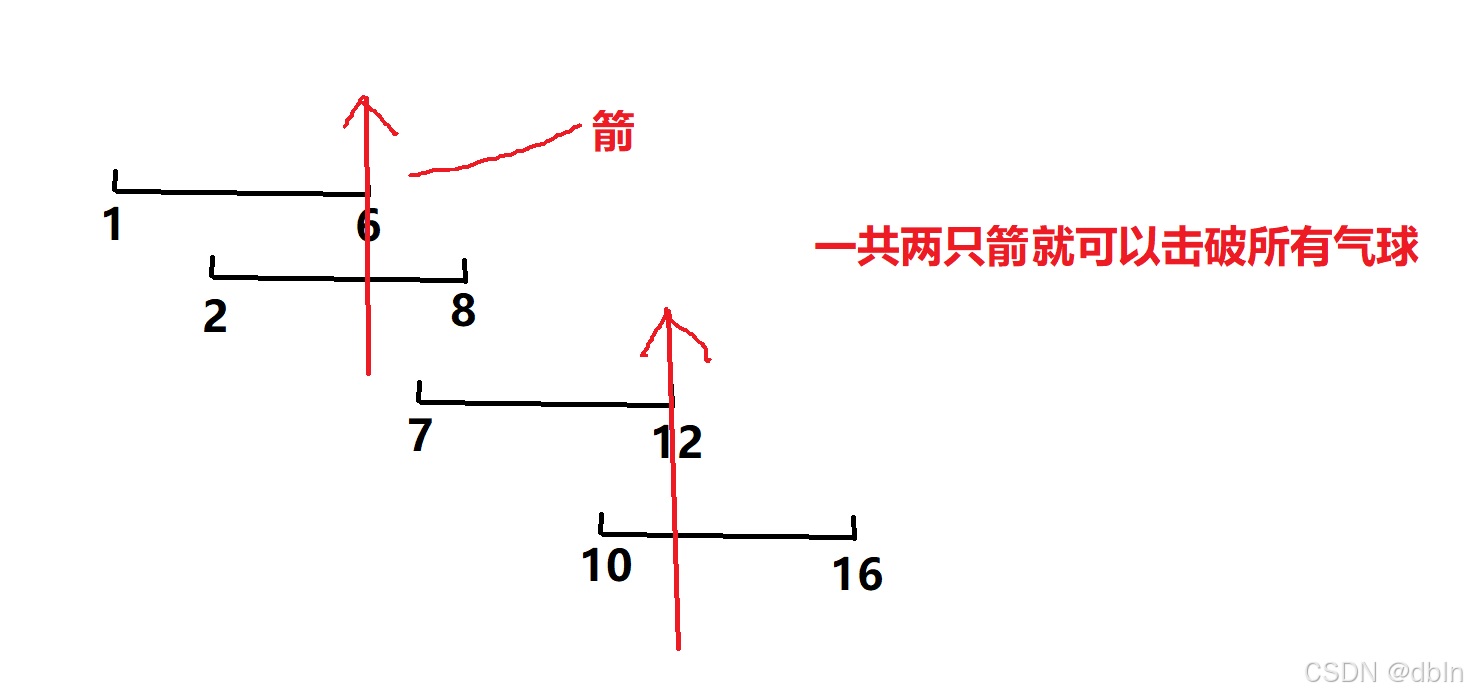
根据示例一来分析一下题目:
题目要求使用数量最少的弓箭去引爆气球,那么一只箭就应该引爆尽量多的气球。所以,我们需要将两两互相重叠的所有区间都拿出来,用一支箭将其引爆。
贪心策略:
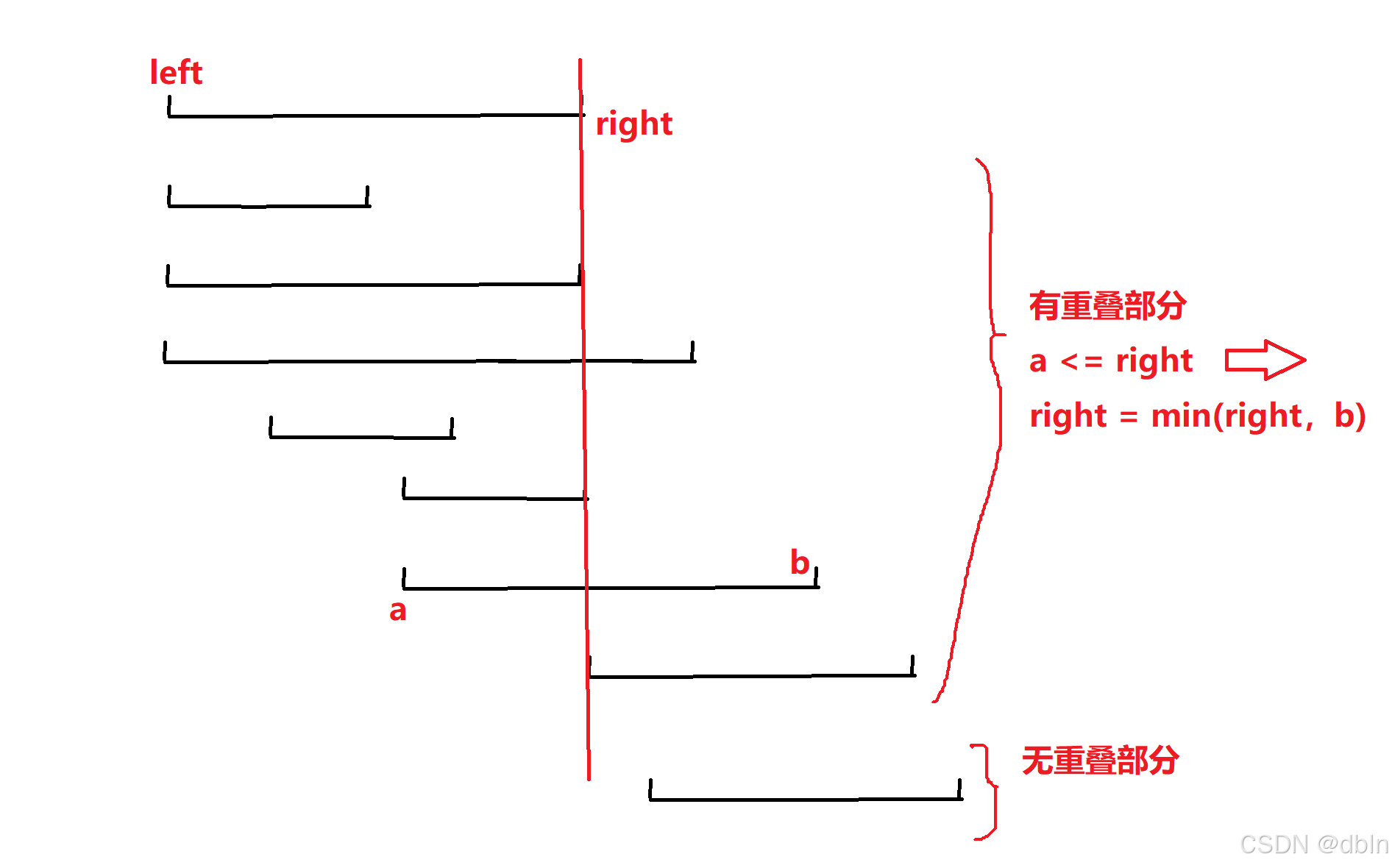
根据题目,我们可以知道:在几个区间中,如果这些区间两两相互重叠,那么说明它们有公共部分,那么我们就可以用一支箭将他们全部引爆。再进一步思索,这些区间有公共部分,那就说明它们的交集是不为空的。
所以说,这道题就是找出所有互相重叠的区间,也就是求区间的交集。
首先进行排序,默认按左端点排序。排序后,我们能够保证有重叠部分的区间一定是连续的,是挨在一起的。
然后,从左到右判断,求区间的交集。
解题代码:
class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
sort(points.begin(), points.end());
int right = points[0][1];
int n = points.size(), count = 1;
for(int i = 1; i < n; i++)
{
int a = points[i][0], b = points[i][1];
if(a <= right)
right = min(right, b);
else
count++, right = b;
}
return count;
}
};