[SVM系列之三]间隔与支持向量

问题引入

（1）首先回答一个问题，下面哪一条线最优？

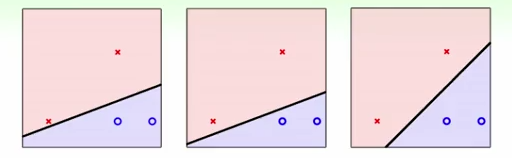
显然，最右侧的分割最优。

（2）为什么最优呢？

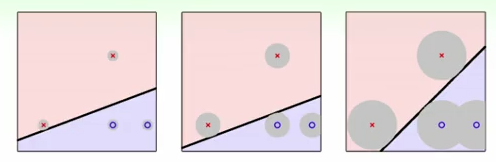
由上图可以看出，它的容错性更好，它使得所有样本与分割超平面的距离尽可能远，或者可以说最差的样本（离分割超平面最近的样本）与分割超平面的距离要尽可能远。因此，SVM的目的就是从无数多个分割超平面中，找到这样最好的分割超平面。

通常情况下，一个点距离超平面的远近可以表示为分类预测的准确程度。

在超平面 $w \cdot x+b = 0$ 确定的情况下， $|w \cdot x + b|$ 能够相对的表示点 $x$ 到超平面的远近，而 $w \cdot x + b$ 的符号与类标记 $y$ 的符号是否一致表示分类是否正确。所以，可以用量 $y \cdot (w \cdot x + b)$ 的正负性来判定或表示分类的正确性和确信度，并且 $y \cdot (w \cdot x + b)$ 的值越大，分类结果的确信度越大。反之亦然。

由此引入了定义样本到分类间隔距离的函数间隔（Functional Margin）的概念。

函数间隔

样本点 $(x_i, y_i)$ 到超平面 $(w,b)$ 之间的函数间隔定义为：

γ^= y \cdot (w T x + b) = y f (x) (2.1)

$\hat{\gamma}= y \cdot (w^T x + b) = yf(x) \tag{2.1}$

然后，我们定义超平面 $(w, b)$ 关于训练数据集 $T$ 的函数间隔为超平面 $(w, b)$ 关于 $T$ 中所有样本点 $(x_i, y_i)$ 的函数间隔最小值，其中 $x$ 是特征， $y$ 是结果标签， $i$ 表示第 $i$ 个样本，有：

γ^= m i n (γ^i), i = 1, 2, \dots, n (2.2)

$\hat{\gamma}=min(\hat{\gamma}_i), i=1,2,\ldots,n \tag{2.2}$

我们很容易地可以发现这种定义方式的问题，对于分类超平面 $w \cdot x+b = 0$ 来说，如果成比例地改变 $w$ 和 $b$ ，比如改为 $2w$ 和 $2b$ ，则此时超平面并未改变，但函数间隔值却变为了原来的4倍。

其实，我们可以对法向量 $w$ 加些约束条件，如 $||w||=1$ ，使函数间隔固定，其表面上也就看起来规范化，如此，我们很快又将引出真正定义点到超平面的距离——几何间隔（Geometric Margin）的概念。

几何间隔

几何间隔，顾名思义，此间隔可以反映出空间上的几何关系。

我们首先来看一个例子，见下图。

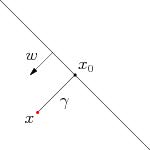
对于一个点 $x$ ，令其垂直投影到超平面上的对应点为 $x_0$ ，由于 $w$ 是垂直于超平面的一个向量， $\gamma$ 为样本 $x$ 到分类间隔的距离，我们有：

\begin{matrix} (2.3) & x = x_{0} + γ \frac{w}{| | w | |} \end{matrix}

$x=x_0+\gamma \frac{w}{||w||} \tag{2.3}$

又由于 $x_0$ 是超平面上的点，满足 $f(x_0) = 0$ ，代入式 $(2.3)$ ，消去 $x_0$ ，得到：

γ = w T x + b | | w | | = f ( x ) | | w | | (2.4)

$\gamma = \frac{w^Tx+b}{||w||} = \frac{f(x)}{||w||} \tag{2.4}$

注：这里的 $\gamma$ 是带符号的，我们需要的只是它的绝对值，因此类似地，也乘上对应的类别 $y$ 即可，因此实际上我们定义几何间隔为：

\begin{matrix} (2.5) & \tilde{γ} = y γ = \frac{\tilde{γ}}{| | w | |} \end{matrix}

$\tilde{\gamma}=y\gamma=\frac{\tilde{\gamma}}{||w||} \tag{2.5}$

加深理解
1. 函数间隔 $y \cdot (w^T x + b) = yf(x)$ 实际上就是 $|f(x)|$ ，只是人为定义的一个间隔度量；
2. 几何间隔 $\frac{f(x)}{||w||}$ 才是空间上的点到超平面距离，具有实际物理意义。比如：
若以二维空间为例，点坐标设为 $(x_0, y_0)$ ，直线（若多维空间则是超平面）设为 $Ax+By+C=0$ ，则点到平面的距离为：

$d = ∣ ∣ ∣ A x 0 + B y 0 + C A 2 + B 2 - - - - - - - \sqrt ∣ ∣ ∣$ $d=\left| \frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}} \right|$

最大间隔分类器

对函数间隔和几何间隔定义的观察可以看出，它们相差一个 $||w||$ 缩放因子，按照 问题引入 部分的分析，对一个数据点进行分类，当它的间隔越大的时候，分类正确的把握越大。对于一个包含 $n$ 个点的数据集，我们可以很自然地定义它的间隔为所有这 $n$ 个点的间隔中最小的那个。于是，为了使得分类结果的鲁棒性尽量大，对未知样本的泛化能力最强，我们希望所选择的超平面能够最大化这个间隔值。

因此，最大间隔分类器（Maximum Margin Classifier）定义为：

m a x (γ ~) (2.6)

$max(\tilde{\gamma}) \tag{2.6}$

根据 间隔为最小 的定义，我们有：

γ^= m i n (γ^i), i = 1, 2, \dots, n (2.7)

$\hat{\gamma}=min(\hat{\gamma}_i), i=1,2,\ldots,n \tag{2.7}$

其中， $\hat{\gamma}=\tilde{\gamma}||w||$ （即 $\tilde{\gamma}= \frac{\hat{\gamma}}{||w||}$ ）。

由于 希望所选择的超平面能够最大化这个间隔值 ，故 SVM 可以表述为求解下列优化问题，即式子 $(2.7)$ 可以表示为：

m a x (γ ^ | | w | |) s . t . y i \cdot (w T x i + b | | w | |) \geq γ ^ | | w | | (2.8) (2.9)

$\begin{align} & max(\frac{\hat{\gamma}}{||w||}) \tag{2.8}\\ & s.t. \quad y_i \cdot \left( \frac{w^Tx_i+b}{||w||} \right) \geq \frac{\hat{\gamma}}{||w||} \tag{2.9} \end{align}$

为了便于优化推导，我们可以令 $\hat{\gamma}=1$ ，式 $(2.8)$ 和 $(2.9)$ 可以转化为：

m a x (1 | | w | |) s . t . y i \cdot (w T x i + b) \geq 1 (2.10) (2.11)

$\begin{align} & max(\frac{1}{||w||}) \tag{2.10}\\ & s.t. \quad y_i \cdot ( w^Tx_i+b ) \geq 1 \tag{2.11} \end{align}$

对这个问题的求解，我们可以找到一个间隔最大的分类器中间的红色线条是最优超平面，另外两条线到红线的距离都是等于 $\tilde{\gamma}$ 的，见下图：

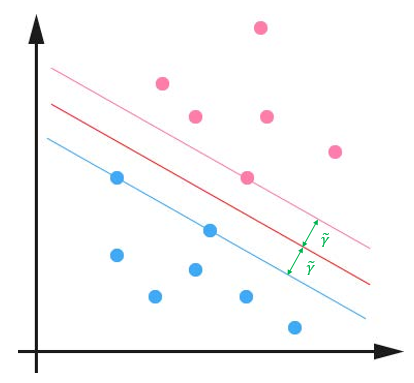
支持向量机通过使用最大分类间隔来设计决策最优分类超平面，而为何是最大间隔，却不是最小间隔呢？

因为最大间隔能获得最大稳定性与区分的确信度，从而得到良好的推广能力（超平面之间的距离越大，分离器的推广能力越好，也就是预测精度越高，不过对于训练数据的误差不一定是最小的）。

支持向量

在下图中，我们可以看到两个支撑着中间的间隙的超平面（粉色和蓝色直线），它们到中间的纯红线（分类超平面）的距离相等，即我们所能得到的最大的几何间隔 $\tilde{\gamma}$ ，而这些“支撑”的点（图中绿色圈出的点）便叫做支持向量（Support Vector）。

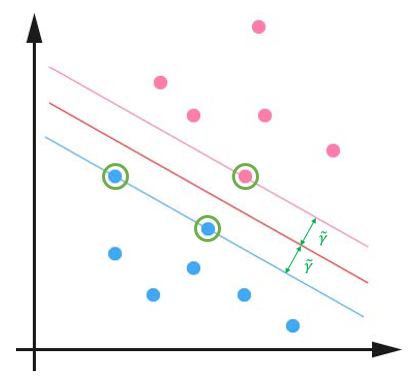
显然，根据式 $(2.11)$ ，这些支持向量刚好在边界上，因此满足 $y_i \cdot ( w^Tx_i+b ) = 1$ 。而对于所有不是支持向量的点，则显然有 $y_i \cdot ( w^Tx_i+b ) > 1$ 。

后记：到本节为止，你可以算了解了SVM，若你只关心怎么用SVM，到此为止已经足够了。在后续教程中，我们会更加深入探讨 SVM 的原理，对自己要求比较高的童鞋，让我们继续吧。

参考文献

[1] 支持向量机通俗导论（理解SVM的三层境界) - July
[2] 支持向量机中的函数距离和几何距离怎么理解？ - Jason Gu的回答 - 知乎
[3] 周志华 - 《机器学习》
[4] 李航 - 《统计学习方法》

更多机器学习干货、最新论文解读、AI资讯热点等欢迎关注“AI学院(FAICULTY)”，内容持续更新中……
欢迎加入faiculty机器学习交流qq群：451429116(点此进群)
版权声明：本文不可任意转载，转载请联系作者。