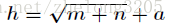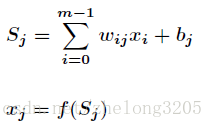BP （Back Propagation）神经网络简介 ：

先介绍一下神经元，在生物神经网络中，每个神经元与其它神经元相连，当一个神经元“兴奋”时，就会通过穿出神经向其它神经元发送化学物质，其它神经元会通过穿人神经接受信息然后再传递至神经中枢处理信息。现在机器学习中的神经网络就是基于生物学中的神经元模型的。一个一个的神经元与其它神经元相互连接构成所谓的神经网络。

BP 神经网络分为两个过程
1. 工作信号正向传递子过程
2. 误差信号逆向传递过程

在一般的BP神经网络中，单个样本有m个输入和n个输出，在输入层和输出层之间还有若干个隐藏层，实际上 1989年时就已经有人证明了一个万能逼近定理 ：
在任何闭区间的连续函数都可以用一个隐藏层的BP神经网络进行任意精度的逼近。
所以说一个三层的神经网络就可以实现一个任意从m维到n维的一个映射。这三层分别是
输入层、隐藏层、输出层 如图所示 ：

关于隐藏层的选择 ：
在BP神经网路中，输入层和输出层的节点数目都是固定的，关键的就是在于隐藏层数目的选择，隐藏层数目的选择决定了神经网络工作的效果

一般而言，有一个关于隐藏层数目的经验公式

其中 h 为隐藏层节点数目，m为输入层节点数目，n为输出层节点数目 a 为 1-10 之间的调节常数。一般而言如果数据多的话我们可以设a稍微大一点，而数据不是太多的时候就设置的小一点防止过拟合。

正向传递子过程 ：
设节点 i 与 节点 j 之间的权值 为 wij，节点 j 的阀值为 bj，每个节点的输出值为 xj，具体的计算方法如下

其中 f 为激活函数 ，一般选择sigmoid函数或者 线性函数正向传播中输入层没有阀值

BP神经网络的关键之处就在于