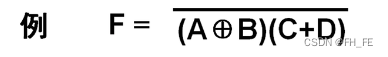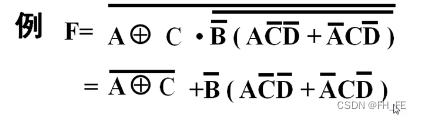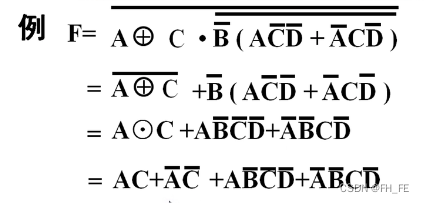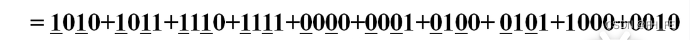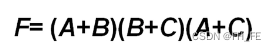文章目录
数字逻辑设计(2)
1. 多变量卡诺图
1.1 多变量卡诺图的概念
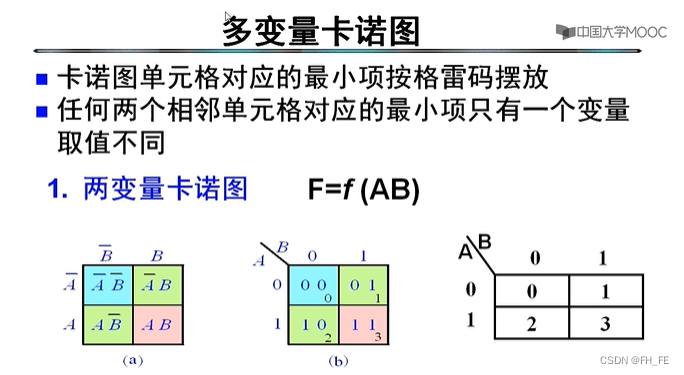
1. 两变量卡诺图
利用格雷码,使用坐标的读取方式,将格雷码组成后以二进制转为十进制读取
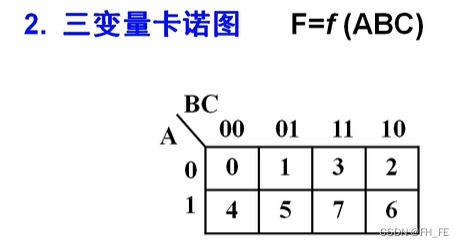
2. 三变量卡诺图
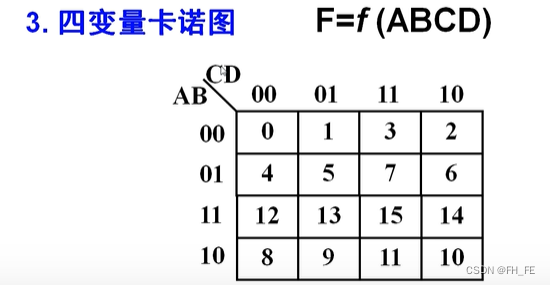
3. 四变量卡诺图
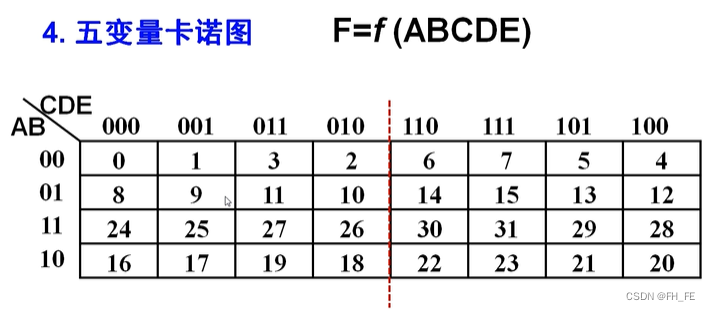
4. 五变量卡诺图
1.2 如何填写多变量卡诺图
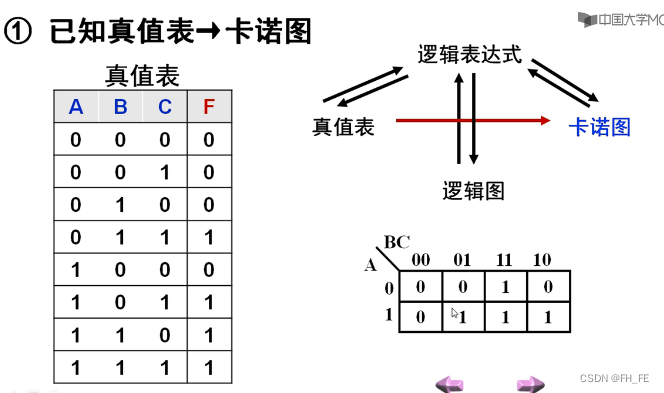
1.2.1 真值表 -》卡诺图
根据真值表中的结果,对应到卡诺图表格中填写对应的0,1值
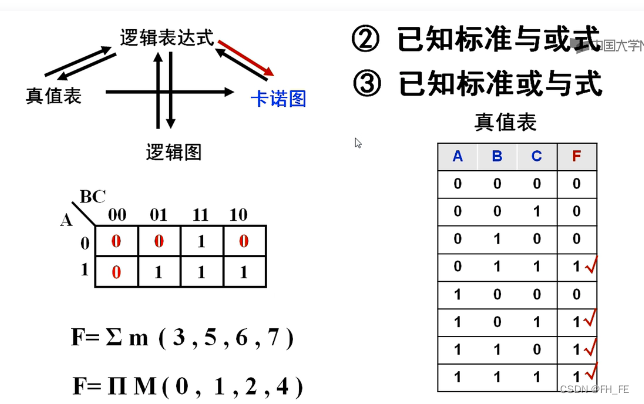
1.2.2 标准与或式 -》卡诺图
标准与或式
F
=
∑
m
(
3
,
5
,
6
,
7
)
F=\sum{m(3, 5, 6, 7)}
F=∑m(3,5,6,7)
即编号3,5,6,7对应的真值为1,填写真值表中,再对应填写到卡诺图中
标准或与式
F
=
∏
m
(
0
,
1
,
2
,
4
)
F=\prod{m(0, 1, 2, 4)}
F=∏m(0,1,2,4)
即编号0,1,2,4对应的真值为0,填写在真值表中,再对应到卡诺图中
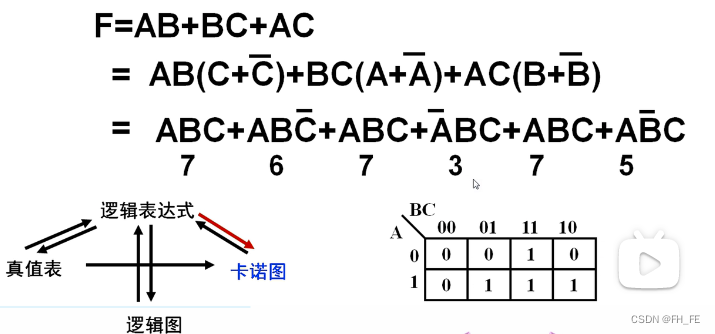
将与或式逻辑表达式展开成完整形式,将对应的编号在卡诺图中填写为1
1.2.3 例题
F
=
(
A
⨁
B
)
(
C
+
D
)
‾
F=\overline{(A \bigoplus B)(C + D)}
F=(A⨁B)(C+D)
F
=
(
A
B
‾
+
A
B
)
‾
(
C
+
D
)
‾
F=\overline{\overline{(\overline{AB} + AB)}(C + D)}
F=(AB+AB)(C+D)
F
=
A
‾
F=\overline{A}
F=A
B
‾
+
A
B
+
C
‾
\overline{B} + AB + \overline{C}
B+AB+C
D
‾
\overline{D}
D
补出最小项
A
‾
\overline{A}
A
B
‾
\overline{B}
B = 0000 + 0001 + 0010 + 0011
0 1 2 3
A
A
A
B
B
B = 1100 + 1101 + 1110 + 1111
12 13 14 15
C
‾
\overline{C}
C
D
‾
\overline{D}
D = 0000 + 0100 + 1000 + 1100
0 4 8 12
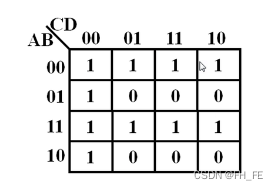
填写卡诺图得
首先求出逻辑表达式
再补全最小项
最后根据编码号补全卡诺图
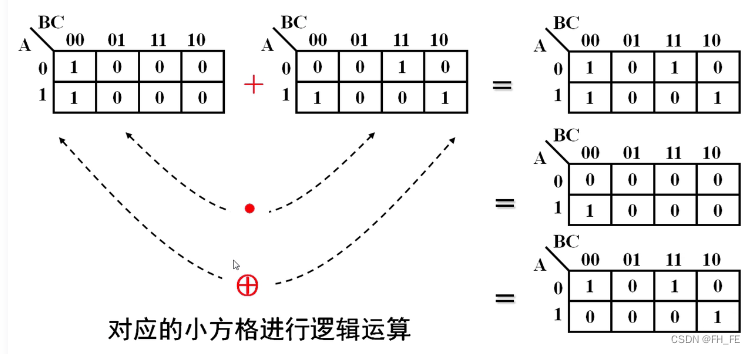
1.2.4 基于卡诺图得逻辑运算
卡诺图之间的逻辑运算是对应小方格之间进行逻辑运算:
或、与、异或、同或等
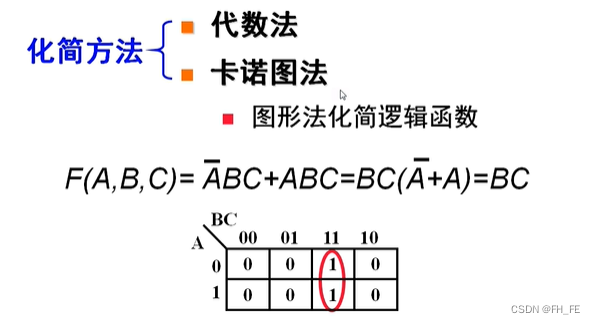
2. 卡诺图化简法
B
C
BC
BC全为1,在卡诺图中表现为
B
C
BC
BC 即11纵行全是1
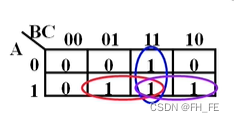
2.1 从卡诺图中读取最简与或式(AND-OR)
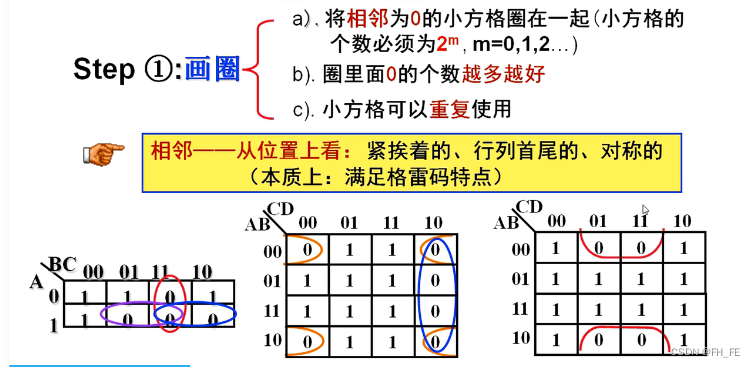
step1 画圈
1. 紧挨着的2. 行列首尾相接的
3. 对称的
满足格雷码的特点,相邻两项只有一位不同
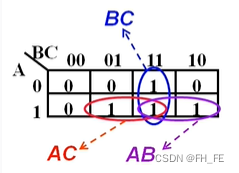
三个圈
011 & 111
101 & 111
110 & 111
一个圈
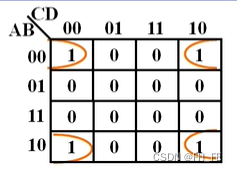
0000 & 0010 & 1010 & 1000
一个圈
0001 & 0011 & 1011 & 1001
step2. 求出每个圈代表的项(每个圈代表一个与项)
观察每个圈左边和上边(类似于坐标读取方法),0和1同时出现的项和为1,在项的表达式中消除,只出现0或1的项取原变量或者反变量在项中保留
蓝色的圈
左边有
A
A
A:0,1 同时出现消去
A
A
A
上边有
B
C
BC
BC:11 没有在逻辑上消去,得到
B
C
BC
BC
综上,得到了项表达式
B
C
BC
BC
红色的圈
左边有
A
A
A: 1 得到项中的一部分,即
A
A
A
上边有
B
C
BC
BC: 01和11将B消去,的到项的另一部分,即
C
C
C
综上,得到了表达式
A
C
AC
AC
紫色的圈
同上,消去
C
C
C, 得到项
A
B
AB
AB
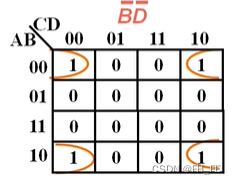
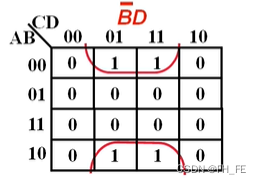
从圈的位置
读取左侧值
00 & 10 消去B
读取上侧值
00 & 10 消去C
综上,得到表达式
B
‾
\overline{B}
B
D
‾
\overline{D}
D
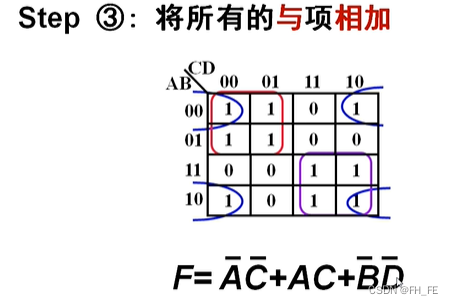
step3. 将所有的与项相加
得到最简逻辑表达式
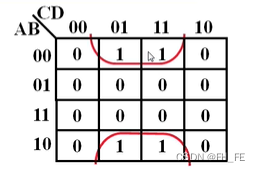
1. 画圈
相邻对称2个圈
行列首尾1个圈
2. 求出每个圈代表的项
红色:
A
‾
\overline{A}
A
C
‾
\overline{C}
C
紫色:
A
A
A
C
C
C
蓝色:
B
‾
\overline{B}
B
D
‾
\overline{D}
D
3. 将所有与项相加
F = F= F= A ‾ \overline{A} A C ‾ \overline{C} C + A A A C C C + B ‾ \overline{B} B D ‾ \overline{D} D
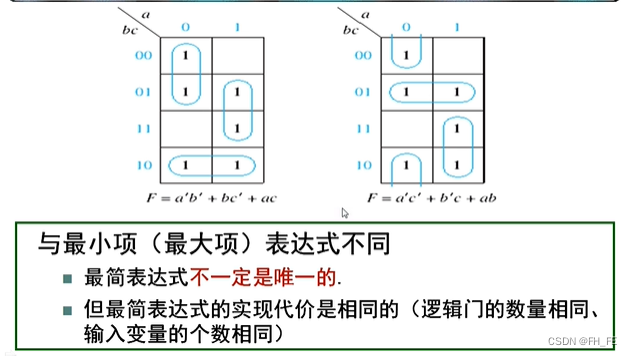
由上图画圈的方式不同可知最简表达式不一定唯一,但是同一个逻辑表达式的最简表达式的实现代价式相同的
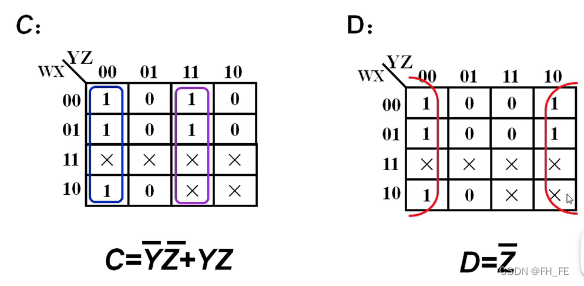
2.2 读取最简或与式(OR-AND)
step1. 画圈
与与或式类似,区别是画圈的目标是0
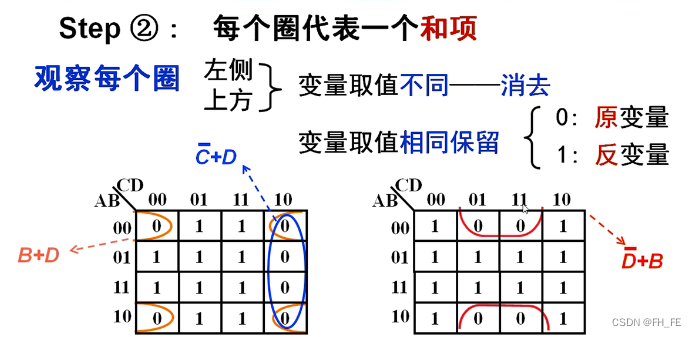
step2. 每个圈代表一个和项
注意:在和项中0代表原变量
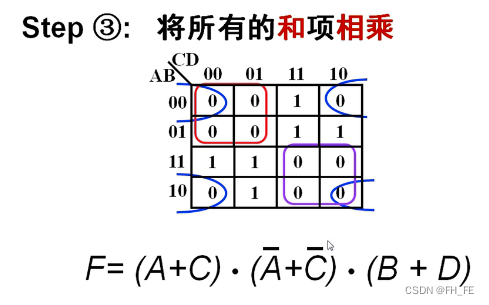
step3. 将所有和项相乘
得到最简或与式
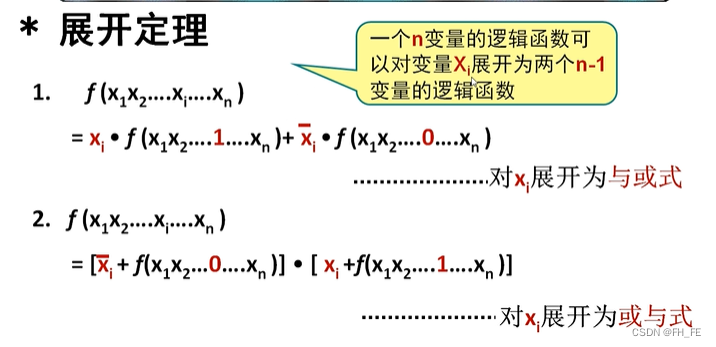
2.3 读取最简与或非式(AND-OR-NOT)
方法一
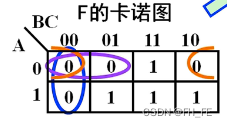
step1. 读 F ‾ \overline{F} F的与或式
在F的卡诺图中圈0
step2. 对 F ‾ \overline{F} F求反
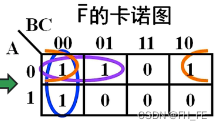
方法二
在 F ‾ \overline{F} F的卡诺图中圈1
俺觉得方法二简单些
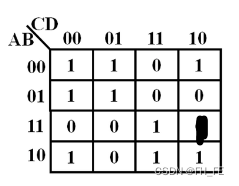
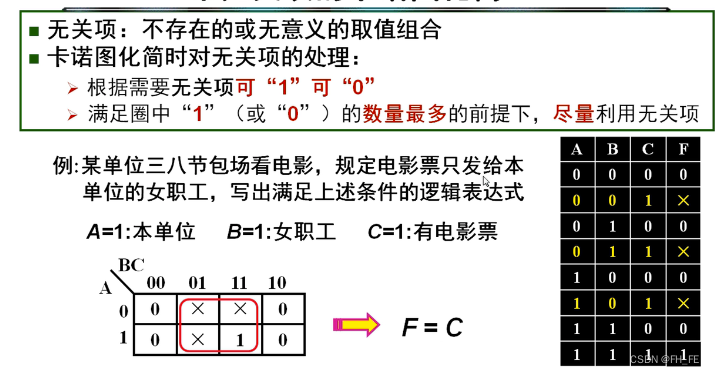
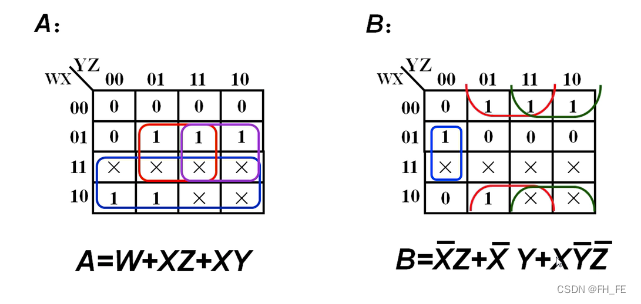
2.4 带有无关项的卡诺图化简
2.4.1 求解方法
在此图中,两种画圈方法:
方法一:求与或式
卡诺图中只有一个1,观察知将无关项视为1时更好画圈,得到一个圈,最终化简结果为
F
=
C
F=C
F=C
方法二:求或与式
卡诺图中此时圈0,得到一个圈,中间的无关项利用不上, 那就不利用了,即视为1即可,否则强行利用反而麻烦。
得到一个圈,最终化简结果为
F
=
C
F=C
F=C
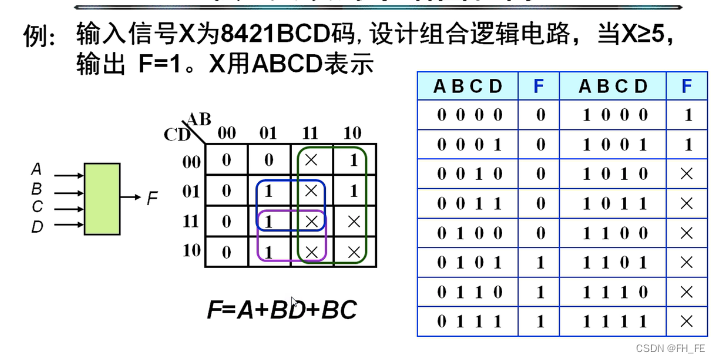
2.4.2 例题
例1
对于8421BCD码,有效范围是0~9,超出这个范围的是无关项
求其与或式时,先对1画圈,包含相邻1的同时,利用更多的无关项,得到三个圈
最终逻辑表达式为
F
=
A
+
B
D
+
B
C
F=A+BD+BC
F=A+BD+BC
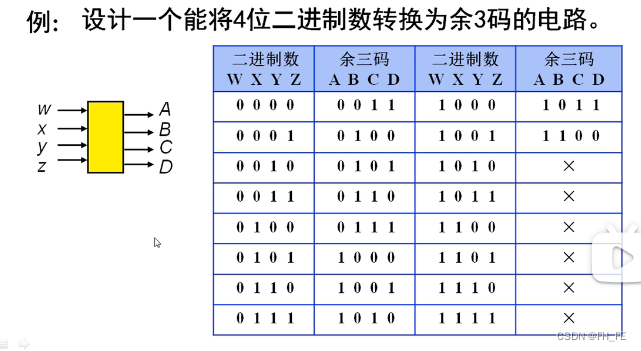
例2
二进制码+3为余三码
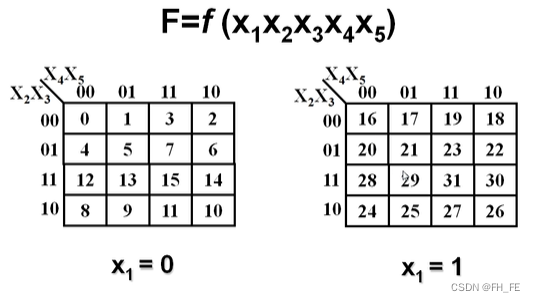
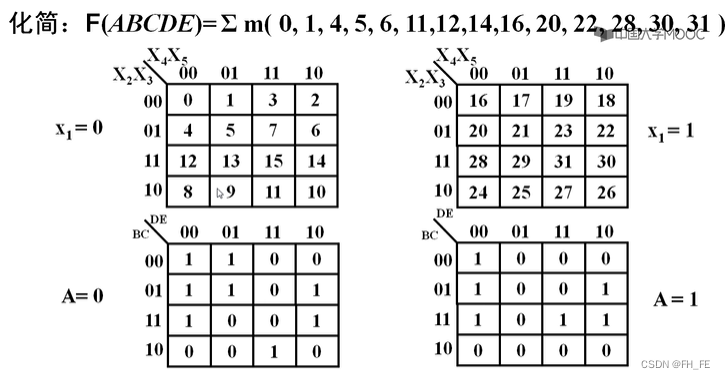
2.5 更多变量的卡诺图化简
左边为
x
1
=
0
x1=0
x1=0时,编号从0~15
右边为
x
1
=
1
x1=1
x1=1时,编号从16~31