题目来源
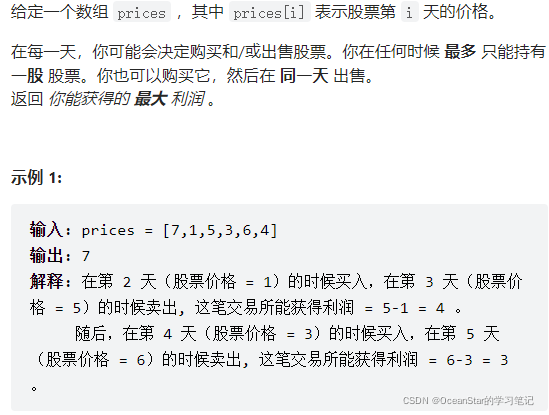
题目描述
题目解析
思路一
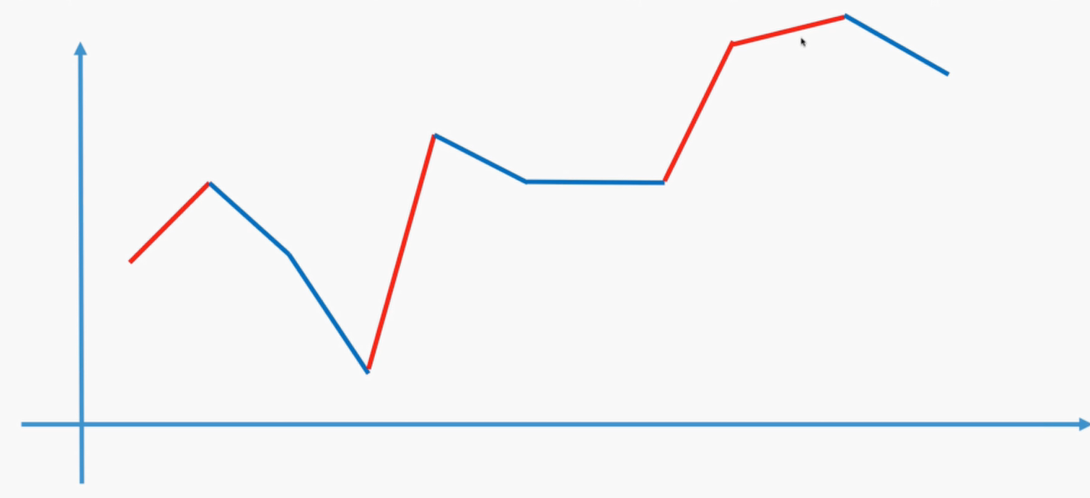
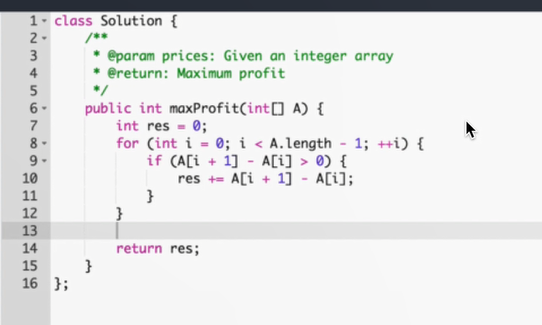
- 买卖任意多次,如果要得到最大利润,就是要把所有上升的地方都买到,下降的时卖出
- 贪心策略:如果今天的价格比明天的低,就今天买、明天卖(只收集正利润)
- 局部最优:收集每天的正利润
- 全局最优:求得最大利润。
- 局部最优可以推出全局最优,找不出反例,试一试贪心!
- 正确性证明:如果最优策略第10天买,第15天卖,我们可以把它分解为5天,结果不会变差
思路二
本题的由来有两种思想, 可以看成将k固定成+∞的情况, 直接将dp数组的第二个维度去掉即可, 就是最终答案.
也可以看成是由k=1的情况变化而来, 这里唯一不同的地方就是:
- 因为可以进行多次买卖, 所以在买入股票的时候, 之前可能会有其他利润.
- 唯一需要更改的地方就是: 第i天买入股票, 所得现金就是昨天不持有股票的所得现金减去 今天的股票价格no[i-1]-prices[i].
因为本题的动态规划方法和[121. 买卖股票的最佳时机]只有一处不同, 其他的思路和代码是一模一样。唯一的不同就是推导have[i]的第二种情况的时候:第i天买入股票的情况是不同的。121题中股票全程只能买卖一次,所以如果买入股票, 那么第i天持有股票即have[i]一定就是 -prices[i], 而本题中, 因为一只股票可以买卖多次, 所以当第i天买入股票的时候, 所持有的现金可能有之前买卖过的利润, 所以have[i]=no[i-1]-prices[i]. 这就是两题唯一不同的地方了, 其他地方都是一模一样了!
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if(n == 0){
return 0;
}
std::vector<int> have(n); // 表示第i天持有股票所得最多的现金
std::vector<int> no(n); // 表示第i天不持有股票做的的最多现金
have[0] = -prices[0];
no[0] = 0;
for (int i = 1; i < n; ++i) {
have[i] = std::max(have[i - 1], no[i - 1] - prices[i]);
no[i] = std::max(no[i - 1], have[i - 1] + prices[i]);
}
return no[n - 1];
}
};
类似题目
| 题目 | |
|---|---|
| 算法:股票问题,最多买卖k次 | |
| 121. 买卖股票的最佳时机(k=1时,买卖1次的情况) Best Time to Buy and Sell Stock | |
| 122. 买卖股票的最佳时机 II(k=+∞时,买卖多次)Best Time to Buy and Sell Stock II |