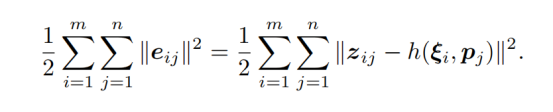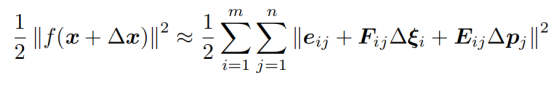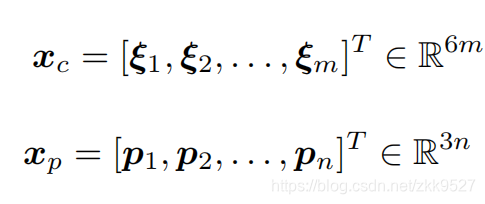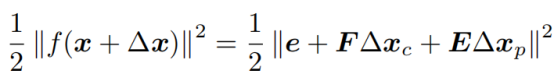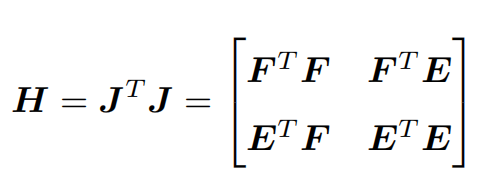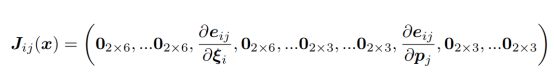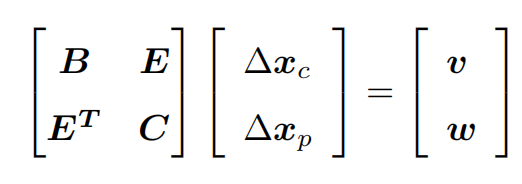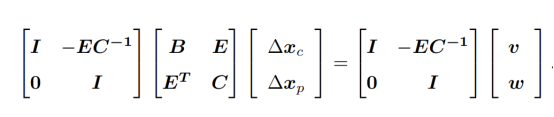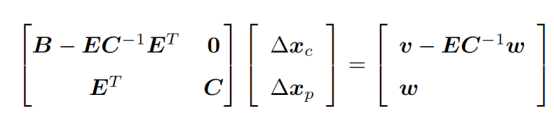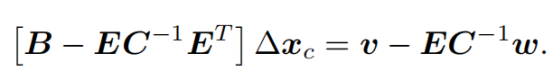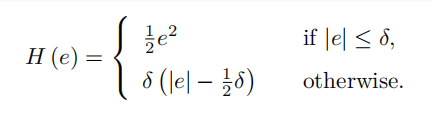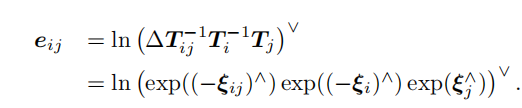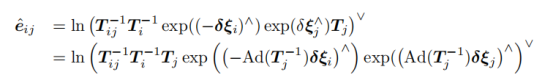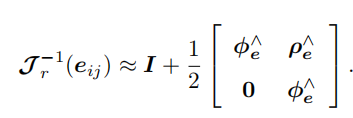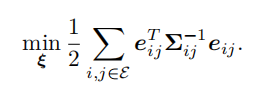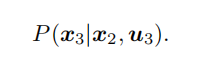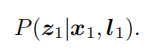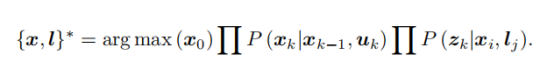上一节内容中我总结了卡尔曼滤波器的推导及其扩展的过程SLAM14讲学习笔记(六)后端(最难一章:卡尔曼滤波器推导、理解以及扩展),我认为那部分内容直接接触是比较难以理解的。但是高博书中也说了,卡尔曼滤波器并不是主流方法,主要还是通过BA或者其他方式来做优化。
SLAM十四讲中,后端分为两节,在我的笔记里,把卡尔曼滤波器单独拿出来做了一个笔记,然后剩下的内容总结在这里,作为第二个后端优化的笔记。在我的slam学习中,第一次只是大致把细节的地方都抠了抠,然后把代码跑通了,然而并没有融会贯通。第二次学习的目的是把理论的部分追根问底然后前后能联系起来,代码的东西第三遍再去深究。因此本文不包括代码内容,只包括公式推导。第三次学习的时候,把后端的代码总结了一下,参见:SLAM14讲学习笔记(十三)ch10 后端1(代码详述)
BA
BA的内容在前面出现了很多次,几乎就是和“非线性优化”划了等号了。Bundle Adjustment翻译过来是“光束调整”,意思是每个特征反射的光束,通过调整它们的空间位置和相机姿态,使它们都汇聚到相机光心,这个过程叫BA。
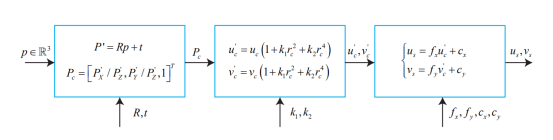
上面这个图描述了从世界坐标系到像素坐标系的变换过程,注意中间把之前一直不考虑的相机畸变过程考虑进来了。
最后通过计算得到的像素坐标与实际拍摄到的像素坐标相减作为误差,构造一个代价函数(我感觉基本就是重投影误差嘛):
重投影误差的那部分内容已经在视觉里程计那里总结过了,但是这章和那章的区别在于,误差项都是针对于单个位姿和路标点的,但是在整体的BA目标函数上,必须把自变量定义成所有待优化的变量。(也就是说,视觉里程计的两章里的BA,主要针对的是讲单个误差项的求导过程,但是这章讲的是所有的误差合并到一起,做一个整体的矩阵进行优化)
先从单个误差项入手,BA跟别的优化的区别在于,别的方法是先求位姿,再求点坐标,BA是把两者全部都放在一起进行优化。因此误差函数的值受两个因素影响:一个是相机姿态,一个是所谓路标点(也就是特征点)。因此可以求误差函数关于二者的偏导数,也就是之前所述的两个偏导数,2*6的那个雅克比矩阵是误差对于扰动的小量位姿的偏导数;2*3的那个雅克比矩阵是误差对于特征点相机坐标系下坐标的偏导数,它再乘以一个3*3的R得到一个2*3的雅克比矩阵就是误差关于特征点世界坐标系下坐标的偏导数,具体内容看 SLAM14讲学习笔记(五)视觉里程计(光流法和直接法)和对于雅克比矩阵的理解
把对相机姿态的偏导数记为F,对路标点的偏导数记为E,得到:
这里的i和j的含义是,因为对于整体的优化过程,不只有一个位姿,也不只有一个特征点。所以把所有的位姿作为一个变量xc,所有的空间点作为一个变量xp:
因此之后修改的小量△x,就是针对这两个“整体的变量”进行的扰动和修正,这样目标函数的增量扰动公式就变成了:
(没有了ij)
回顾非线性优化的知识,最后是通过合起来的雅克比矩阵J和自身的转置乘积(列温伯格马尔夸特方法还要加个λI),来计算代替海塞矩阵H,从而构造H△x=g求解△x。
以高斯牛顿法为例,先把雅克比矩阵分块,变成J=[F,E],然后得到H矩阵的近似:
这个H△x=g的求解我觉得是非常蛋疼的,因为把所有的特征点都列进去了(一张图就几百个特征点,那这个矩阵不得几万乘几万?那这个得是多大的方程组?怎么求解?
因此高博指出了这的H矩阵是有特殊结构的,可以利用特殊结构来加速求解过程。
高博把稀疏结构列到这里:
这个J表示误差对于第i个位姿看到第j个路标点的误差,前面的是对于位姿的,后面的是对于路标点的。
关于这个Jx,可以这么理解,因为之前构造的误差函数,一个点就能得到一个误差了。一张图本质上所有的点计算出的相机位姿应该都是相同的,但这是不可能的,一张图会有很多个特征点。上面的第一个非零项就是i张图片的第j个特征点算出的误差对于扰动小量的偏导,第二个非零项是误差对于特征点的导数(特征点的位置也是可以微调的,因为位姿如果变了,特征点不也会变的吗?因此可以把它也当成优化变量)
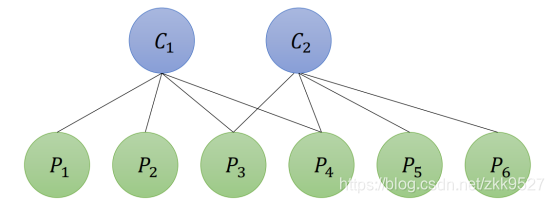
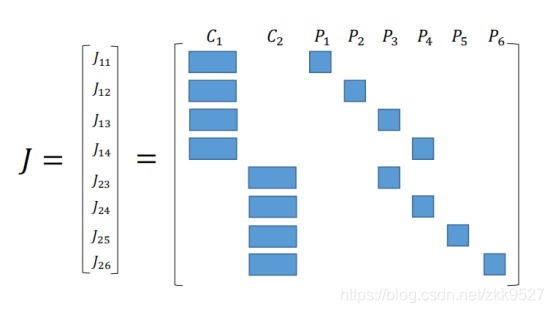
高博书里就举了个例子,假如相机在两个位置C1和C2,看到特征点的情况如图:
那么雅克比矩阵就长这样:
里面的空缺就是0,原因很显然,第一个相机关于第一个特征点产生的投影误差,不可能受第二个相机影响。上面的J矩阵,每一行例如第四行J14,就是第一个相机位置拍摄的图片中的第四个特征点,根据外参畸变内参计算到像素坐标的时候产生的误差对于相机的位姿和特征点产生的导数。
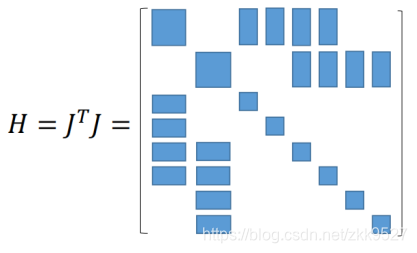
那么它的自身转置与它的乘积,就长得像一个箭头。
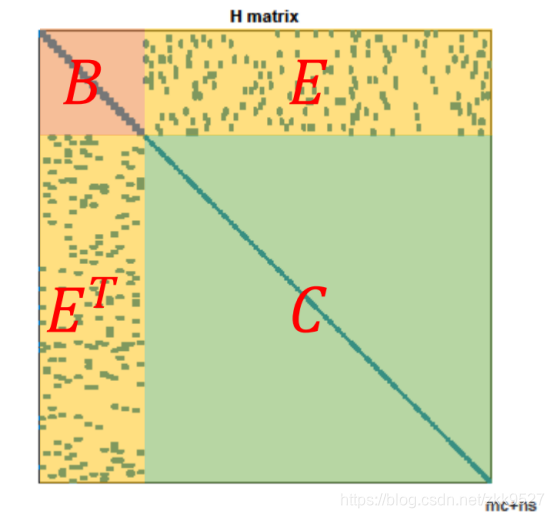
这个箭头形的矩阵可以这么划分:
所以就是求解下面的方程:
到目前为止,还没有利用它的稀疏特性。虽然C是稀疏的,但是ET这里不稀疏啊,这个矩阵求解会十分困难。高博处理的方式是把左上角E的东西统统处理到B那里:
这样乘完就是:
右上角变成了0,构造的方程就是:
这样就变成一个一元一次方程,左上角那块大小很小,求这个小块比求整体的大块容易,这样达到快速求解的方式。
算出△xc了,再代入算△xp。(高博说这个方式叫schur消元。这学期我们也在上矩阵与数值计算(这个课十分之抽象),里面也有schur分解,但是貌似schur分解和schur消元不是一码事。他说这个叫“边缘化”,意思是本身是同时求解两个未知数,现在是分成了两个一元一次方程,先求一个再求另一个。)
之后书里的内容就是讲这个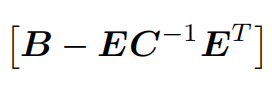
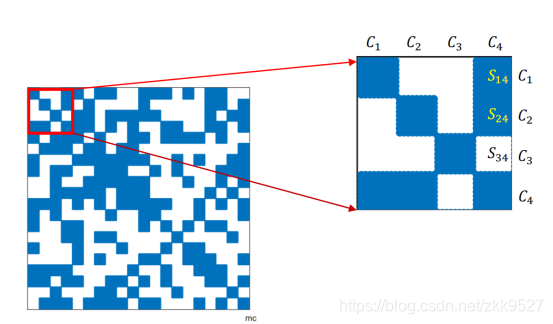
上面的这个蓝色白色矩阵,这就是H矩阵的左上角,左上角都是相机位姿,因此这个蓝色白色矩阵的x轴和y轴都是相机位姿,它是个对称矩阵,蓝色区域就代表两个位置有共同观测点,白色就代表没有共同观测点。
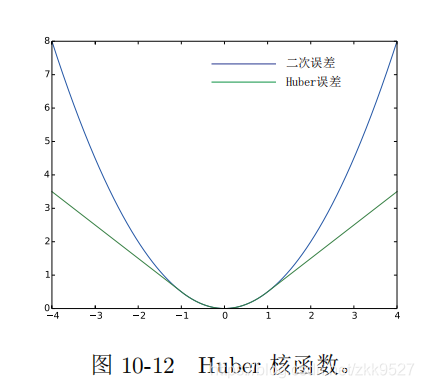
鲁棒核函数:
这个意如其名,比较鲁棒,把误差限制在一个范围内才进行二次增长,超过阈值就变成一次增长,以防一个误匹配使劲优化,把整体都给带歪了。
图优化的内容是讲代码,这个我这第二轮复习先不深究,先欠着,之后补充。
位姿图(Pose Graph)
这就进入了第11讲,后端2。这章的内容依旧是实践为重点,我这里主要讲到的公式推导,因为我看的时候花了点时间,所以把它写下来。
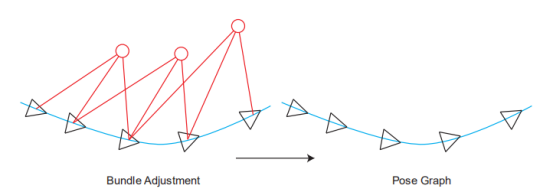
BA和图优化,是把位姿和空间点放在一块,进行优化。特征点非常多,机器人轨迹越走越长,特征点增长的也很快。因此位姿图优化的意义在于:在优化几次以后把特征点固定住不再优化,只当做位姿估计的约束,之后主要优化位姿。
也就是说,不要红色的路标点了,只要位姿。位姿里的三角形是位姿,蓝色的线是两个位姿之间的变换。
【关于这点,有一个理解非常重要:三角形的位姿,是通过和世界坐标系的比较而得到的,其实世界坐标系在大部分情况下也就是一开机的时候的相机坐标系,把第一帧检测到的特征点的相机坐标,当成是世界坐标,以此为参照,逐步直接递推下去。而上图蓝色的线,是根据中途的两张图,单独拿它俩出来估计一个相对的位姿变换。
换言之:在前端的匹配中,基本都是世界坐标系的点有了,然后根据图像坐标系下的点,估计世界坐标系与图像坐标系下的变换关系作为位姿,(这里的世界坐标系下的坐标实际是根据第一帧一路递推下来的,可能错误会一路累积)我们假设算出来两个,分别是T1和T2。而蓝色的线,作为两个位姿之间的相对变换,也就是T1和T2之间的变换。但它并不是直接根据T1的逆乘以T2这种数学方式算出来的(不然还优化什么?肯定相等啊)而是通过T1和T2所在的图像进行匹配,比如单独算一个2D-2D之间的位姿变换或者光流法等,这样根据图像算出的位姿很有可能是和T1与T2用数学方式计算得到的位姿是有差异的(因为没有涉及到第一帧图像,就是单纯这两张图像的像素坐标)。这个理论一定要明白,不然纯粹是瞎学】
开始公式推导了,没看懂书上推导的可以看我这里的讲解:
先列一个李群的变换:
这个△的意思就是蓝色的边,两个位姿i和j之间的变换ij。
高博就把它乘到右边,那么左边就是1,求对数是0,通过这种方式来构造一个误差,使它为0:
想求误差对于位姿Ti的偏导数和位姿Tj的偏导数,从李代数的角度出发,给俩左扰动,一个是i的小扰动δξi,一个是j的δξj。不过Ti在误差函数里是逆矩阵,求了逆以后,i的小扰动δξi就去了右边:
然后套用第四讲里的伴随性质:
为什么要套用这个性质呢,是因为是想把eij里面最右边的那个Tj从右边一路移到左边去:
之后的推导过程就缺乏讲解,我这里补充上:
1.把两个exp合并起来,然后泰勒展开,保留一阶项:(这个泰勒展开还不记得的人就放弃slam吧)
2.这也就是最缺少的一步,书里直接就得到了:
不熟的人会百思不得其解,这特么怎么算的?偏偏b站之类的网课上面,到这一章的内容就没了,我第一次看的时候就卡到了这里。实际是乘开再用第四章的BCH近似来做。我在纸上展示一下推导过程吧(字比较难看不要怪罪):
(注:我这个推导已经被网友指出是错误的,本来应该删掉,但是还是放在这里给大家做一个错误的样例,这种思路是不对的:)
对于这块还看不太明白的,可以自己模仿这个思路推一下,对此有几点说明:
1.最后约等于的第一项eij,并不是三个T乘进去得到的,事实上根据李代数BCH近似,最后有三个eij,两正一负合并得到的。
2.两个微分是怎么就是微分了?答:因为李代数那章,雅克比矩阵J本身代表的意思就是对李群的微分(求它的导数相当于左乘或右乘一个雅克比矩阵)
3.其实我也不能保证我的推导百分百正确,大家做一个参考吧。尤其是里面的三项,本身是相加再求对数Ln,其实感觉应该是Ln里面三项相乘才能拆开,里面三项相加怎么拆开?如果我的推导有毛病,应该就是这里有点毛病。不过以我目前的了解,不知道再该如何解释这步推导了,因此先暂时当它正确,欢迎大家评论留言指出错误。
注:这点已经有网友 甲板凳子(博客地址:点击这里)私信指出来了,我认为他的是对的,我的推导不对:Ln内部三项相加不能拆开。他的解法如下:
最后高博解释把J作一个近似:
最后再总结下:第一,先由两个位姿顶点Ti和Tj、一个位姿变换边Tij构成一个优化函数,第二,扰动该函数并对两个位姿顶点的扰动量求偏导,得到J,然后计算H,第三,根据H△x=g得到扰动量△x,并对原先俩位姿进行更新,实现优化。(这点总结比较重要,不想清楚的话很容易在繁琐的推导中迷失掉,因此这里我们又有了一个新的认识,“前端”关注的是光度误差与重投影误差之类的东西,而这里“后端”关注的是已经知道了不同的位姿T,如何整体对它进行调整,这也就更符合了“后端”的含义)
把所有的顶点和边都考虑进来,总的目标函数就是:
因子图优化:
这章还有个内容是因子图优化。这部分带着星号。这部分内容可能比较难,所以书里介绍了个大概。
但是我们不应该看到带星号就跳过。作为自主学习,毕竟不是考试,学到的东西都是自己的,因此懂得越多越好。何况,看这个书的基本都是硕士以上,概率的东西都学烂掉了,不应该跳过。
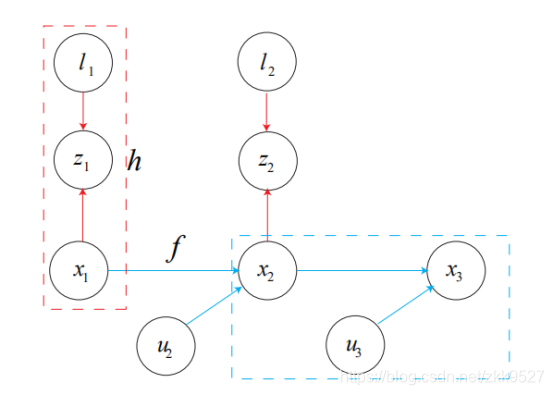
先放一个贝叶斯图:
这图的意思是,路标l和位姿x1,在状态方程h的作用下一起决定了一个观测数据z。
位姿x1根据运动方程f和噪声u2一起构成了下一步的位姿x2,这个过程逐步递推。红框表示一次观测,蓝框表示一次运动。
(注意说一句,我这里用的是我加的一个群里的电子版slam十四讲,可能是之前高博的初步版本。我文章里的所有的公式都是截的里面的图。在纸质书的地方,这块有错误,因为书是黑白的,编辑在语句上换成了实线框和虚线框,但是图片里面却还是两个虚线框)
蓝色框可以写成:
红框可以写成:
这就很奇妙的和卡尔曼滤波器的内容(SLAM14讲学习笔记(六)后端(最难一章:卡尔曼滤波器推导、理解以及扩展))串起来了,蓝框可以看成是先验,红框是似然,在似然和先验的共同作用下,才能得到后验,因此后端优化的目的,就是最大化后验概率,最大化后验概率是通过最大化似然概率达到的:
通过进一步观察,发现最大后验概率由许多因子乘积而成,因此贝叶斯网络可以转化乘一个因子图(Factor Graph)。
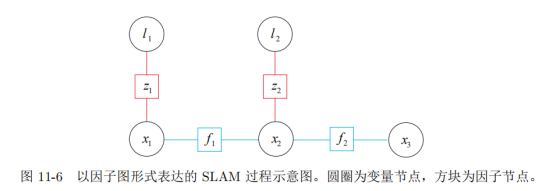
上面的贝叶斯图变成因子图长这样:
用圆圈表示变量,这里的变量是 SLAM中待优化的部分,即相机位姿 x 和路标 l,而没有观测 z 和输入 u——因为这几个量是给定的而不是待优化的。所谓因子图优化,就是调整各变量的值,使因子乘积最大化。变量的概率取成高斯分布的形式。书上给了形式我就不再列了,应该推导完卡尔曼滤波器的人看这个会觉得非常之简单。
当然看到这里,大部分人会有一个疑惑,高博也指出了,因子图优化是否就是普通图优化换了种说法?不是。
区别在于:因子图是增量的处理后端优化。啥意思呢,机器人是运动的,不同的边和节点会被不断加入图中。每加入一个点,普通图优化是对整个图进行优化,所以比较麻烦和耗时。因子图的话相当于是保留中间结果,每加入一个点,对不需要重新计算的就直接用之前的中间结果,对需要重新计算的再去计算。以这种方式加速计算,避免冗余计算。
最后从宏观上总结一下不同后端方式的差异(虽然后端分为两节,但是实际上有五种优化方式):
1.卡尔曼滤波器:从k-1时刻后验推k时刻先验,从k时刻先验推k时刻后验;
2.扩展卡尔曼滤波器:对卡尔曼滤波器进行修正,针对不是线性的情况,采用一阶泰勒展开近似线性。
3.BA优化:把一路上的所有坐标点与位姿整体放在一起作为自变量进行非线性优化
4.PoseGraph优化:先通过一路递推方式算出的各点位姿,通过数学方式计算得到一个位姿的变换A,再通过单独拿出两张图像来算出一个位姿变换B,争取让B=A
5.因子图优化:保留中间结果,每加入一个点,对不需要重新计算的就直接用之前的中间结果,需要重新计算的再去计算,从而避免冗余计算。