【模型】GRU模型详解

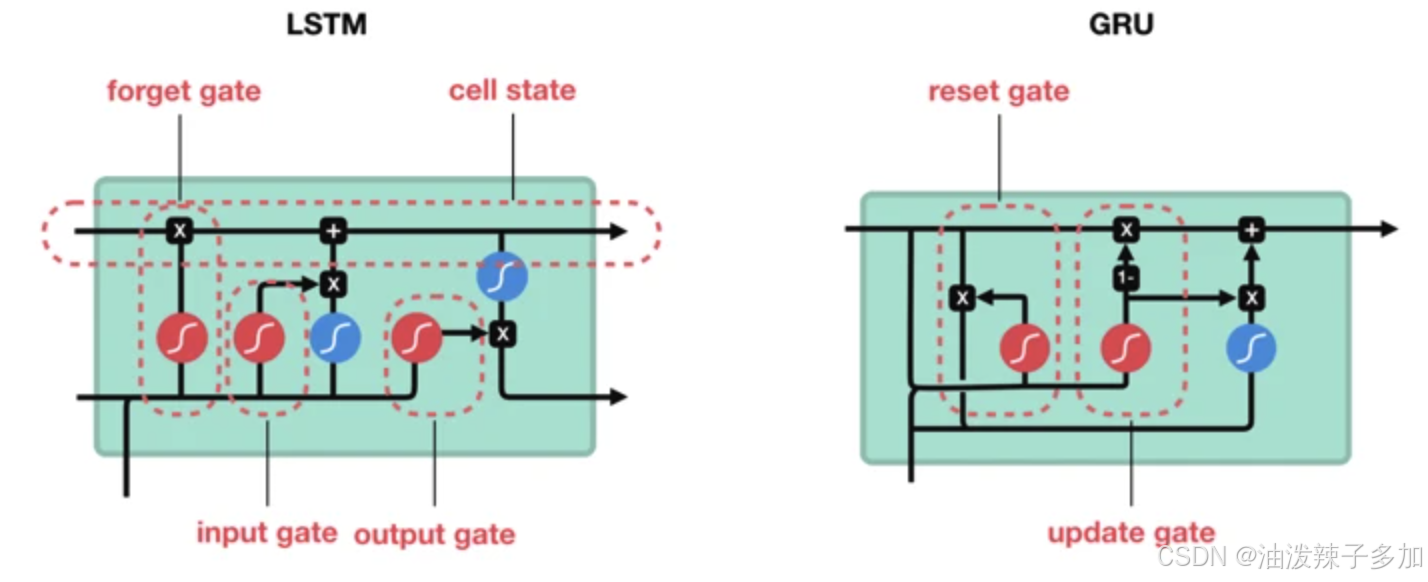
1. GRU 模型架构

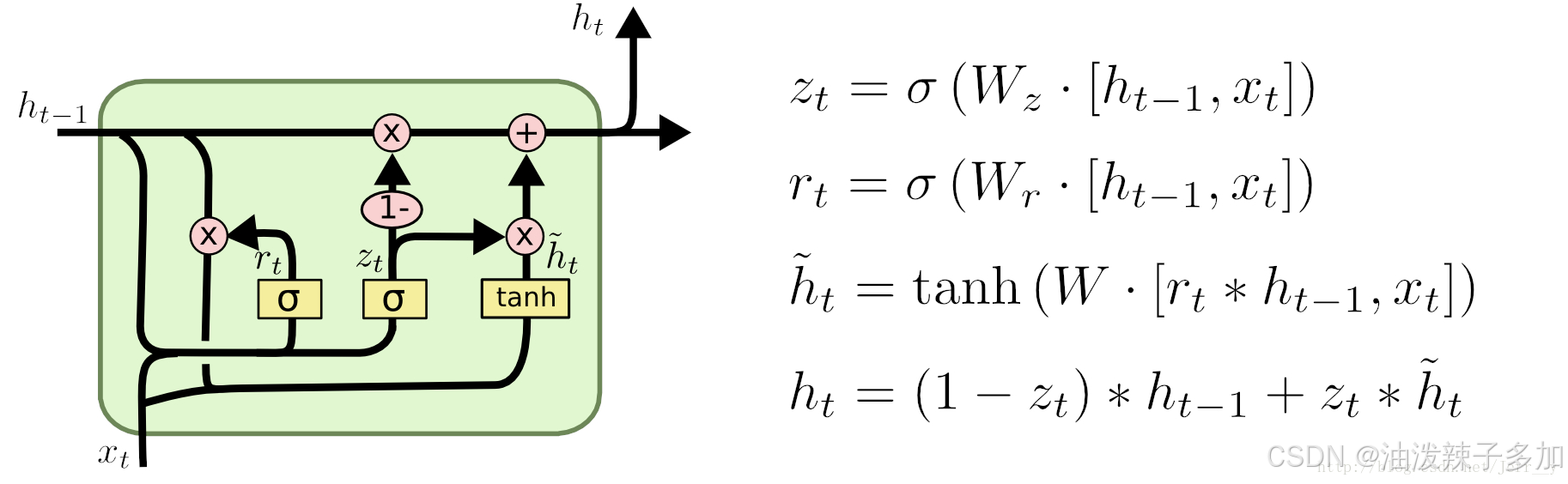
在这里插入图片描述

GRU 模型包含两个主要的门控机制：更新门（Update Gate）和重置门（Reset Gate）。其计算过程如下：
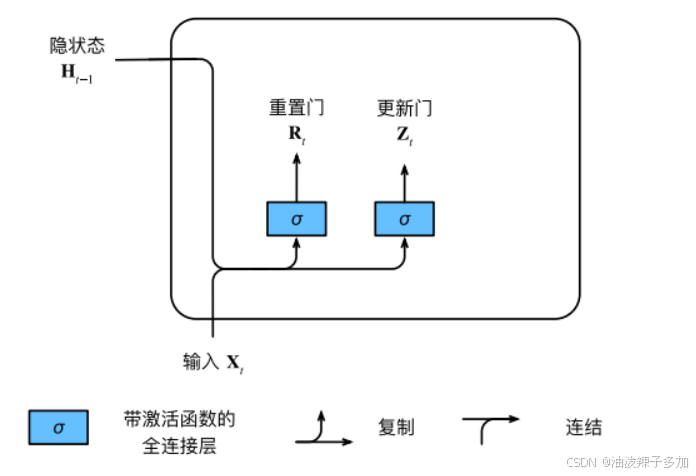
在这里插入图片描述

1.1 重置门：

决定当前隐藏状态与之前隐藏状态的相关程度。它通过一个 Sigmoid 函数输出一个范围在 [0, 1] 之间的值，表示当前时间步要忘记多少之前的信息。
$\sigma(W_r \cdot [h_{t-1}, x_t] + b_r)$
其中：

$r_t$ 是重置门的输出；
$h_{t-1}$ 是上一时刻的隐藏状态；
$x_t$ 是当前时刻的输入；
$\sigma$ 是 Sigmoid 激活函数。

1.2 更新门：

控制当前时间步的隐藏状态更新的程度。它的输出也是一个 [0, 1] 之间的值，决定当前时刻的信息有多少来自于之前的状态。

$\sigma(W_z \cdot [h_{t-1}, x_t] + b_z)$
其中：

$z_t$ 是更新门的输出。

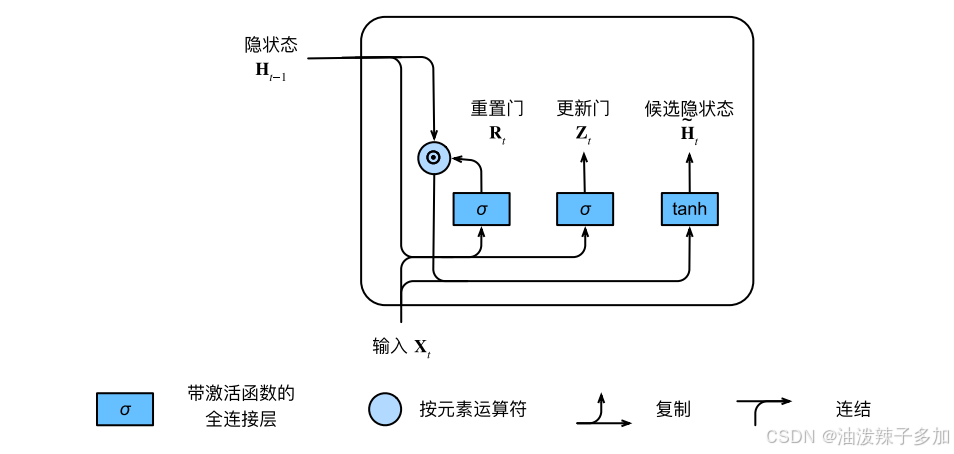
1.3 候选隐藏状态：

计算当前时刻的候选隐藏状态，候选状态结合了当前输入和重置门的影响。
$\tilde{h_t}= \tanh(W_h \cdot [r_t \odot h_{t-1}, x_t] + b_h)$
其中：

$\tilde{h_t}$ 是候选隐藏状态；
$\odot$ 表示按元素相乘， $\tanh$ 是双曲正切激活函数。

1.4 最终隐藏状态：

根据更新门的值和上一时刻的隐藏状态与当前时刻的候选隐藏状态，最终计算出当前的隐藏状态。

$h_t= (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h_t}$

2. Pytorch 实现

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from sklearn.metrics import mean_squared_error
from torch.utils.data import DataLoader, TensorDataset
import matplotlib.pyplot as plt

# 定义GRU模型类
class GRU(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, forecast_horizon):
        super(GRU, self).__init__()
        
        self.num_layers = num_layers
        self.input_size = input_size
        self.hidden_size = hidden_size        
        self.forecast_horizon = forecast_horizon
        # GRU层
        self.gru = nn.GRU(input_size=self.input_size, hidden_size=self.hidden_size,
                          num_layers=self.num_layers, batch_first=True)
        
        # 全连接层1
        self.fc1 = nn.Linear(self.hidden_size, 20)
        # 全连接层2
        self.fc2 = nn.Linear(20, self.forecast_horizon)
        
        # Dropout层，用于防止过拟合
        self.dropout = nn.Dropout(0.2)

    def forward(self, x):
        # 初始化隐藏状态并确保其在GPU上
        h_0 = torch.randn(self.num_layers, x.size(0), self.hidden_size).to(device)
        
        # 通过GRU层进行前向传播
        out, _ = self.gru(x, h_0)
        
        # 通过全连接层和激活函数
        out = F.relu(self.fc1(out[:, -1, :]))  # 只取最后一个时间步的输出
        out = self.fc2(out)  # 输出层
        return out

# 设置设备，使用GPU（如果可用）
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f'Using device: {device}')

# 将数据转换为torch tensors，并转移到设备（GPU/CPU）
X_train_tensor = torch.Tensor(X_train).to(device)
X_test_tensor = torch.Tensor(X_test).to(device)

y_train_tensor = torch.Tensor(y_train).squeeze(-1).to(device)
y_test_tensor = torch.Tensor(y_test).squeeze(-1).to(device)

# 创建训练数据和验证数据集
train_dataset = TensorDataset(X_train_tensor, y_train_tensor)
test_dataset = TensorDataset(X_test_tensor, y_test_tensor)

# 定义 DataLoader
batch_size = 512
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)

# 初始化RNN模型
input_size = X_train.shape[2]  # 特征数量
hidden_size = 64  # 隐藏层神经元数量
num_layers = 2  # RNN层数
forecast_horizon = 5  # 预测的目标步数

model = GRU(input_size, hidden_size, num_layers, forecast_horizon).to(device)

def train_model_with_dataloader(model, train_loader, test_loader, epochs=50, lr=0.001):
    # 定义损失函数和优化器
    criterion = nn.MSELoss()
    optimizer = optim.Adam(model.parameters(), lr=lr)
    
    train_loss = []
    val_loss = []
    
    for epoch in range(epochs):
        # 训练阶段
        model.train()
        epoch_train_loss = 0
        for X_batch, y_batch in train_loader:
            optimizer.zero_grad()
            
            # 前向传播
            output_train = model(X_batch)
            
            # 计算损失
            loss = criterion(output_train, y_batch)
            loss.backward()  # 反向传播
            optimizer.step()  # 更新参数
            
            epoch_train_loss += loss.item()  # 累计批次损失
            
        train_loss.append(epoch_train_loss / len(train_loader))  # 计算平均损失
        
        # 验证阶段
        model.eval()
        epoch_val_loss = 0
        with torch.no_grad():
            for X_batch, y_batch in test_loader:
                output_val = model(X_batch)
                loss = criterion(output_val, y_batch)
                epoch_val_loss += loss.item()
        
        val_loss.append(epoch_val_loss / len(test_loader))  # 计算平均验证损失
        
        # 打印日志
        if (epoch + 1) % 100 == 0:
            print(f'Epoch [{epoch+1}/{epochs}], Train Loss: {train_loss[-1]:.4f}, Validation Loss: {val_loss[-1]:.4f}')
    
    # 绘制训练损失和验证损失曲线
    plt.plot(train_loss, label='Train Loss')
    plt.plot(val_loss, label='Validation Loss')
    plt.title('Loss vs Epochs')
    plt.xlabel('Epochs')
    plt.ylabel('Loss')
    plt.legend()
    plt.show()

def evaluate_model_with_dataloader(model, test_loader):
    model.eval()
    y_pred_list = []
    y_test_list = []
    
    with torch.no_grad():
        for X_batch, y_batch in test_loader:
            y_pred = model(X_batch)
            y_pred_list.append(y_pred.cpu().numpy())
            y_test_list.append(y_batch.cpu().numpy())
    
    # 将所有批次结果拼接
    y_pred_rescaled = np.concatenate(y_pred_list, axis=0)
    y_test_rescaled = np.concatenate(y_test_list, axis=0)
    
    # 计算均方误差
    mse = mean_squared_error(y_test_rescaled, y_pred_rescaled)
    print(f'Mean Squared Error: {mse:.4f}')
    
    return y_pred_rescaled, y_test_rescaled

# 训练模型
train_model_with_dataloader(model, train_loader, test_loader, epochs=2000)

# 评估模型性能
y_pred_rescaled, y_test_rescaled = evaluate_model_with_dataloader(model, test_loader)

# 保存模型
def save_model(model, path='./model_files/multistep_gru_model.pth'):
    torch.save(model.state_dict(), path)
    print(f'Model saved to {path}')

# 保存训练好的模型
save_model(model)

1.代码解析

（1）验证loss

model.eval()
with torch.no_grad():
	output_val = model(X_test)
	val_loss_value = criterion(output_val, y_test)
	val_loss.append(val_loss_value.item())

model.eval()将模型设置为评估模式，调用 eval() 方法会禁用Dropout 和 Batch Normalization
- Dropout：在训练时会随机丢弃一部分神经元，以避免过拟合，但在评估时，我们需要使用整个网络来进行推理。
- Batch Normalization：在训练时会计算每个小批量的均值和方差来进行标准化，而在评估时会使用在训练时计算得到的总体均值和方差。
torch.no_grad() 是一个上下文管理器，用于在该代码块内禁用梯度计算。通常在推理阶段，模型的参数不再更新，因此不需要计算梯度，这可以节省内存和加速推理；
val_loss_value.item() 提取损失值 val_loss_value 的数值部分，将其转换为 Python 的标量类型（float），因为 val_loss_value 是一个包含梯度信息的张量；
val_loss.append(...) 将每个批次（或每个 epoch）计算得到的损失值追加到 val_loss 列表中，用于记录每次验证的损失，可以用于后续的性能分析和绘制损失曲线；

3. GRU 的优缺点

3.1 优点

较少的参数：GRU 比 LSTM 更简单，参数较少，计算效率更高。
较快的训练速度：GRU 的门结构较简单，因此训练时间比 LSTM 更短。
长距离依赖建模：GRU 能够有效地捕捉时间序列数据中的长距离依赖，解决传统 RNN 的梯度消失问题。

3.2 缺点

性能不如 LSTM：在一些复杂任务中，LSTM 可能比 GRU 更强大，尤其是在处理更复杂的时间序列任务时。
较少的控制：GRU 只有两个门（与 LSTM 的三个门相比），可能在某些情况下缺乏足够的灵活性。

4. GRU 的算法变种

Bi-GRU (双向 GRU)：双向 GRU 同时在正向和反向传播序列信息，增强了模型的表现。
Attention-based GRU：结合注意力机制，使得模型可以更加关注输入序列中重要的部分，提升序列建模能力。
Deep GRU：通过堆叠多个 GRU 层来构建更深的模型，增加模型的学习能力。

5. GRU 的特点

简洁高效：GRU 相比 LSTM 更简洁，计算效率更高，尤其在内存受限的环境中更具优势。
强大的时间序列建模能力：能够捕捉时间序列中的长期依赖，适合需要时序特征学习的任务。
灵活性：可以与其他网络架构（如卷积神经网络、Transformer 等）结合使用，提升模型表现。

6. 应用场景

时间序列预测：如股市、气象、交通流量等数据的预测。
自然语言处理：如机器翻译、语音识别、情感分析等。
视频分析：如视频中的动作识别、视频分类等任务。
序列标注任务：如命名实体识别（NER）、词性标注（POS）、语音识别中的声学建模等。