一、 实验目的和要求
内容:
编程随机生成n个结点的无向图并能进行(半)欧拉图的判定,若是则给出欧拉(回)路。
要求:
对给定n个结点,随机生成邻接矩阵以确定某无向简单图并进行欧拉图和半欧拉图的判定,若符合则给出至少一条欧拉回路或欧拉路。
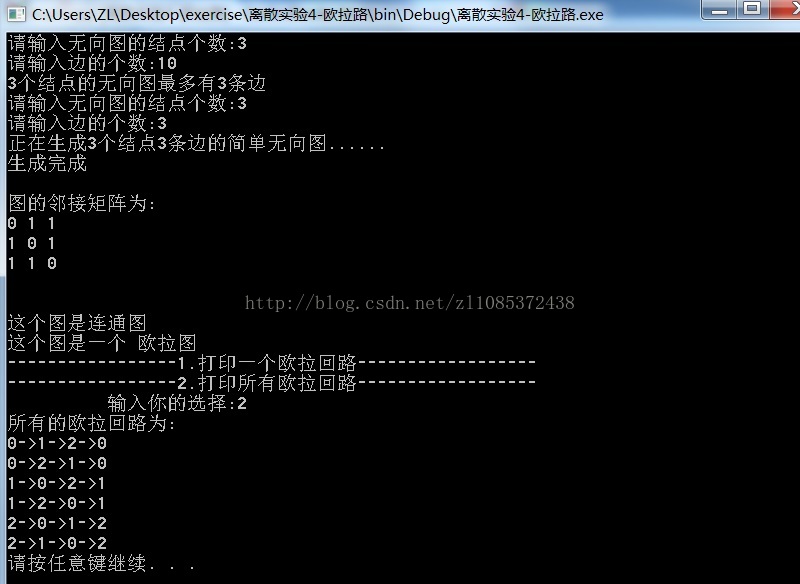
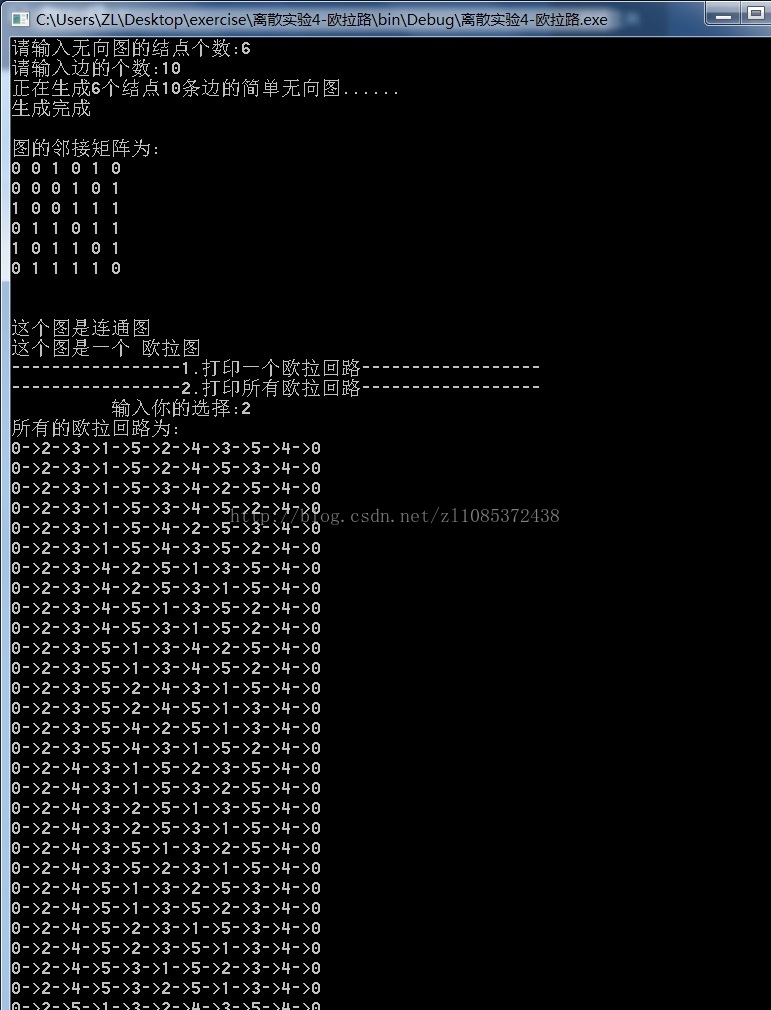
程序的能够根据输入的n和m,随机生成具有n个结点m个边的简单无向图(能够判断n和m的合理性),然后判断图的连通性,如果这个图是个连通图,再计算图中度数是奇数的结点个数,判断是欧拉图还是半欧拉图,如果是欧拉图或者半欧拉图,然后根据输入打印一个欧拉(回)路,或者所有的欧拉(回)图。
#include <iostream>
#include <cstdio>
#include <ctime>
#include <cstdlib>
#define Size 1000
using namespace std;
int n,m;
int G[Size][Size];
void Generate() //随机生成图
{
printf("正在生成%d个结点%d条边的简单无向图......\n",n,m);
int cnt=0;
srand(time(NULL));
while(cnt<m)
{
int x=rand()%n;
int y=rand()%n;
if(x!=y && G[x][y]==0)
{
G[x][y]=1;
G[y][x]=1;
cnt++;
}
}
printf("生成完成\n\n");
if(n<=10)
{
printf("图的邻接矩阵为:\n");
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
printf("%d ",G[i][j]);
}
printf("\n");
}
printf("\n");
}
}
int Judge() //判断(半)欧拉图
{
int flag=0;
for(int i=0;i<n;i++)
{
int cnt=0;
for(int j=0;j<n;j++)
{
if(G[i][j]==1)
{
cnt++;
}
}
if(cnt%2==1)
{
flag++;
}
}
if(flag==0)
{
return 0; //欧拉回路
}
else if(flag==2)
{
return 1; //欧拉路
}
else
{
return -1; //不是欧拉路也不是欧拉回路
}
}
int P[Size][Size]; //可达性矩阵
int T[Size][Size]; //临时存放G的n次方的矩阵
int TT[Size][Size];
int JudgeLianTong() //判断连通性
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
P[i][j]=G[i][j];
T[i][j]=G[i][j];
}
}
for(int k=2;k<=n;k++) //n的4次方复杂度,计算可达性矩阵
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
int t=0;
for(int a=0;a<n;a++)
{
t+=T[i][a]*G[a][j];
}
if(t==0)
{
TT[i][j]=0;
}
else
{
TT[i][j]=1;
}
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
T[i][j]=TT[i][j];
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(T[i][j]>0 || P[i][j]>0 )
{
P[i][j]=1;
}
}
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(i!=j && P[i][j] ==0)
{
return 0;
}
}
}
return 1;
}
int choice,has;
int vis[Size][Size];
int record[Size];
int cnt;
void FindLu(int cur)
{
if(choice==1 && has==1) return;
if(cnt==m+1)
{
for(int i=0;i<cnt;i++)
{
if(i==0) printf("%d",record[i]);
else printf("->%d",record[i]);
}
printf("\n");
has=1;
}
else
{
for(int i=0;i<n;i++)
{
if(G[cur][i]==1 && vis[cur][i]==0 )
{
vis[i][cur]=vis[cur][i]=1;
record[cnt++]=i;
FindLu(i);
cnt--;
vis[i][cur]=vis[cur][i]=0;
}
}
}
}
int main()
{
do
{
printf("请输入无向图的结点个数:");
scanf("%d",&n);
printf("请输入边的个数:");
scanf("%d",&m);
if(m>n*(n-1)/2)
{
printf("%d个结点的无向图最多有%d条边\n",n,n*(n-1)/2);
}
}while(m>n*(n-1)/2); //判断n和m的合理性
Generate(); //随机生成图
if(JudgeLianTong()==0) //判断连通性
{
printf("这个图不是一个连通图,所以也不是欧拉图和半欧拉图\n");
}
else
{
printf("\n这个图是连通图\n");
int tmp=Judge(); //判断(半)欧拉图
if(tmp==0)
{
printf("这个图是一个 欧拉图\n");
printf("-----------------1.打印一个欧拉回路------------------\n");
printf("-----------------2.打印所有欧拉回路------------------\n");
printf(" 输入你的选择:");
scanf("%d",&choice);
if(choice==1)
{
printf("其中一条欧拉回路为:\n");
record[cnt++]=0;
FindLu(0); //找出回路
cnt--;
}
else if(choice==2)
{
printf("所有的欧拉回路为:\n");
for(int i=0;i<n;i++)
{
record[cnt++]=i;
FindLu(i);
cnt--;
}
}
else
{
printf("-----------------输入有误-----------------\n");
system("pause");
}
}
else if(tmp==1)
{
printf("这个图是一个 半欧拉图\n");
printf("-----------------1.打印一个欧拉路------------------\n");
printf("-----------------2.打印所有欧拉路------------------\n");
printf(" 输入你的选择:");
scanf("%d",&choice);
if(choice==1)
{
for(int i=0;i<n;i++)
{
int t=0;
for(int j=0;j<n;j++)
{
if(G[i][j]==1)
{
t++;
}
}
if(t%2==1)
{
record[cnt++]=i;
FindLu(i);
cnt--;
break;
}
}
}
else if(choice==2)
{
printf("所有的欧拉路为:\n");
for(int i=0;i<n;i++)
{
int t=0;
for(int j=0;j<n;j++)
{
if(G[i][j]==1)
{
t++;
}
}
if(t%2==1)
{
record[cnt++]=i;
FindLu(i);
cnt--;
}
}
}
else
{
printf("-----------------输入有误-----------------\n");
}
}
else
{
printf("这个图既不是欧拉图,也不是半欧拉图\n");
}
}
system("pause");
return 0;
}