一、背包问题概述
背包问题(Knapsackproblem)是⼀种组合优化的NP完全问题。
问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最⾼。
根据物品的个数,分为如下几类:
- 01背包问题:每个物品只有⼀个
- 完全背包问题:每个物品有⽆限多个
- 多重背包问题:每件物品最多有si个
- 混合背包问题:每个物品会有上⾯三种情况…
- 分组背包问题:物品有n组,每组物品里有若干个,每组里最多选一个物品
其中上述分类里面,根据背包是否装满,⼜分为两类:
- 不⼀定装满背包
- 背包⼀定装满
优化⽅案:
- 空间优化-滚动数组
- 单调队列优化
- 贪⼼优化
根据限定条件的个数,又分为两类:
- 限定条件只有⼀个:比如体积->普通的背包问题
- 限定条件有两个:比如体积+重量->⼆维费⽤背包问题
根据不同的问法,又分为很多类:
- 输出⽅案
- 求⽅案总数
- 最优⽅案
- ⽅案可⾏性
其实还有很多分类,但是我们仅需了解即可。
因此,背包问题种类非常繁多,题型非常丰富,难度也是非常难以捉摸。但是,尽管种类非常多,都是从01背包问题演化过来的。所以,⼀定要把01背包问题学好。
二、相关编程题
2.1 01背包问题
2.1.1 01背包(模板)
题目链接
【模板】01背包_牛客题霸_牛客网 (nowcoder.com)
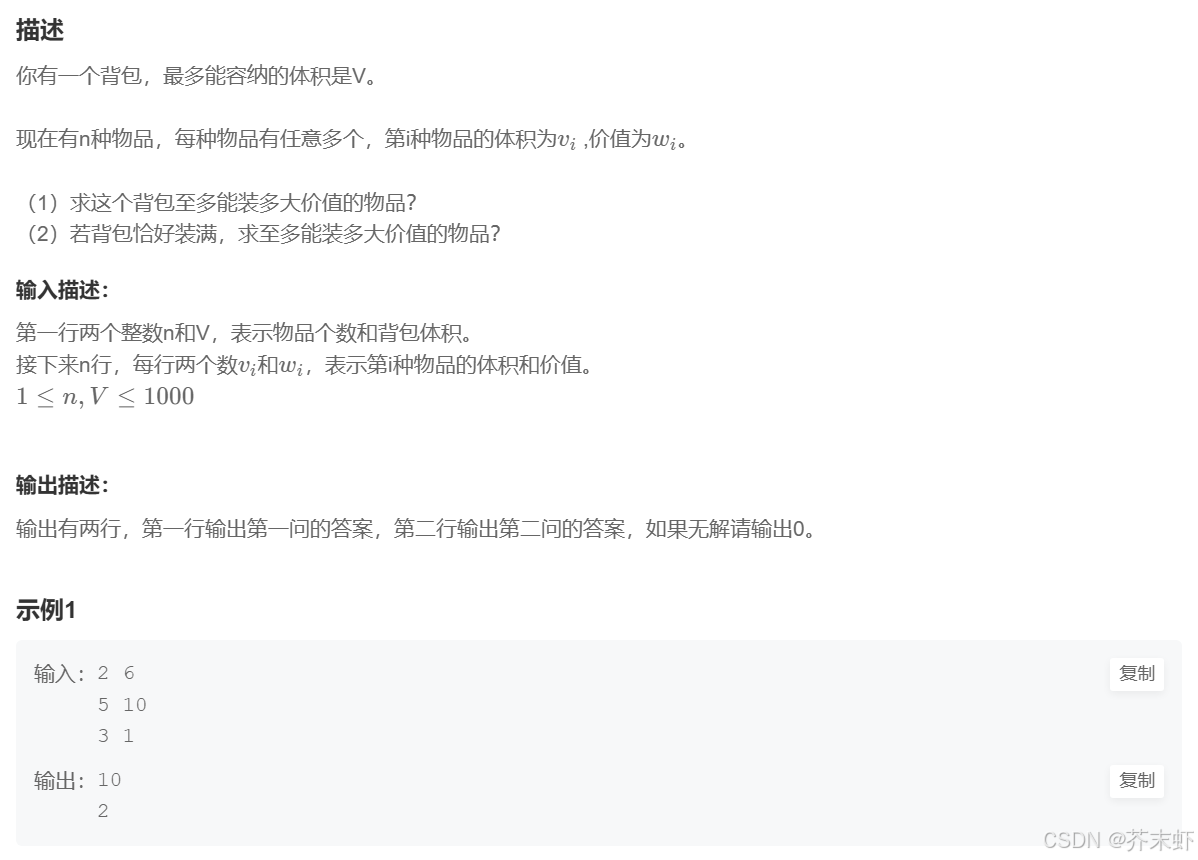
题目描述
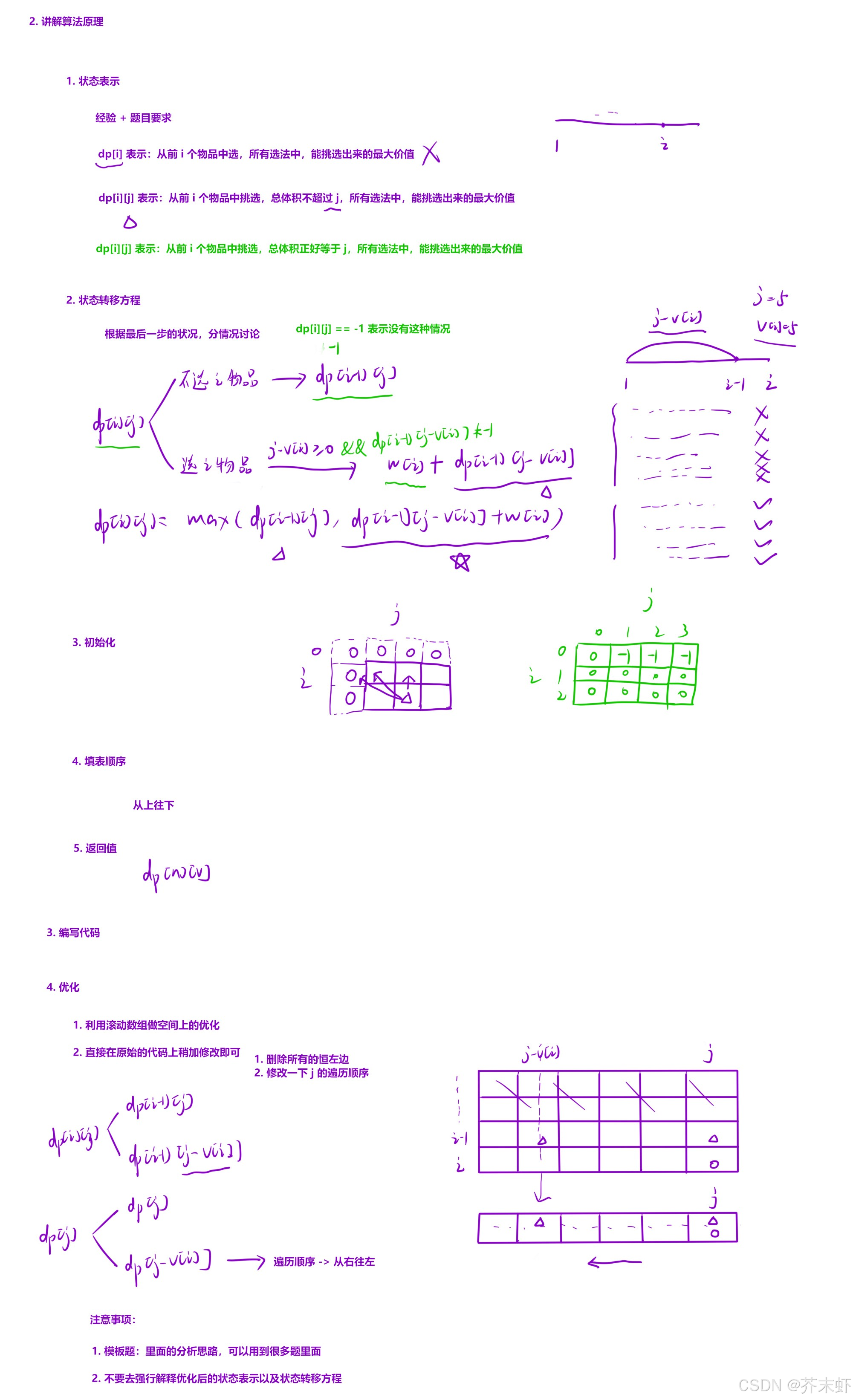
算法原理
编写代码
#include <iostream>
#include <cstring>
using namespace std;
#define N 1010
int n, V;
int v[N], w[N];
int dp[N][N];
int main() {
//读入数据
cin >> n >> V;
for(int i = 1; i <= n; ++i) //注意所有下标从1开始
{
cin >> v[i] >> w[i];
}
//解决第一问
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= V; ++j)
{
dp[i][j] = dp[i-1][j]; // 不选i物品
if(j>=v[i]) //要保证不越界,有空间存放v[i]
dp[i][j] = max(dp[i][j], w[i]+dp[i-1][j-v[i]]); //选i物品
}
}
cout << dp[n][V] << endl;
//解决第二问
memset(dp, 0, sizeof(dp));
for(int j = 1; j <= V; ++j) dp[0][j] = -1; //-1表示恰好装满体积j无解
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= V; ++j)
{
dp[i][j] = dp[i-1][j]; // 不选i物品
if(j>=v[i] && dp[i-1][j-v[i]]!=-1) //条件1保证不越界,有空间存放v[i];条件2保证恰好装满
dp[i][j] = max(dp[i][j], w[i]+dp[i-1][j-v[i]]); //选i物品
}
}
cout << (dp[n][V]==-1? 0:dp[n][V]) << endl;
}
//空间优化
int dp[N];
int main() {
//读入数据...
//解决第一问
for(int i = 1; i <= n; ++i)
{
for(int j = V; j>=v[i]; --j) //注意从右往左遍历
dp[j] = max(dp[j], w[i]+dp[j-v[i]]);
}
cout << dp[V] << endl;
//解决第二问
memset(dp, 0, sizeof(dp));
for(int j = 1; j <= V; ++j) dp[j] = -1; //-1表示恰好装满体积j无解
for(int i = 1; i <= n; ++i)
{
for(int j = V; j>=v[i]; --j)
{
if(dp[j-v[i]]!=-1)
dp[j] = max(dp[j], w[i]+dp[j-v[i]]);
}
}
cout << (dp[V]==-1? 0:dp[V]) << endl;
}
2.1.2 分割等和子集
题目链接
题目描述
算法原理
- 01背包必须装满
- 为什么不用-1标识无解?因为其状态表示中自带无解判断(false)
编写代码
//空间优化
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n = nums.size();
int sum = 0;
for(auto e : nums) sum+=e;
if(sum%2==1) return false;
vector<bool> dp(sum/2+1);
dp[0] = true;
for(int i = 1; i <= n; ++i)
{
for(int j = sum/2; j >= nums[i-1]; --j)
dp[j] = dp[j] || dp[j-nums[i-1]];
}
return dp[sum/2];
}
};
2.1.3 目标和
题目链接
题目描述
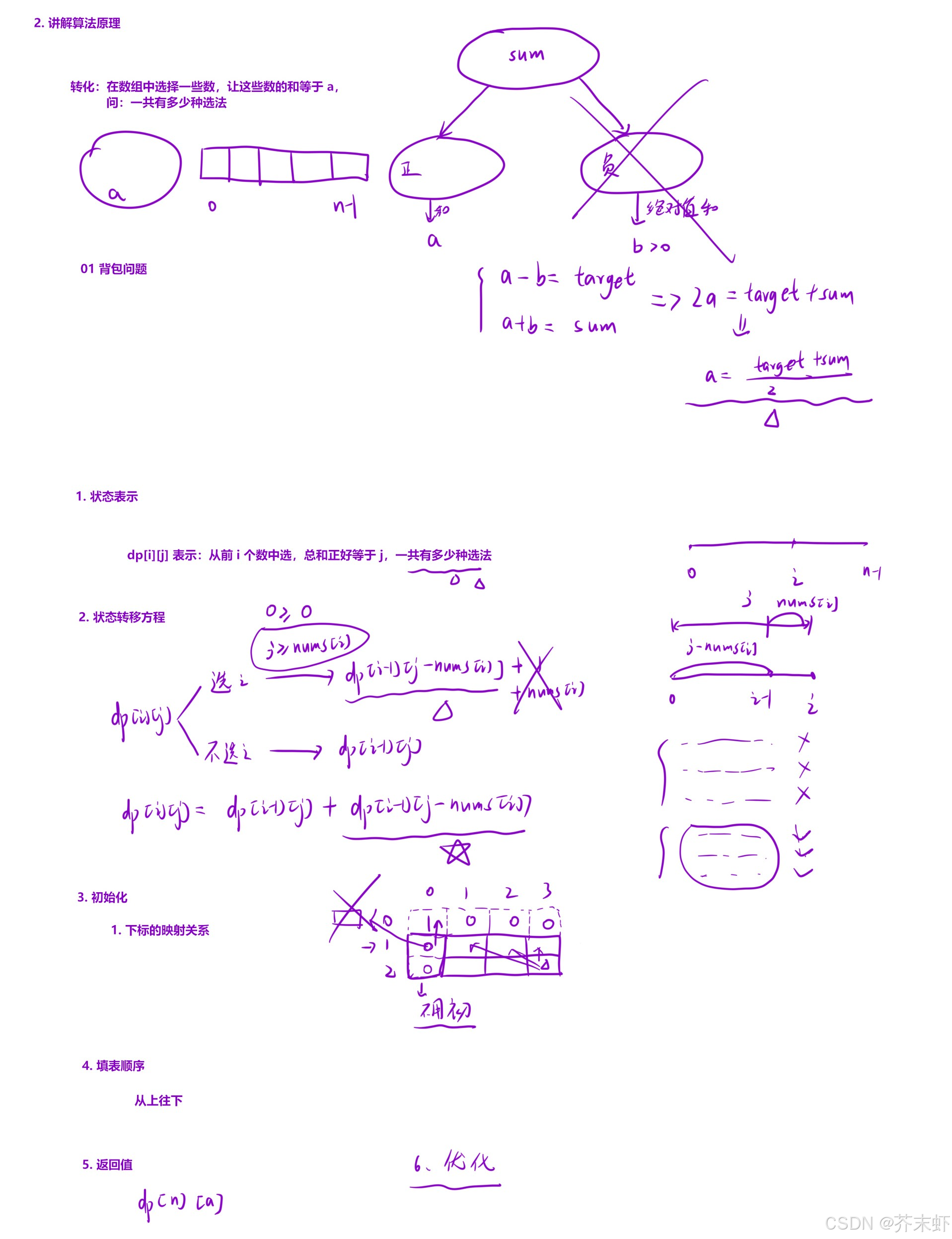
算法原理
- 01背包必须装满
- 为什么不用-1标识无解?因为其状态表示中自带无解判断(0种选法)
编写代码
//空间优化
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int n = nums.size();
int sum = 0;
for(auto e : nums) sum+=e;
int a = (sum+target)/2;
if(a<0 || (sum+target)%2==1) return false; //a是所有正数的和;必须是偶数能被2整除;
vector<int> dp(a+1);
dp[0] = 1;
for(int i = 1; i <= n; ++i)
{
for(int j = a; j >= nums[i-1]; --j)
dp[j] += dp[j-nums[i-1]];
}
return dp[a];
}
};
2.1.4 最后一块石头的重量Ⅱ
题目链接
1049. 最后一块石头的重量 II - 力扣(LeetCode)
题目描述
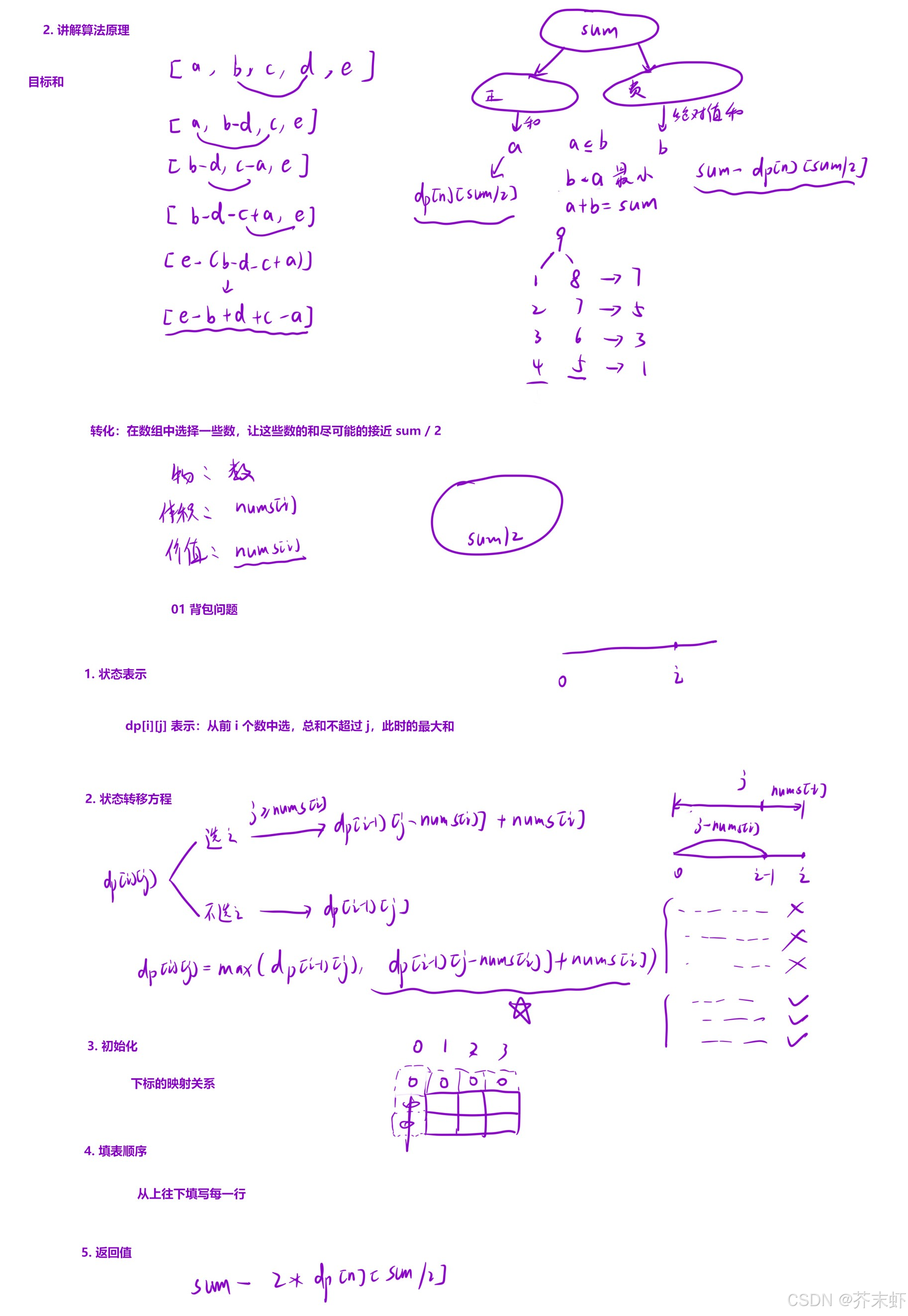
算法原理
- 01背包不必装满
编写代码
//空间优化
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int n = stones.size();
int sum = 0;
for(auto e : stones) sum+=e;
int aim = sum/2;
vector<int> dp(aim+1);
for(int i = 1; i <= n; ++i)
{
for(int j = aim; j >=stones[i-1]; --j)
dp[j] = max(dp[j], stones[i-1]+dp[j-stones[i-1]]);
}
return sum-dp[aim]*2;
}
};
2.2 完全背包问题
2.2.1 完全背包(模板)
题目链接
【模板】完全背包_牛客题霸_牛客网 (nowcoder.com)
题目描述
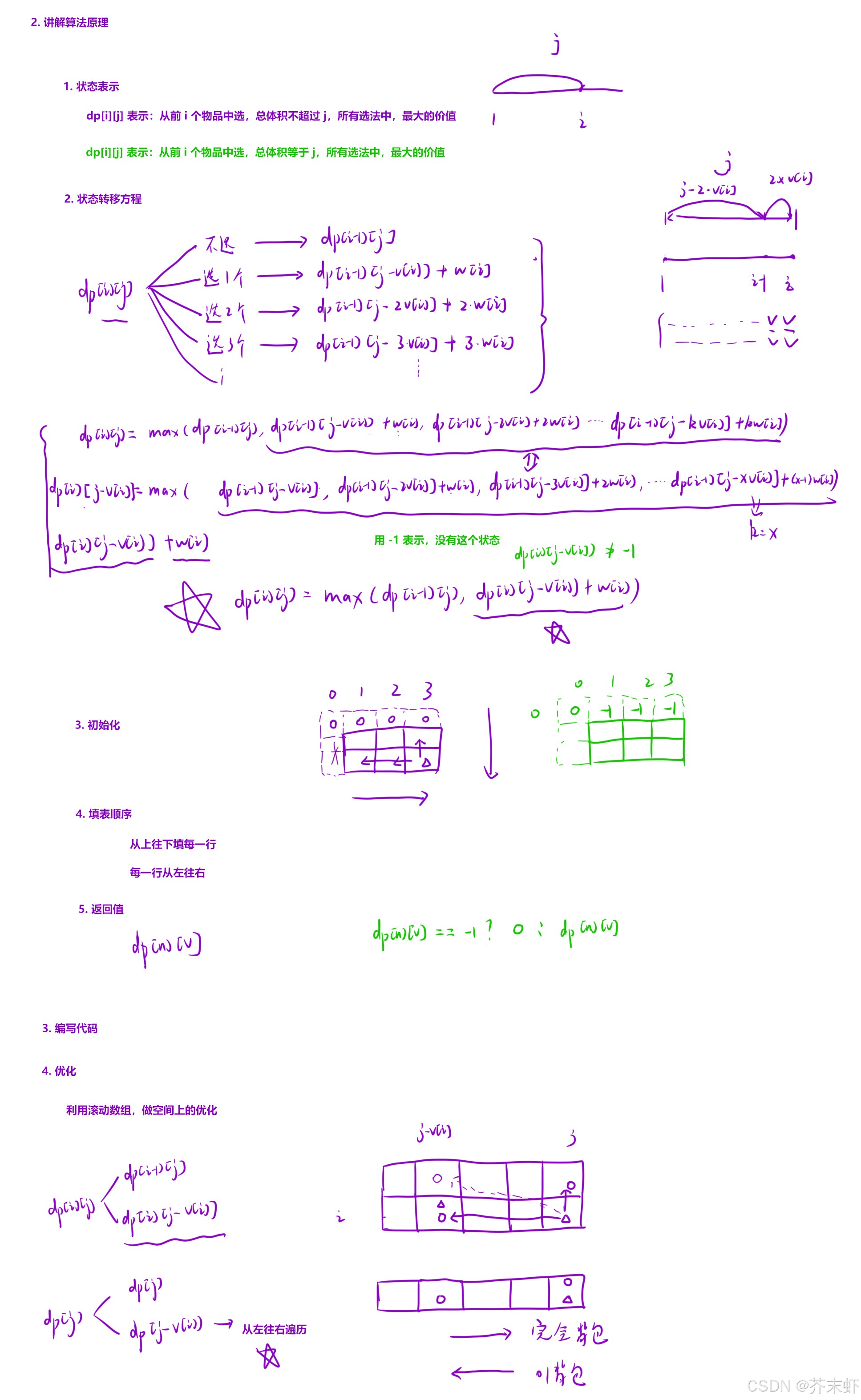
算法原理
和01背包唯一的不同点就是每个物品可以选择无数次,因此在选择i物品的状态转移方程中有所变化。
提示:综合了01背包、通配符匹配、正则表达式匹配的考点
编写代码
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
int n, V;
int v[N], w[N];
int dp[N][N];
int main() {
//读入数据
cin >> n >> V;
for(int i = 1; i <= n; ++i)
cin >> v[i] >> w[i];
//解决第一问
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= V; ++j)
{
dp[i][j] = dp[i-1][j];
if(j >= v[i])
dp[i][j] = max(dp[i][j], dp[i][j-v[i]]+w[i]);
}
}
cout << dp[n][V] << endl;
//解决第二问
memset(dp, 0, sizeof(dp));
for(int j = 1; j <= V; ++j) dp[0][j] = -1;
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= V; ++j)
{
dp[i][j] = dp[i-1][j];
if(j >= v[i] && dp[i][j-v[i]]!=-1)
dp[i][j] = max(dp[i][j], dp[i][j-v[i]]+w[i]);
}
}
cout << (dp[n][V]==-1? 0:dp[n][V]) << endl;
}
//空间优化
int dp[N];
int main() {
//读入数据...
//解决第一问
for(int i = 1; i <= n; ++i)
{
for(int j = v[i]; j <= V; ++j) //注意从左往右遍历
{
dp[j] = max(dp[j], dp[j-v[i]]+w[i]);
}
}
cout << dp[V] << endl;
//解决第二问
memset(dp, 0, sizeof(dp));
for(int j = 1; j <= V; ++j) dp[j] = -1;
for(int i = 1; i <= n; ++i)
{
for(int j = v[i]; j <= V; ++j)
{
if(dp[j-v[i]]!=-1)
dp[j] = max(dp[j], dp[j-v[i]]+w[i]);
}
}
cout << (dp[V]==-1? 0:dp[V]) << endl;
}
2.2.2 零钱兑换
题目链接
题目描述
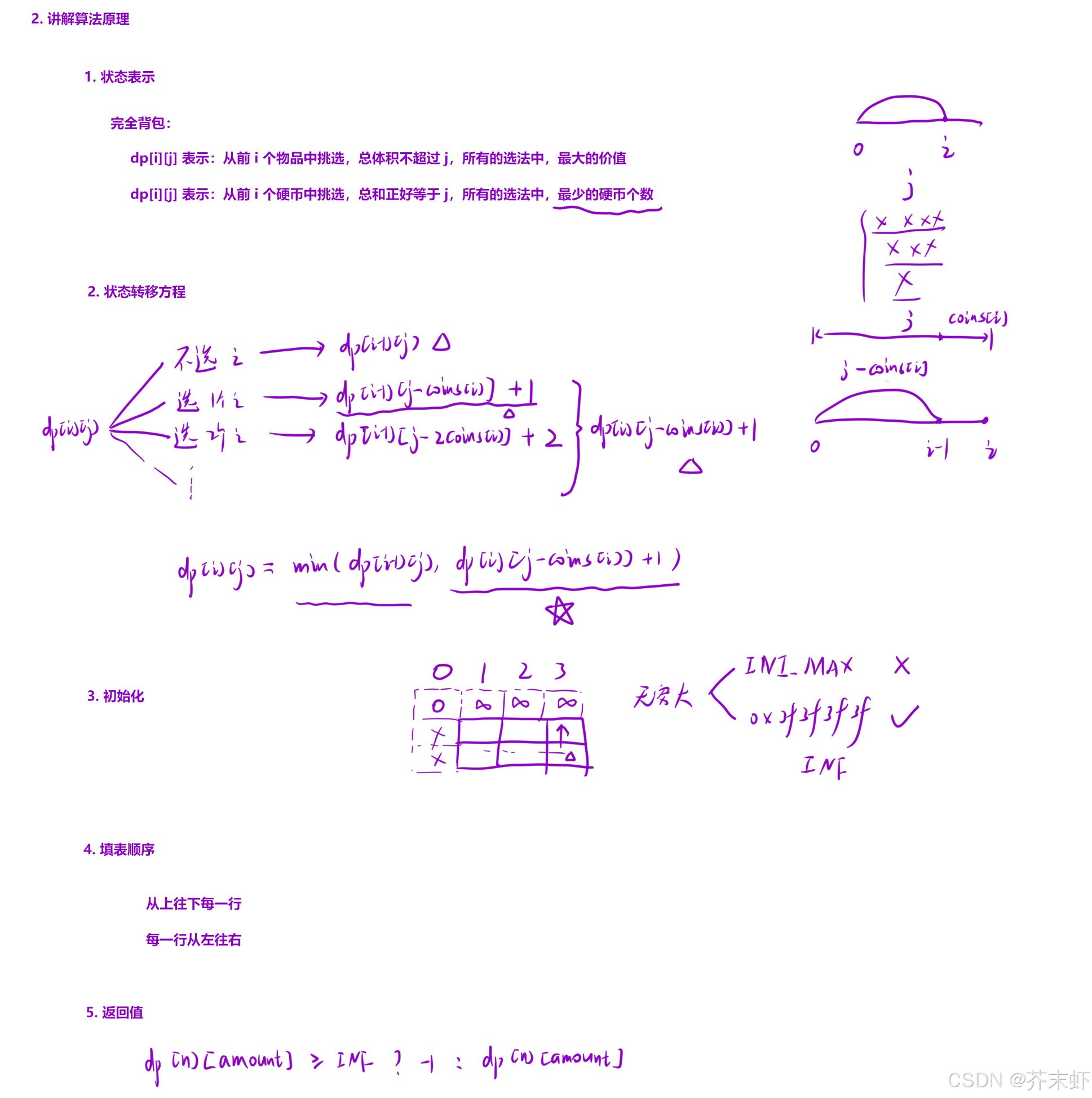
算法原理
提示:不能再像完全背包那样用-1表示无解。因为这里求的是最小值,如果使用-1,而不选i位置无解,即使选择i位置的零钱有解,也会在取min时取到-1。实际上我们设置无解为-1的初衷就是为了不参与后续的比较,因此可以用INF(无穷大)表示无解,这样的话,在取min时永远不会取到INF。
编写代码
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
const int INF = 0x3f3f3f3f;
int n = coins.size();
vector<vector<int>> dp(n+1, vector<int>(amount+1));
for(int j = 1; j <= amount; ++j)
dp[0][j] = INF;
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= amount; ++j)
{
dp[i][j] = dp[i-1][j];
if(j >= coins[i-1])
dp[i][j] = min(dp[i][j], dp[i][j-coins[i-1]]+1);
}
}
return dp[n][amount]>=INF? -1:dp[n][amount];
}
};
//空间优化
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
const int INF = 0x3f3f3f3f;
int n = coins.size();
vector<int> dp(amount+1);
for(int j = 1; j <= amount; ++j)
dp[j] = INF;
for(int i = 1; i <= n; ++i)
{
for(int j = coins[i-1]; j <= amount; ++j)
dp[j] = min(dp[j], dp[j-coins[i-1]]+1);
}
return dp[amount]>=INF? -1:dp[amount];
}
};
2.2.3 零钱兑换Ⅱ
题目链接
题目描述
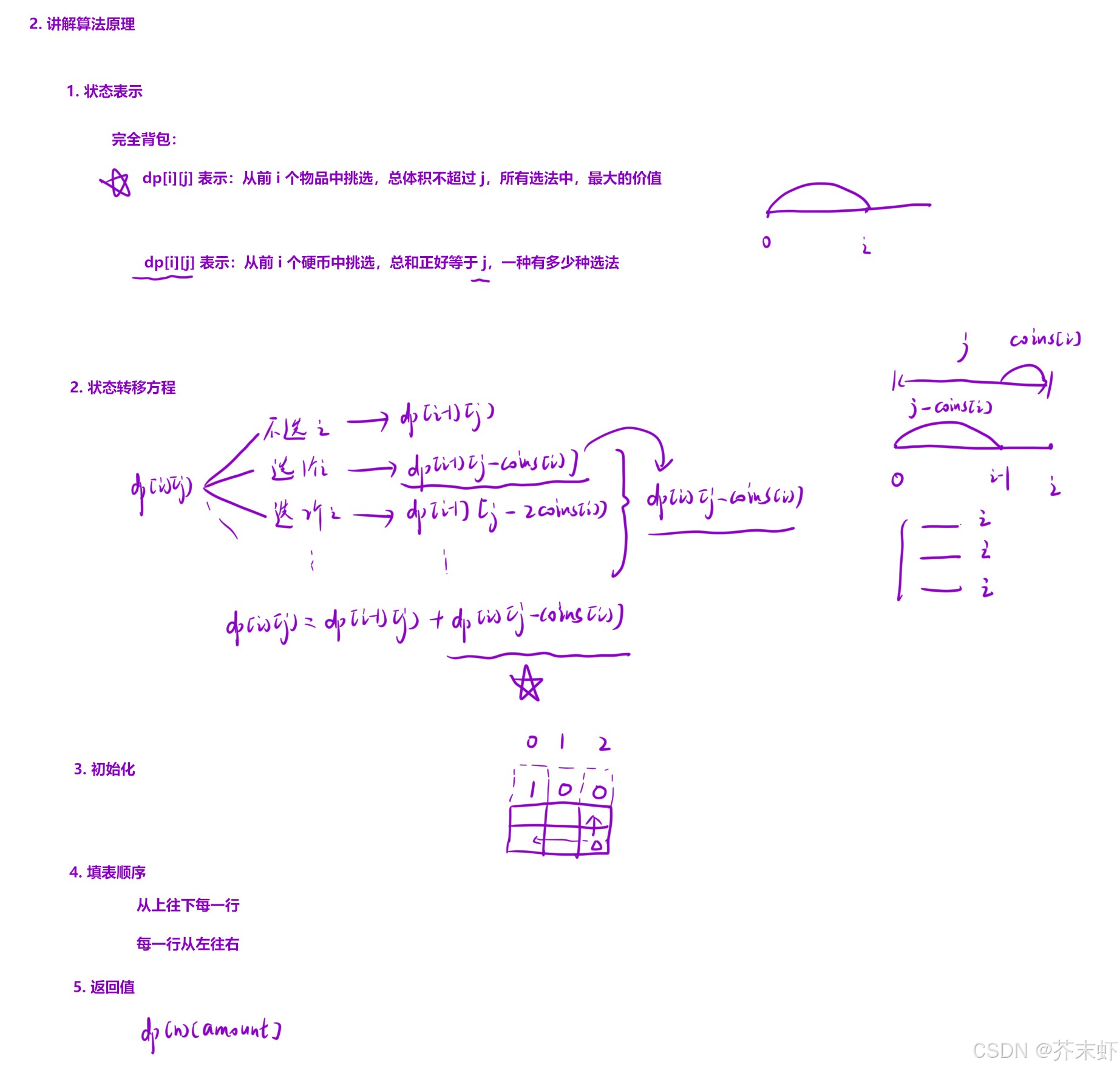
算法原理
编写代码
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n = coins.size();
vector<int> dp(amount+1);
dp[0] = 1;
for(auto e : coins)
{
for(int j = e; j <= amount; ++j)
dp[j]+=dp[j-e];
}
return dp[amount];
}
};
2.2.4 完全平方数
题目链接
题目描述
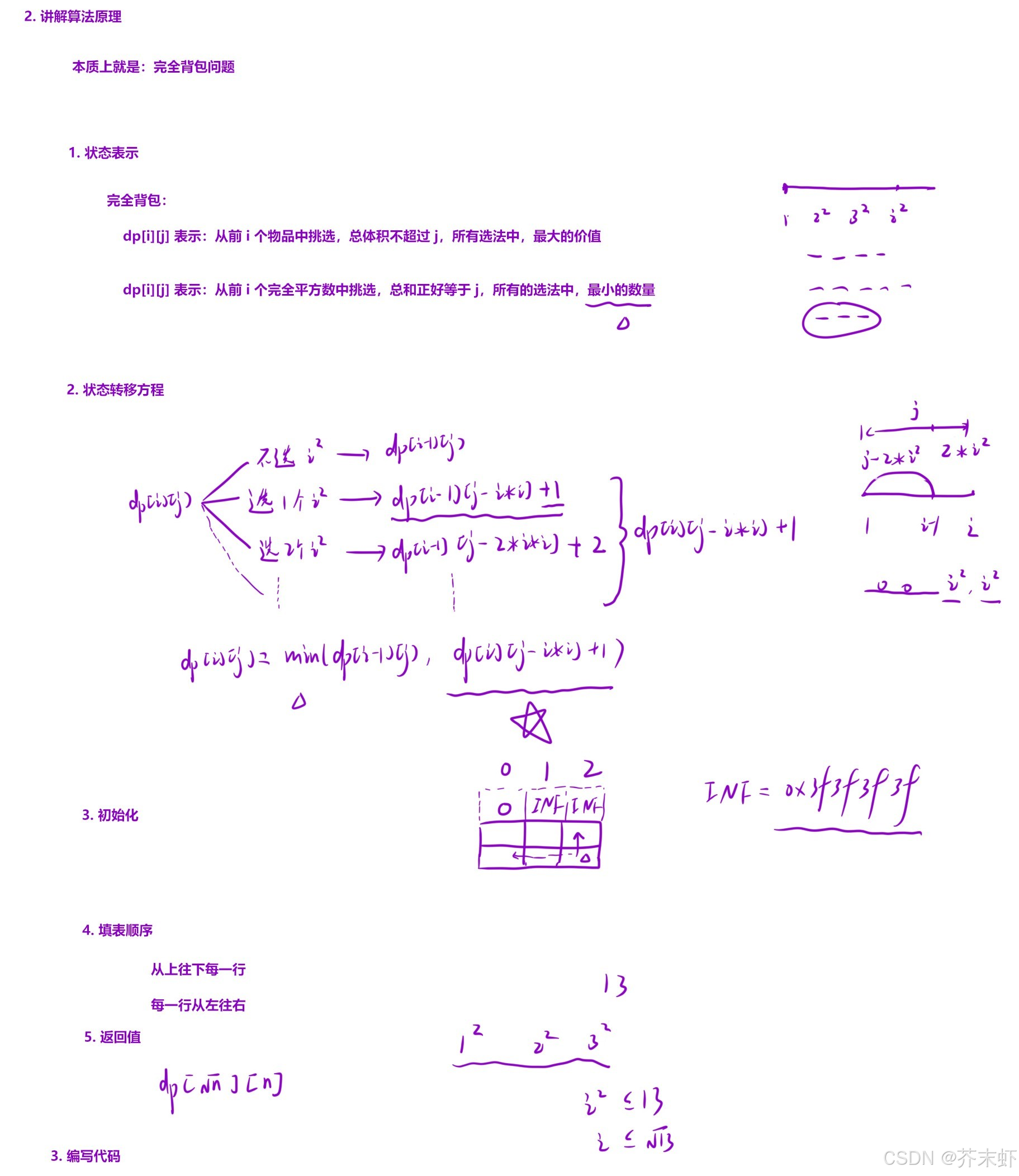
算法原理
编写代码
class Solution {
public:
int numSquares(int n) {
int m = sqrt(n);
const int INF = 0x3f3f3f3f;
vector<int> dp(n+1, INF);
dp[0] = 0;
for(int i = 1; i <= m; ++i)
{
for(int j = i*i; j <= n; ++j)
dp[j] = min(dp[j], dp[j-i*i]+1);
}
return dp[n];
}
};
2.3 二维费用背包问题
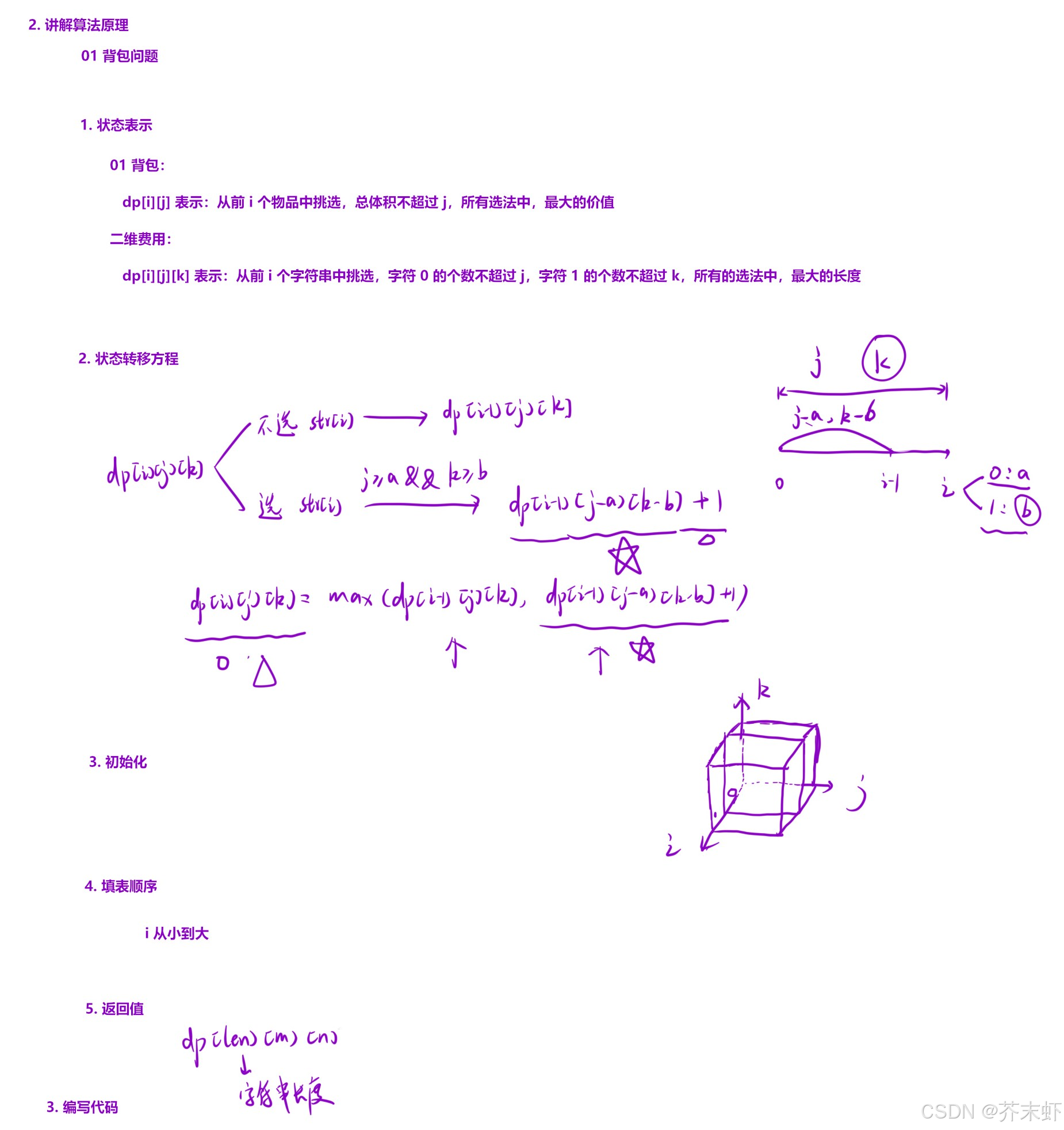
2.3.1 一和零
题目链接
题目描述
算法原理
- 01背包,不必装满,二维费用
编写代码
//三维dp表
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int cnt = strs.size();
vector<vector<vector<int>>> dp(cnt+1, vector<vector<int>>(m+1, vector<int>(n+1)));
for(int i = 1; i <= cnt; ++i)
{
//统计以下字符串中0,1的个数
int c0 = Count0(strs[i-1]);
int c1 = strs[i-1].size()-c0;
for(int j = 0; j <= m; ++j)
for(int k = 0; k <= n; ++k)
{
dp[i][j][k] = dp[i-1][j][k]; //不选i位置的字符串
if(j>=c0 && k>=c1) //选i位置的字符串
dp[i][j][k] = max(dp[i][j][k], dp[i-1][j-c0][k-c1]+1);
}
}
return dp[cnt][m][n];
}
int Count0(const string& str)
{
int cnt = 0;
for(auto ch : str)
if(ch == '0') ++cnt;
return cnt;
}
};
//空间优化:二维dp表
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int cnt = strs.size();
vector<vector<int>> dp(m+1, vector<int>(n+1));
for(int i = 1; i <= cnt; ++i)
{
int c0 = Count0(strs[i-1]);
int c1 = strs[i-1].size()-c0;
for(int j = m; j >= c0; --j) //注意从大到小遍历
for(int k = n; k >= c1; --k)
{
dp[j][k] = max(dp[j][k], dp[j-c0][k-c1]+1);
}
}
return dp[m][n];
}
};
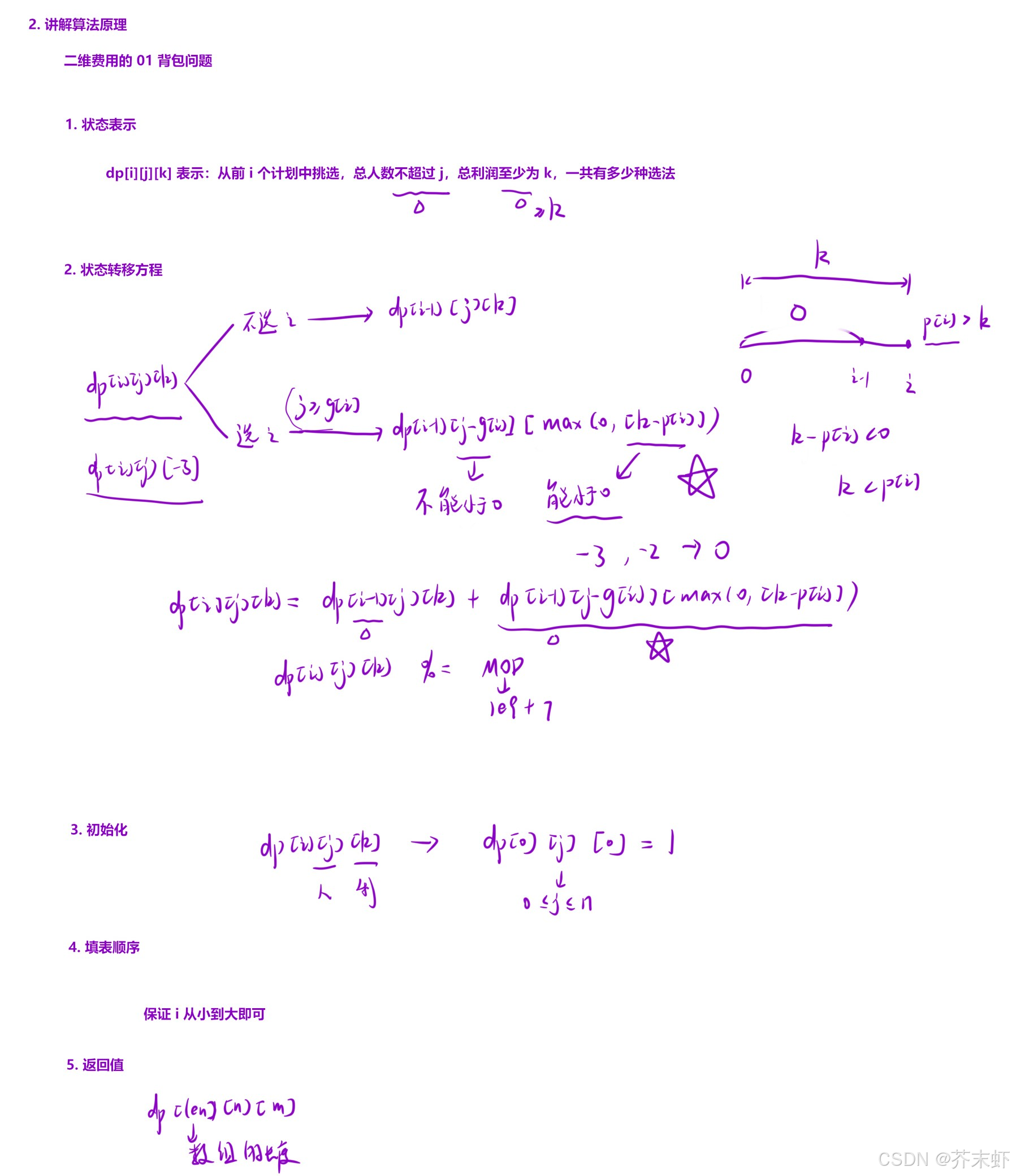
2.3.2 盈利计划
题目链接
题目描述
算法原理
提示:k可以小于p[i],表示单单i项计划的盈利就超过了最低限度k。但是作为数组的下标k-p[i]不能是负数,因此我们采取一个折中的方案,当k-p[i]<0时从前i-1项计划中选择的总利润最低为0即可。
编写代码
//三维dp表
class Solution {
public:
int profitableSchemes(int n, int m, vector<int>& group, vector<int>& profit) {
int cnt = group.size();
vector<vector<vector<int>>> dp(cnt+1, vector<vector<int>>(n+1, vector<int>(m+1)));
for(int j = 0; j <= n; ++j) dp[0][j][0] = 1; //没有计划,没有利润,无论多少人数都可以选空
for(int i = 1; i <= cnt; ++i)
{
for(int j = 0; j <= n; ++j)
{
for(int k = 0; k <= m; ++k)
{
dp[i][j][k] = dp[i-1][j][k];
if(j>=group[i-1])
dp[i][j][k] += dp[i-1][j-group[i-1]][max(0, k-profit[i-1])];
dp[i][j][k] %= (int)1e9+7;
}
}
}
return dp[cnt][n][m];
}
};
//空间优化:二维dp表
class Solution {
public:
int profitableSchemes(int n, int m, vector<int>& group, vector<int>& profit) {
int cnt = group.size();
vector<vector<int>> dp(n+1, vector<int>(m+1));
for(int j = 0; j <= n; ++j) dp[j][0] = 1;
for(int i = 1; i <= cnt; ++i)
{
for(int j = n; j >= group[i-1]; --j)
for(int k = m; k >= 0; --k)
{
dp[j][k] += dp[j-group[i-1]][max(0, k-profit[i-1])];
dp[j][k] %= (int)1e9+7;
}
}
return dp[n][m];
}
};