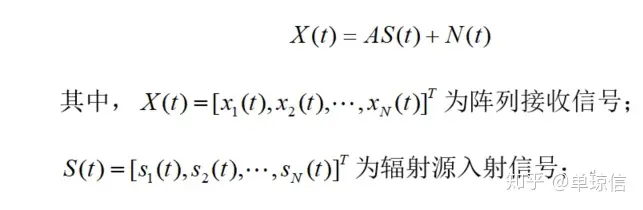本文转自知乎"单琼信"文章《1空间谱估计测向》，原文链接：https://zhuanlan.zhihu.com/p/160838685

有感于测向文档和实际仿真做的少的情况，总结一下基于MUSIC的DOA估计问题。(写公式太费劲了，直接截图~）

空间谱估计测向
具有多信号分辨能力的空间谱估计技术，有效的解决了同频多信号的测向问题，非常适用于频段十分拥挤的短波测向处理。主要应用于窄带测向，用于宽带测向的普遍做法是先进行信道化过程。主要有基于MUSIC和ESPRIT两大类算法，从测试情况来看，基于MUSIC的测向算法有更好的鲁棒性，因此超分辨测向主要采用MUSIC进行空间谱估计。

MUSIC测向原理
在阵列模型基础上，由于噪声与信号不相关，设空间有D个互不相关的信号，分别以方位角，，…，从远场入射到阵列中，可以认为信号到个天线阵元的方向角一致。如果入射信号的数目D小于阵列的阵元数N，则阵列的输出矢量为：

MUSIC实现总体方案

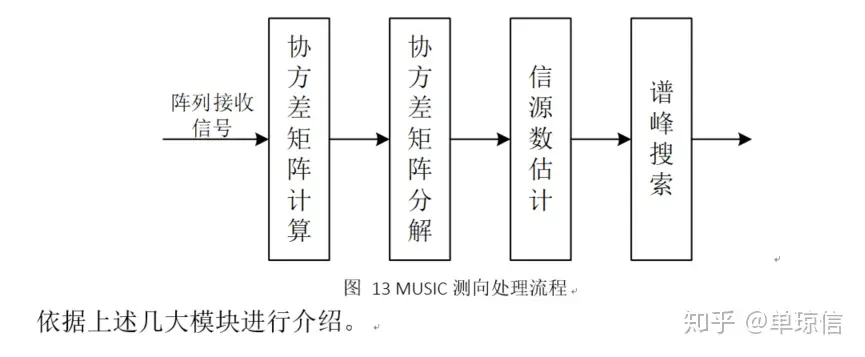
MUSIC测向的信号处理流程如下所示：

协方差矩阵计算

信号预处理

协方差计算

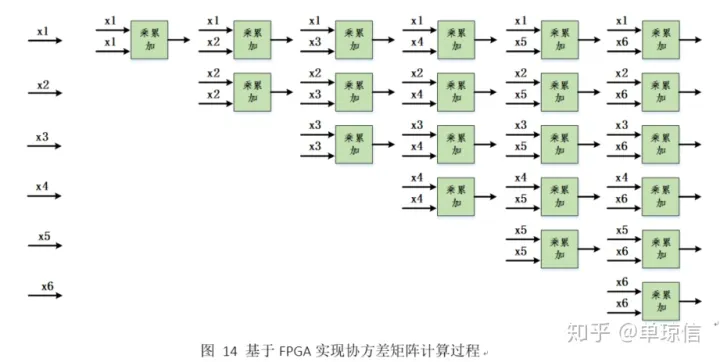
协方差矩阵的计算主要包括三个步骤：（1）调整阵元顺序；（2）对接收的阵列信号直接进行酉变换；（3）计算实数协方差矩阵R。

调整阵元顺序

阵列信号酉变换

协方差矩阵求解

协方差矩阵特征值分解

经典循环Jacobi过程

矩阵乘法元素计算

并行Jacobi变换实现过程

循环Jacobi方法采用了循环序列的方式作为平面旋转的序列排序方式，这是一种串行的序列排序方式，也是最常见的序列排序。但是这种循环排序的方式在旋转过程中，有强烈的数据以来关系，并不适合并行化计算。如以上述的行排序为例，再进行（1,2）旋转变换之后，会更新（1,2）两列矩阵元素，再进行（1,3）两列的旋转变换，其他的以此类推。这样就必须等待前面的序列旋转变换完成之后才可以进行下面的计算过程，无法实现算法的并行计算。

由于Jacobi算法中的平面旋转变换仅仅影响矩阵中的两行或两列的元素，因此如果可以合理排列旋转序列，就可以同时并行计算相互之间不影响的序列，从而提高算法的计算速度。

这里有几种数据交换序列的产生方式，主要有Caterpillar-Track序列、奇偶序列、Round-Robin序列以及指环序列（Ring ordering）。由于指环序列对矩阵特征分解的收敛速度起到积极作用。因此这里只对指环序列进行介绍。

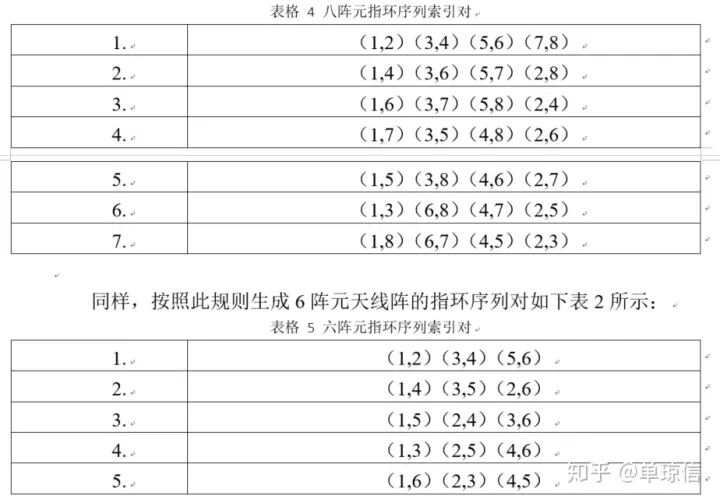
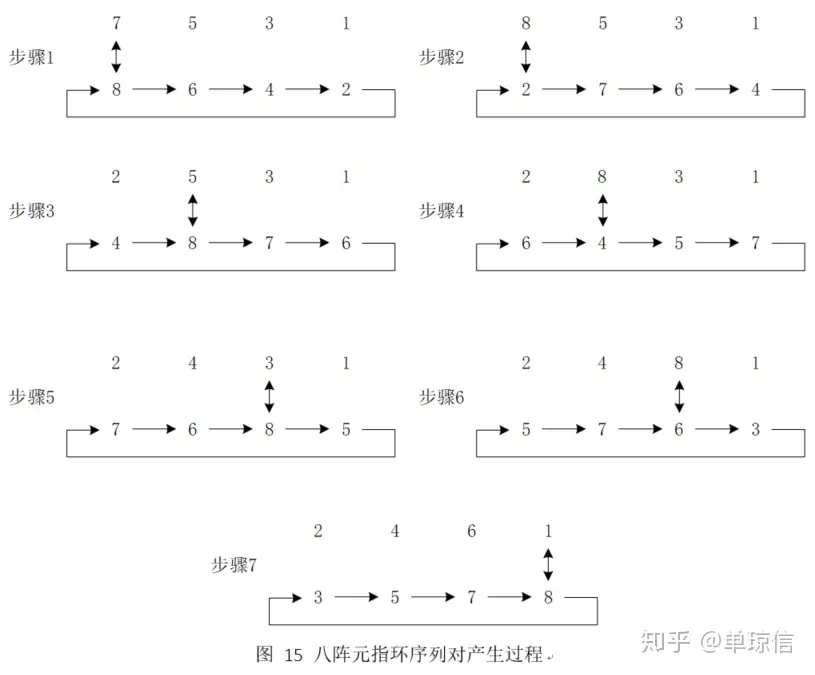
指环序列分为前向交换和后向交换两种，如下图是八阵元天线阵的前向交换指环序列产生过程，在任意一种指环序列中，n个索引被平均分为两行（因此这种序列更适合于偶数阵元的天线阵）。处于同一阶段同一列的两个索引构成一对。图4.3上下箭头表示在交换索引时，先将本列中的两个索引互换，然后再与其他列互换索引。整个过程需要n-1个阶段产生n(n-1)/2个索引对。因此针对8阵元天线，形成的索引对如下表所示:

信源估计

谱峰搜索

谱峰搜索实际上是进行乘累加，求內积之后，进行最大值或者最小值求解过程。（略）

% Function:     完成均匀圆阵DOA估计,完成对方位角的估计

clear
close all
clc

%% 设置 随机参数
rng('default');

%% signal paramter

M = 8;  % element number

% AOA in degree and transform to radi
AOA = [24,60];
a_phi = AOA*pi/180;
K = length(AOA);    % number of source
K =2;

f = [2000;2100];    % frequency for each source

fc=10e6; % Carrier frequency
c=3e8; % Speed of light (m/s)
lambda=c/fc; % wavelength
r = lambda/2;

% fs = 1;         % supposed sample rate as 1 
fs = 13.333e3;         % supposed sample rate as 1 


k_corr = 1;     %the fomer 'k_corr' sourcea are coherent,when =1 is uncorrelated

SNR =10;
aa = sqrt(SNR);%multipath coefficients

% n_array = 0:M-1;
% n_array = transpose(n_array);

gamma=2*pi*((0:M-1)./M); % Angle between two sensors (wrt origin and ref sensor)
gamma = transpose(gamma);
 
 
Lent = 512;
t = (0:Lent-1)./fs;  % number of sample or snapshots


%% signal generate


uu = exp(1i*2*pi*f*t);
% 4 style with filter
% 随机噪声通过滤波器产生叠加到原始信号
%rho = corrcoef(uu');% correlation cofficients

% B = exp(-1i*(2*pi*r/lambda)*cos(a_phi-gamma));

BB = exp(-1i*(2*pi*r/lambda)*cos(a_phi-gamma));
JJ1 = cat(2,diag(ones(M/2,1)),zeros(M/2));
JJ2 = cat(2,zeros(M/2),flipud(diag(ones(M/2,1))));
JJ = cat(1,JJ1,JJ2);
B = JJ*BB;

% d = lambda/2;
% n_array = 0:M-1;
% n_array = transpose(n_array);
% B = exp(-1i*2*pi*d*n_array*cos(a_phi)/lambda);%steer vector

T_signal=aa*B*uu;%the input signal


%% covariance matrix

noise = 0.1*(1i*randn(M,Lent)+randn(M,Lent))/sqrt(2);    %*sqrt(yita/2/K)
x = T_signal+noise;
R_con = x*x';

% rTT = flipud(eye(M));
rTT1 = cat(2,zeros(M/2),eye(M/2));
rTT2 = cat(2,eye(M/2), zeros(M/2));
rTT = cat(1,JJ1,JJ2);
% R_con1 = R_con - conj(R_con) + rTT*R_con*rTT - rTT*conj(R_con)*rTT ;
% R_con = R_con + rTT*conj(R_con)*rTT ;

%% DOA

thetat = (0:359)*pi/180;
% thetat = (0:180-1)*pi/180;
thetat_6p = repmat(thetat,[M,1]);

% [U,S,V]=svd(R_con);    
% Beta=U(:,K+1:M);
% a = exp(-1i*(2*pi*r/lambda)*cos(thetat_6p-gamma));
% Pmusic = sum(abs(Beta'*a).^2,1);

[Q,D]=eig(R_con); % Compute eigendecomposition of covariance matrix
Qn = Q(:,1:M-K);
% [Q1,~]=eig(R_con1); % Compute eigendecomposition of covariance matrix
% Qn1 = Q1(:,1:M-K);
% [Q2,~]=eig(R_con2); % Compute eigendecomposition of covariance matrix
% Qn2 = Q2(:,1:M-K);
% Qn = [Qn1,Qn2];
% a = exp(-1i*(2*pi*r/lambda)*cos(thetat_6p-gamma));
aa = exp(-1i*(2*pi*r/lambda)*cos(thetat_6p-gamma));
a = JJ*aa;
Pmusic = sum(abs(Qn'*a).^2,1);


figure,
grid on
hold on
plot(thetat/pi*180,10*log10(Pmusic),'r.-');
% plot(thetat/pi*180,Pmusic,'r.-');
xlabel('Angle:degree');
ylabel('Power dB');
legend('Pmusic')%'Pbw',


loc = find(diff(sign(diff(Pmusic))));   
[~,loc_ind] = sort(Pmusic(loc));
locate = loc(loc_ind(1:K));

disp(locate)


% Function:     并且采用复数相关矩阵转实数相关处理的预处理， 加入MDL信源个数估计

clear
close all
clc

%% 设置 随机参数
rng('default');

%% 偶数阵元

%=% signal paramter
M = 8;  % element number
% AOA in degree and transform to radi
AOA = [29,80];
a_phi = AOA*pi/180;
K = length(AOA);    % number of source
init_fai = rand(K,1)*pi;
% K =3;

Fs = 64e6;   
fc = 10e6;% Carrier frequency
f = fc+[2000;3e3];    % frequency for each source


 
c=3e8; % Speed of light (m/s)
lambda=c/fc; % wavelength
r = lambda/2;


gamma=2*pi*((0:M-1)./M); % Angle between two sensors (wrt origin and ref sensor)
gamma = transpose(gamma);


Lent = 512;
t = (0:Lent-1)./Fs;  % number of sample or snapshots

% signal generate
uu = exp(1i*2*pi*f*t+init_fai);
BB = exp(-1i*(2*pi*r/lambda)*cos(a_phi-gamma));
JJ1 = cat(2,diag(ones(M/2,1)),zeros(M/2));
JJ2 = cat(2,zeros(M/2),flipud(diag(ones(M/2,1))));
JJ = cat(1,JJ1,JJ2);
B = JJ*BB;

T_signal=B*uu;%the input signal
noise = (1i*randn(M,Lent)+randn(M,Lent))/sqrt(20);    %*sqrt(yita/2/K)
x = T_signal+noise;
 
%=% covariance matrix
diag1 = [ones(M/2,1);-1i*ones(M/2,1)];
diag2 = [1i*ones(M/2,1);ones(M/2,1)];
TT = diag(diag1) + flipud(diag(diag2));

TT = sqrt(1/2)*TT;  
xTT = TT*x;
R_con = real(xTT*xTT');

% ==========================================DOA=================================

% thetat = (0:359)*pi/180;
thetat = (0:0.1:360-0.1)*pi/180;
thetat_6p = repmat(thetat,[M,1]);

[Q,D]=eig(R_con); % Compute eigendecomposition of covariance matrix
[D,I]=sort(diag(D),1,'descend'); % Find s largest eigenvalues

% 信源个数估计 AIC
MDL = zeros(M,1);
for ds = 0:M-1
    mdl_tmp_d = D(ds+1:M);
    mdl_tmp1 = prod(mdl_tmp_d.^(1/(M-ds)));
    mdl_tmp2 = 1/(M-ds)*sum(mdl_tmp_d);
    MDL(ds+1) = -(M-ds)*Lent*log(mdl_tmp1/mdl_tmp2) + 1/2*ds*(2*M-ds)*log(Lent);
end

[~,K1] = min(MDL);
K1 = K1 -1;
disp(['K1 is ', num2str(K1)]);



Q=Q(:,I); % Sort the eigenvectors to put signal eigenvectors first
Qs=Q(:,1:K1); % Get the signal eigenvectors
Qn=Q(:,K1+1:M); % Get the noise eigenvectors

% aa = exp(-[kk*cos(thetat);kk*cos(thetat-pi/3);kk*cos(thetat-2*pi/3);...
%        kk*cos(thetat-5*pi/3);kk*cos(thetat-4*pi/3);kk*cos(thetat-pi)]);
aa = exp(-1i*(2*pi*r/lambda)*cos(thetat_6p-gamma));
a = TT*JJ*aa;

Pmusic = sum(abs(Qn'*a).^2, 1);


figure,
grid on
hold on
plot(thetat/pi*180,10*log10(Pmusic),'r.-');
% plot(thetat/pi*180,Pmusic,'r.-');
xlabel('Angle:degree');
ylabel('Power dB');
legend('Pmusic') %'Pbw',



loc = find(diff(sign(diff(Pmusic))));   
[~,loc_ind] = sort(Pmusic(loc));
locate = loc(loc_ind(1:K));

disp(locate/10)



% Function:     测试，推导双边jacobi的矩阵操作转成针对各个元素的操作是如何进行的

clear
clc
close all

%% 

N = 6;
% 构建实对称R矩阵
B = sym('R%d%d',[N,N]);
disp(B)


% 构建 Jacobi旋转因子，假定第一个点针对（1,2）
J = sym(eye(N));
J(1,1) = sym('c');
J(2,2) = sym('c');
J(2,1) = -sym('s');
J(1,2) = sym('s');
disp(J);


% Jacobi旋转
C = transpose(J)*B*J;
disp(C)


%对应的特征向量
UJ = sym(B);
UJ1 = UJ*J;
disp(UJ1);



Jacobi_two = sym('[c,s;-s,c]');
A = sym('[x,a+1i*b;a-1i*b,y]');
A1 = transpose(Jacobi_two)*A*Jacobi_two;
disp(A1);


% Function:     完成基于Jacobi的矩阵分解测试验证
% date 2019-05-26
%               这种测试是采用直接求解cos和sin的值，这种做法就需要采用求大量除法和根号来完成值的求解过程
% 
% date 2019-05-26
%               采用求解反正切的方法先求解出theta角，然后在求出对应的cos和sin,y
%               有问题，待验证，先采用直接求解法
% date 2019-05-27
%               采用按特定顺序完成一轮Jacobi变换，从而可以采用并行实现的方式完成一轮Jacobi变换
% 
% date 2019-05-29
%               之前是求正切的时候，使用了错的2倍tan值（论文提供的公式出错）
% 
% date 2019-05-29
%               将矩阵相乘操作分开成元素操作
%               对于6x6的实对称矩阵，如下：
%                 [ R11, R12, R13, R14, R15, R16]
%                 [ R21, R22, R23, R24, R25, R26]
%                 [ R31, R32, R33, R34, R35, R36]
%                 [ R41, R42, R43, R44, R45, R46]
%                 [ R51, R52, R53, R54, R55, R56]
%                 [ R61, R62, R63, R64, R65, R66]
% 针对上三角做运算，每一次旋转之后，对索引对（p,q)，该元素变为0，
% 对应的其他各个元素变化如下：
% Rpp = (Rpp*cos + Rpq*sin)*cos + (Rpq*cos + Rqq*sin)*sin
% Rqq = (Rqq*cos - Rpq*sin)*cos + (Rpq*cos - Rpp*sin)*sin


clear
clc

rng default

m = 6;
a = randn(m);
b = triu(a,0) + tril(a',-1);
B = b;

b1 = b;
disp('b is ')
disp(b)


UJ = eye(m);
UJ_tmp = UJ;
J_init = eye(m);

iteration = 10;
err = 1e-6;


%% 采用顺序遍历的方式完成一轮Jacobi变换

% 采用求反正切求角度，从而求解cos和sin值
for it = 1:iteration
    for p = 1:m
        for q= 1:m
            if (q > p)

                tan_double_theta = (2*b(p,q))/(b(q,q)-b(p,p));
                theta = 0.5*atan(tan_double_theta);
                c = cos(theta);
                s = sin(theta);
                
                B(p,p) = b(p,p)*c^2 - 2*b(p,q)*s*c + b(q,q)*s^2;
                B(q,q) = b(q,q)*c^2 + 2*b(p,q)*s*c + b(p,p)*s^2;
                for j = 1:m
                    if(j ~= p && j~=q)
                        B(p,j) = b(p,j)*c - b(q,j)*s;
                        B(j,p) = B(p,j);
                        B(q,j) = b(q,j)*c + b(p,j)*s;
                        B(j,q) = B(q,j);
                    end
                end
                B(p,q) = 0;
                B(q,p) = 0;
                b = B;
                
                    
                for i = 1:m
                    UJ_tmp(i,p) = UJ(i,p)*c - UJ(i,q)*s;
                    UJ_tmp(i,q) = UJ(i,q)*c + UJ(i,p)*s;
                end
                UJ = UJ_tmp;
%                 J = J_init;
%                 J(p,p) = c;
%                 J(q,q) = c;
%                 J(q,p) = -s;
%                 J(p,q) = s;
%                 UJ = UJ*J;
                
            end
        end
    end
    
end


% for it = 1:iteration
%     for i = 1:m
%         for j= 1:m
%             if (j > i)
% 
%                 tan_double_theta = (2*b(i,j))/(-b(i,i)+b(j,j));
%                 theta = 0.5*atan(tan_double_theta);
%                 c = cos(theta);
%                 s = sin(theta);
%                     
%                 J = J_init;
%                 J(i,i) = c;
%                 J(j,j) = c;
%                 J(j,i) = -s;
%                 J(i,j) = s;
% 
%                 b = transpose(J)*b*J;
%                 UJ = UJ*J;
% 
% 
%             end
%         end
%     end
%     
% end



%% 采用并行记录完成遍历

% % 当使用Round-Robing序列，m=6时，
% % （1,2），（3,4），（5,6）
% % （2,4），（1,5），（3,6）
% % （4,5），（2,3），（1,6）
% % （5,3），（4,1），（2,6）
% % （3,1），（5,2），（4,6）
% 
% % 指环序列索引对
% % （1,2），（3,4），（5,6）
% % （1,4），（3,5），（2,6）
% % （1,5），（2,4），（3,6）
% % （1,3），（2,5），（4,6）
% % （1,6），（2,3），（4,5）
% 
% % index = [1,2,3,4,5,6;...
% %          2,4,1,5,3,6;...
% %          4,5,2,3,1,6;...
% %          5,3,4,1,2,6;...
% %          3,1,5,2,4,6];
% 
% index = [1,2,3,4,5,6;...
%          1,4,3,5,2,6;...
%          1,5,2,4,3,6;...
%          1,3,2,5,4,6;...
%          1,6,2,3,4,5];
%    
% for it = 1:iteration
%     for ind = 1:m-1
%         i1 = index(ind,1);
%         j1 = index(ind,2);
%         i2 = index(ind,3);
%         j2 = index(ind,4);
%         i3 = index(ind,5);
%         j3 = index(ind,6);
%         
%         alpha1 = (b(j1,j1) - b(i1,i1))/(2*b(i1,j1));
%         tao1 = sign(alpha1)/(abs(alpha1) + sqrt(1+alpha1.^2));
%         c1 = 1/sqrt(1+tao1^2);
%         s1 = tao1*c1;     
%         J1 = J_init;
%         J1(i1,i1) = c1;
%         J1(j1,j1) = c1;
%         J1(j1,i1) = -s1;
%         J1(i1,j1) = s1;
%         
%         alpha2 = (b(j2,j2) - b(i2,i2))/(2*b(i2,j2));
%         tao2 = sign(alpha2)/(abs(alpha2) + sqrt(1+alpha2.^2));
%         c2 = 1/sqrt(1+tao2^2);
%         s2 = tao2*c2;
%         J2 = J_init;
%         J2(i2,i2) = c2;
%         J2(j2,j2) = c2;
%         J2(j2,i2) = -s2;
%         J2(i2,j2) = s2;
%         
%         alpha3 = (b(j3,j3) - b(i3,i3))/(2*b(i3,j3));
%         tao3 = sign(alpha3)/(abs(alpha3) + sqrt(1+alpha3.^2));
%         c3 = 1/sqrt(1+tao3^2);
%         s3 = tao3*c3;
%         J3 = J_init;
%         J3(i3,i3) = c3;
%         J3(j3,j3) = c3;
%         J3(j3,i3) = -s3;
%         J3(i3,j3) = s3; 
% 
%         b = transpose(J3)*(transpose(J2)*(transpose(J1)*b*J1)*J2)*J3;
%         UJ = UJ*J1*J2*J3;
% 
%     end
%     
% end



%% 显示结果

disp('after Jacobi, b is ');
disp(b)

disp('UJ is ');
disp(UJ);

bb = UJ*b*transpose(UJ);
% disp('bb is ')
% disp(bb)

disp('the difference is ');
disp(bb-b1);