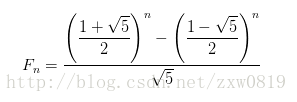f[1]=1; f[2]=2; f[n]=f[n-1]+f[n-2];
(1）递推

long long fib(int n)
{
    if(n==1) return 1;
    if(n==2) return 2;
    return fib(n-1)+fib(n-2);
}

(2) 循环

long long fib(int n)
{
    long long a=1,b=2,c;
    if(n==1) return 1;
    if(n==2) return 2;
    for(int i=3;i<=n;i++)
    {
        c=a+b;
        a=b;b=c;
    }
    return c;
}

（3）矩阵乘法（空间换时间）【可取模哦】

数列的递推公式由矩阵乘法表示为

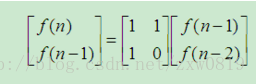
进一步，可得

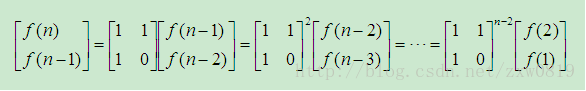
那我们如何计算

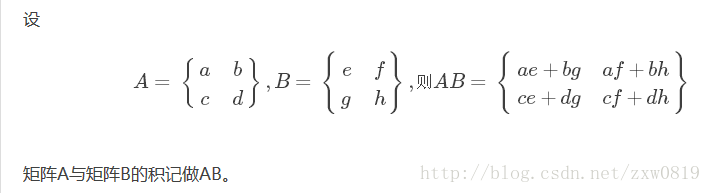
假设计算A的n次幂：
二阶矩阵的乘法满足结合律：A（BC）=（AB）C
法一：
令n=N/2;
1.若n为偶数，则A^N=A^n * A^n
2.若n为奇数，则A^N=A^n * A^n * A
举例：A^6=A^3 * A^3
A^7=A^3 * A^3 * A

//使用模板前需先分析f[2]=1还是2!!!!!!!!!!!!!!!!!!!!!(这里f[2]=1)
void multiply(int c[2][2],int a[2][2],int b[2][2],int mod)  
{  
    int tmp[4];  
    tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];  
    tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];  
    tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0];  
    tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1];  
    c[0][0]=tmp[0]%mod;  
    c[0][1]=tmp[1]%mod;  
    c[1][0]=tmp[2]%mod;  
    c[1][1]=tmp[3]%mod;  
}//计算矩阵乘法，c=a*b  

int fibonacci(int n,int mod)//mod表示数字太大时需要模的数  
{  
    if(n==0)return 0;  
    else if(n<=2)return 1;//这里表示第0项为0，第1，2项为1  

    int a[2][2]={{1,1},{1,0}};  
    int result[2][2]={{1,0},{0,1}};//初始化为单位矩阵  
    int s;  
    n-=2;  
    while(n>0)  
    {  
        if(n%2 == 1)  
            multiply(result,result,a,mod);  
        multiply(a,a,a,mod);  
        n /= 2;  
    }//二分法求矩阵幂  
    s=(result[0][0]+result[0][1])%mod;//结果  
    return s;  
}  

法二：
“二进位为1需要乘，为0不需要乘”
以计算A^6为例：
A^6=A^4 * A^2
将6转换成二进制：110
第2位为1，需要乘，乘2^2（即A^4）; 第1位还为1，需要乘，乘2^1(即A^2); 第0位为0，不需要乘。
即：若需要乘，则乘2^pos.
十进制7 = 二进制 111
则A^7=A^4∗A^2∗A^1

////使用模板前需先分析f[2]=1还是2!!!!!!!!!!!!!!!!!!!!!(这里f[2]=2)
///求解fac(n)%100000，其中n为大于等于3的正整数
#include<stdio.h>
#include<math.h>
long long fac_tmp[6][4]={   ///存放矩阵次幂
                    ///位置：00 01 10 11
                   {24578,78309,78309,46269},   ///32次幂%100000
                   {1597,987,987,610},  ///16次幂%100000
                   {34,21,21,13},   ///8次幂%100000
                   {5,3,3,2},   ///4次幂%100000
                   {2,1,1,1},   ///2次幂%100000
                   {1,1,1,0},   ///1次幂%100000
                   };
void fac(int);

int main()
{
    int n;
    scanf("%d",&n);
    fac(n);
    return 1;
}

void fac(int k) ///k>=3
{
    int i;
    long long t00=1,t01=1,t10=1,t11=0;  ///表示矩阵的1次幂
    long long a,b,c,d;
    k=k-3;  ///公式中是n-2次幂，(t00,t01,t10,t11)表示1次幂。所以一共减3次
    for(i=k;i>=32;i=i-32)   ///对于大于等于32的k;
    {
        a=(t00*fac_tmp[0][0]+t01*fac_tmp[0][2])%100000;
        b=(t00*fac_tmp[0][1]+t01*fac_tmp[0][3])%100000;
        c=(t10*fac_tmp[0][0]+t11*fac_tmp[0][2])%100000;
        d=(t10*fac_tmp[0][1]+t11*fac_tmp[0][3])%100000;
        t00=a;  t01=b;  t10=c;t11=d;
    }

    i=4;
    while(i>=0)    ///对于小于32的k(16,8,4,2,1);
    {
        if(k>=(long long)pow(2,i))  ///如果k大于某一个2的次幂
        {

            a=(t00*fac_tmp[5-i][0]+t01*fac_tmp[5-i][2])%100000; ///(5-i)：矩阵的2的i次幂在数组fac_tmp中的位置为fac_tmp[5-i]
            b=(t00*fac_tmp[5-i][1]+t01*fac_tmp[5-i][3])%100000;
            c=(t10*fac_tmp[5-i][0]+t11*fac_tmp[5-i][2])%100000;
            d=(t10*fac_tmp[5-i][1]+t11*fac_tmp[5-i][3])%100000;
            t00=a;  t01=b;  t10=c;t11=d;
            k=k-(int)pow(2,i);
        }
        i--;
    }

    a=(t00*2+t01*1)%100000;
    printf("%lld\n",a);
}

(4) 直接上公式……