C 语言函数：数字江湖的秘籍要诀与侠义传功

一、函数的概念

数学中我们常见到函数的概念。

但是你了解C语言中的函数吗？

维基百科中对函数的定义： 子程序

在计算机科学中，子程序（英语：Subroutine, procedure, function, routine, method, subprogram, callable unit），是一个大型程序中的某部分代码，由一个或多个语句块组成。它负责完成某项特定任务，而且相较于其他代码，具备相对的独立性。
一般会有输入参数并有返回值，提供对过程的封装和细节的隐藏。这些代码通常被集成为软件库。

二、C语言中函数的分类

1. 库函数

（1）为什么会有库函数？

我们知道在我们学习C语言编程的时候，总是在一个代码编写完成之后迫不及待的想知道结果，想把这个结果打印到我们的屏幕上看看。这个时候我们会频繁的使用一个功能：将信息按照一定的格式打印到屏幕上（printf）。
在编程的过程中我们会频繁的做一些字符串的拷贝工作（strcpy）。
在编程是我们也计算，总是会计算n的k次方这样的运算（pow）。

像上面我们描述的基础功能，它们不是业务性的代码。我们在开发的过程中每个程序员都可能用的到， 为了支持可移植性和提高程序的效率，所以C语言的基础库中提供了一系列类似的库函数，方便程序员进行软件开发。

那怎么学习库函数呢？

这里我们简单的看看：http:// www.cplusplus.com

简单的总结，C语言常用的库函数都有：

IO函数
字符串操作函数
字符操作函数
内存操作函数
时间/日期函数
数学函数
其他库函数

（2）学习几个库函数

sqrt
double sqrt (double x);
//sqrt 是函数名 
//x 是函数的参数，表⽰调⽤sqrt函数需要传递⼀个double类型的值 
//double 是返回值类型 - 表⽰函数计算的结果是double类型的值 
功能

Compute square root 计算平⽅根

Returns the square roo to fx.（返回平⽅根）

头文件包含

库函数是在标准库中对应的头⽂件中声明的，所以库函数的使⽤，务必包含对应的头⽂件，不包含是可能会出现⼀些问题的。<math.h>

例子
/* sqrt example */
#include <stdio.h>      /* printf */
#include <math.h>       /* sqrt */

int main ()
{
  double param, result;
  param = 1024.0;
  result = sqrt (param);
  printf ("sqrt(%f) = %f\n", param, result );
  return 0;
strcpy

功能

Copy string

Copies the C string pointed by source into the array pointed by destination, including the terminating null character (and stopping at that point).
To avoid overflows, the size of the array pointed by destination shall be long enough to contain the same C string as source (including the terminating null character), and should not overlap in memory with source.

头文件包含

<string.h>

例子
/* strcpy example */
#include <stdio.h>
#include <string.h>

int main ()
{
  char str1[]="Sample string";
  char str2[40];
  char str3[40];
  strcpy (str2,str1);
  strcpy (str3,"copy successful");
  printf ("str1: %s\nstr2: %s\nstr3: %s\n",str1,str2,str3);
  return 0;
}
memset

功能

Fill block of memory

Sets the first num bytes of the block of memory pointed by ptr to the specified value (interpreted as an unsigned char).

头文件包含

<string.h>

例子
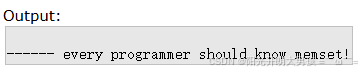
/* memset example */
#include <stdio.h>
#include <string.h>

int main ()
{
  char str[] = "almost every programmer should know memset!";
  memset (str,'-',6);
  puts (str);
  return 0;
}
（3）如何学会使用库函数？

需要全部记住吗？No

需要学会查询工具的使用：

MSDN(Microsoft Developer Network)
www.cplusplus.com
http://en.cppreference.com（英文版）
http://zh.cppreference.com（中文版）

英文很重要。最起码得看懂文献。

2.自定义函数

如果库函数能干所有的事情，那还要程序员干什么？

所以更加重要的是自定义函数。

自定义函数和库函数一样，有函数名，返回值类型和函数参数。

但是不一样的是这些都是我们自己来设计。

这给程序员一个很大的发挥空间。

（1）函数的组成：
ret_type fun_name(para1, * )
 {
     statement;//语句项
}
ret_type 返回类型
fun_name 函数名
para1 函数参数
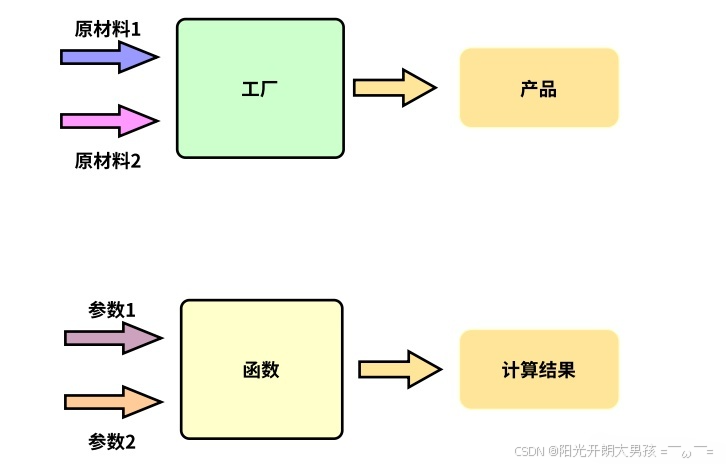
{}括起来的 statement; 是函数体

在编程领域，函数好似小型加工厂。工厂需输入原材料以产出产品，函数亦接收值（可为 0 个或多个）作为 “原材料”，经内部 “加工” 得出结果。

返回类型 ret_type 如工厂产出物的类型界定，void 类似无实际产品输出的流程。

函数名 fun_name 是工厂招牌，依功能而取的恰当名字，像 “encryptFile”，便于识别调用，提升代码可读性。

函数参数 para1 仿若进厂原材料，可为 void 即无输入，有参数时需明确定义其类型、名称与数量，以供函数精准运作。

{} 括起的函数体则是核心加工区，依逻辑处理参数，将其转化为最终 “产品”—— 返回值。

（2）函数举例

找出两个整数中的最大值
#include <stdio.h>
//get_max函数的设计
int get_max(int x, int y)
{
    return (x>y)?(x):(y);
}
int main()
{
    int num1 = 10;
    int num2 = 20;
    int max = get_max(num1, num2);
    printf("max = %d\n", max);
    return 0;
}
交换两个整形变量

错误的尝试
#include <stdio.h>
//实现成函数，但是不能完成任务
void Swap1(int x, int y)
{
    int tmp = 0;
    tmp = x;
    x = y;
    y = tmp;
}
表面操作：
从代码表面看，在 Swap1 函数内部，定义了临时变量 tmp，并通过三步操作，先是将 x 的值赋给 tmp，接着把 y 的值赋给 x，最后把 tmp（原本 x 的值）赋给 y，看似完成了 x 和 y 两个变量值的交换。
实际问题：
这里的 x 和 y 属于函数内部的形式参数。
形式参数只有在函数被调用过程中才实例化（分配内存单元），当函数调用结束后，它们就会自动销毁。
所以，虽然在函数内部对它们的值进行了互换操作，但这种改变并不会作用到函数外部传入的实际变量上，也就无法真正实现交换两个外部变量值的目的。

正确的做法（这里使用指针解决以上问题）
#include <stdio.h>
//正确的版本
void Swap2(int *px, int *py)
{
    int tmp = 0;
    tmp = *px;
    *px = *py;
    *py = tmp;
}
int main()
{
    int num1 = 1;
    int num2 = 2;
    Swap1(num1, num2);
    printf("Swap1::num1 = %d num2 = %d\n", num1, num2);
    Swap2(&num1, &num2);
    printf("Swap2::num1 = %d num2 = %d\n", num1, num2);
    return 0;
}
函数定义思路：
Swap2 函数的参数 px 和 py 定义为指向整数的指针类型。
通过指针操作，在函数内部借助临时变量 tmp，先将 *px（即所指向的外部实际变量的值）保存起来，然后把 *py 的值赋给 *px，再把之前保存的 *px 的值赋给 *py，从而实现对外部实际变量值的交换。

三、函数的参数

1. 实际参数（实参）

真实传给函数的参数，叫实参。

实参可以是：常量、变量、表达式、函数等。

无论实参是何种类型的量，在进行函数调用时，它们都必须有确定的值，以便把这些值传送给形参。

在main函数中传给 Swap1 的 num1 ，和 num2 传给Swap2 函数的 &num1 ， &num2 是实际参数。

2.形式参数（形参）

形式参数是指函数名后括号中的变量，因为形式参数只有在函数被调用的过程中才实例化（分配内存单元），所以叫形式参数。形式参数当函数调用完成之后就自动销毁了。因此形式参数只在函数中有效。

上面Swap1和 Swap2 函数中的参数 x，y，px，py都是形式参数。

3.实参和形参的关系

我们可以理解为形参是实参的⼀份临时拷⻉。

这里我们对函数的实参和形参进行分析：

这里可以看到 Swap1 函数在调用的时候，x，y拥有自己的空间，同时拥有了和实参一模一样的内容。

四、函数的调用

1.传值调用

函数的形参和实参分别占有不同内存块，对形参的修改不会影响实参。

简单来说，就是在函数内部对形参进行的任何修改，都不会影响到实参原本的值。

例如：
#include <stdio.h>

void modifyValue(int x) {
    x = 10;  // 在函数内修改形参 x 的值
}

int main() {
    int num = 5;
    modifyValue(num);
    printf("num 的值依然是: %d\n", num);  // 输出 num 的值，会发现还是 5，并没有被函数内的修改影响
    return 0;
}
2.传址调用

传址调用是把函数外部创建变量的内存地址传递给函数参数的一种调用函数的方式。
这种传参方式可以让函数和函数外边的变量建立起真正的联系，也就是函数内部可以直接操作函数外部的变量

例如：
#include <stdio.h>

void swap(int *a, int *b) {
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}

int main() {
    int num1 = 3, num2 = 5;
    swap(&num1, &num2);
    printf("交换后 num1 的值为: %d，num2 的值为: %d\n", num1, num2);
    return 0;
}
3.实战演练

（1）判断一个数是不是素数

素数是指在大于 1 的自然数中，除了 1 和它自身外，不能被其他自然数整除的数。下面是一个判断素数的函数示例：
#include <stdio.h>
#include <math.h>

int isPrime(int n) {
    if (n < 2) {
        return 0;
    }
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) {
            return 0;
        }
    }
    return 1;
}

int main() {
    int num;
    printf("请输入一个整数: ");
    scanf("%d", &num);
    if (isPrime(num)) {
        printf("%d 是素数\n", num);
    } else {
        printf("%d 不是素数\n", num);
    }
    return 0;
}
（2）判断一年是不是闰年

四年一闰，百年不润，四百年再闰一次
#include <stdio.h>

int isLeapYear(int year) {
    return (year % 4 == 0 && year % 100!= 0) || (year % 400 == 0);
}

int main() {
    int year;
    printf("请输入一个年份: ");
    scanf("%d", &year);
    if (isLeapYear(year)) {
        printf("%d 年是闰年\n", year);
    } else {
        printf("%d 年不是闰年\n", year);
    }
    return 0;
}
（3）每调用一次函数，使变量值增加 1
#include <stdio.h>

void increment(int *num) {
    (*num)++;
}

int main() {
    int num = 0;
    increment(&num);
    printf("第一次调用后 num 的值为: %d\n", num);
    increment(&num);
    printf("第二次调用后 num 的值为: %d\n", num);
    return 0;
}

五、函数的嵌套调用和链式访问

函数和函数之间可以根据实际的需求进行组合的，也就是互相调用的。

1. 嵌套调用

嵌套调⽤就是函数之间的互相调⽤

例如：
#include <stdio.h>
 void new_line()
 {
     printf("hehe\n");
 }
 void three_line()
 {
     int i = 0;
     for(i=0; i<3; i++)
    {
         new_line();
    }
 }
 int main()
 {
    three_line();
    return 0;
 }
注意：函数可以嵌套调用，但是不能嵌套定义。

2. 链式访问

把一个函数的返回值作为另外一个函数的参数。

例如:
#include <stdio.h>
 int main()
 {
     printf("%d", printf("%d", printf("%d", 43)));
//结果是啥？
//注：printf函数的返回值是打印在屏幕上字符的个数
    return 0;
 }
最内层 printf 执行

最内层的 printf("%d", 43) 率先运行。其功能为在屏幕上输出数字 43。
依据 printf 函数返回值为打印字符个数的规则，这里输出了 2 个字符（即 43），所以该内层 printf 的返回值为 2。

中间层 printf 执行

中间层的 printf("%d", printf("%d", 43)) 开始工作。由于内层已返回 2，此时它相当于执行 printf("%d", 2)。
这会在屏幕上接着打印出数字 2，且此次仅打印了 1 个字符，所以该中间层 printf 的返回值为 1。

最外层 printf 执行

最外层的 printf("%d", printf("%d", printf("%d", 43))) 最后执行。鉴于中间层返回了 1，它等同于执行 printf("%d", 1)。
于是在屏幕上再打印出数字 1。

六、函数的声明和定义

1. 函数声明

告诉编译器有一个函数叫什么，参数是什么，返回类型是什么。但是具体是不是存在，函数声明决定不了。
函数的声明一般出现在函数的使用之前。要满足先声明后使用。
函数的声明一般要放在头文件中的。

一般的函数写法：
#include <stdio.h>
//get_max函数的设计
int get_max(int x, int y)
{
	return (x > y) ? (x) : (y);
}
int main()
{
	int num1 = 10;
	int num2 = 20;
	int max = get_max(num1, num2);
	printf("max = %d\n", max);
	return 0;
}
如果想把函数放在 main 函数下面，需要在 main 函数上面写函数声明，否则会报错

例如：
#include <stdio.h>
//get_max函数的设计
int get_max(int x, int y);

int main()
{
	int num1 = 10;
	int num2 = 20;
	int max = get_max(num1, num2);
	printf("max = %d\n", max);
	return 0;
}

int get_max(int x, int y)
{
	return (x > y) ? (x) : (y);
}
函数的调⽤⼀定要满⾜，先声明后使⽤。

2. 函数定义（多文件）

函数的定义是指函数的具体实现，交待函数的功能实现。

在企业 C 语言编程中，因项目代码量大，不会将所有代码置于单文件。而是依程序功能拆分代码至多个文件。

头文件（.h）存放函数声明、类型声明与库函数所需头文件包含语句，如数学模块头文件可声明函数接口、引入库并自定义类型。它如同代码 “说明书”，明确模块信息。

add.h
#include <stdio.h>
//函数的声明 
int Add(int x, int y);
源文件（.c）负责实现头文件中声明的函数功能。像数学模块的源文件会具体定义函数运算逻辑。

add.c
#include "add.h"
//函数的定义 
int Add(int x, int y)
{
    return x+y;
}
test.c（测试）
#include "add.h"
int main()
{
    int a = 10;
    int b = 20;
    //函数调⽤ 
    int c = Add(a, b);
    printf("%d\n", c);
    return 0;
}

七、函数递归

1. 什么是递归？

（1）递归的概念

程序调用自身的编程技巧称为递归（ recursion）。

递归做为一种算法在程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

递归的主要思考方式在于：把大事化小

（2）递归的两个必要条件

存在限制条件，当满足这个限制条件的时候，递归便不再继续。
每次递归调用之后越来越接近这个限制条件。

2.递归举例

（1）求n的阶乘

⼀个正整数的阶乘（factorial）是所有⼩于及等于该数的正整数的积，并且0的阶乘为1。⾃然数n的阶乘写作n!。

阶乘的公式：n！ = n ∗ (n − 1)!
当 n==0 的时候，n的阶乘是1，其余n的阶乘都是可以通过公式计算。

函数如下：
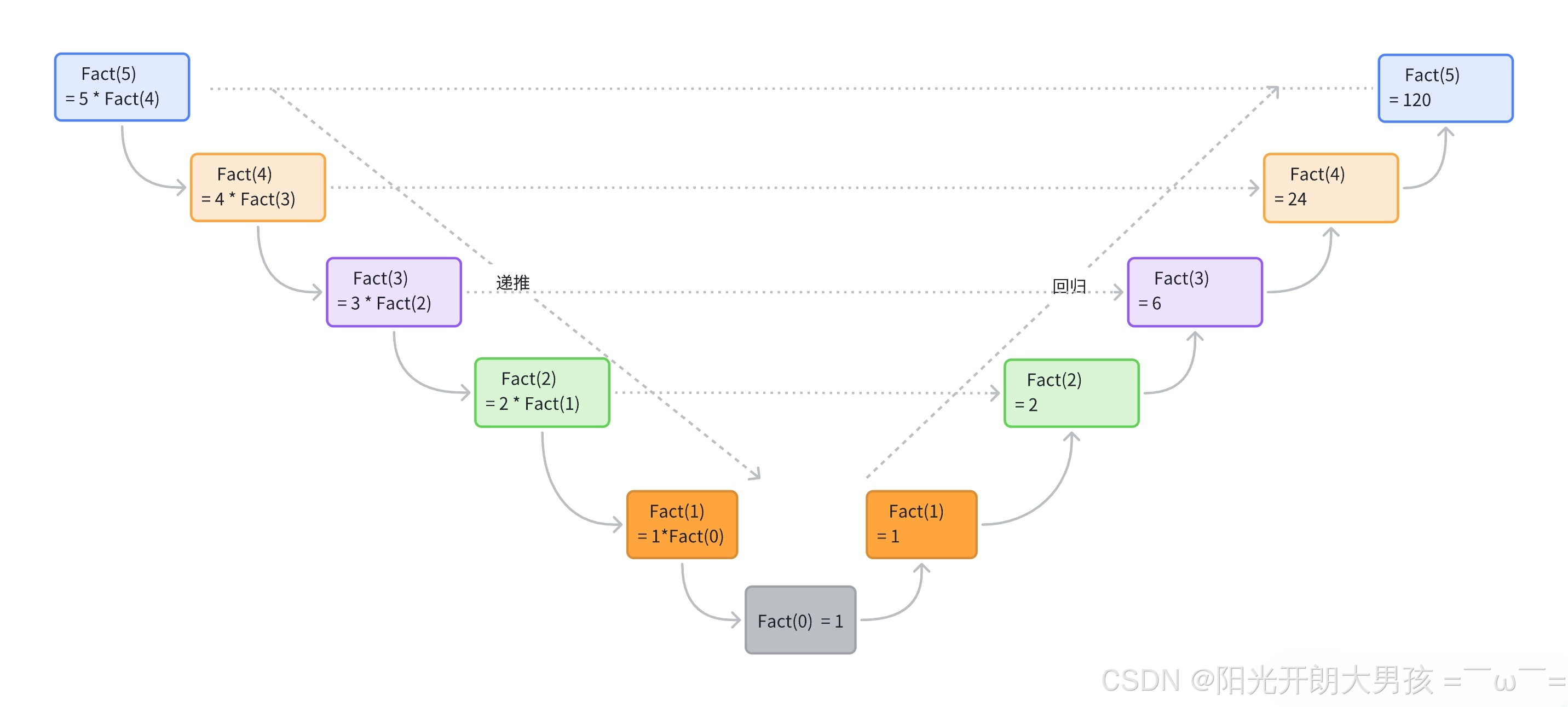
int Fact(int n)
{
    if(n==0)
        return 1;
    else
        return n*Fact(n-1);
}
图例：

（2）顺序打印一个整数的每一位

接受一个整型值（无符号），按照顺序打印它的每一位。

例如：输入：1234，输出 1 2 3 4.

解决思路剖析

关键发现：数字的最低位易通过 %10 得到。
函数拆分示例：以 Print (1234) 为例。
首先进行 Print (1234/10)，即先处理 123 的每一位打印，此为将大问题转化为子问题，践行 “大事化小” 思路。
接着打印 1234%10 得到的 4。如此，两步完成 1234 每一位打印。同理，Print (123) 可拆分为 Print (12) 与打印 3 等步骤，直至数字为一位数。

函数如下：
void Print(int n)
{
    if(n>9)
    {
        Print(n/10); // 若 n 大于 9，先递归处理更高位数字
    }
    printf("%d ", n%10); // 打印当前数字最低位
}
图例：

3.递归与迭代

（1）递归的优缺点

递归的双面性

优势魅力：递归以简洁代码处理复杂任务，如应对树结构与数学算法，富有逻辑美感。
误用风险：易被滥用，像求阶乘时，常因公式直观而写成递归形式，却可能忽视后续问题。

递归的运行代价

栈帧空间占用：C 语言中每次函数调用，于内存栈区开辟函数栈帧存局部变量。
递归时的隐患：递归调用时，每层递归均新开栈帧且不返回就不释放。一旦递归过深，大量栈帧累积，造成空间浪费，甚至引发栈溢出（stackoverflow）致程序崩溃。

迭代：递归的替代之选

原理与特性：采用循环的迭代方式，不依赖多层函数调用与栈帧开辟。
优势与适用场景：高效利用资源，适合内存敏感或递归深度难测场景，保障程序稳定高效运行，避免递归潜在风险。

（2）递归与迭代的对比

递归求第n个斐波那契数

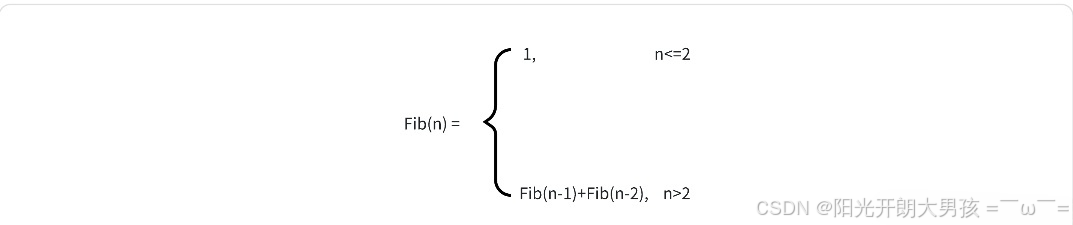
递归函数：
int Fib(int n)
{
    if(n<=2)
        return 1;
    else
        return Fib(n-1)+Fib(n-2);
}
图例：

但是我们发现有问题：

使用Fib这个函数的时候如果我们要计算第50个斐波那契数字的时候特别耗费时间。
使用 Fib 函数求10000的阶乘（不考虑结果的正确性），程序会崩溃。

为什么呢？

我们发现fib函数在调用的过程中很多计算其实在一直重复。如果我们把代码修改一下：
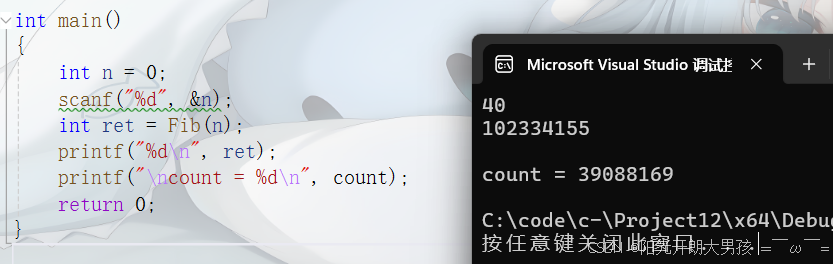
#include <stdio.h>

int count = 0;
int Fib(int n)
{
    if(n == 3)
        count++;//统计第3个斐波那契数被计算的次数 
    if(n<=2)
        return 1;
    else
        return Fib(n-1)+Fib(n-2);
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    int ret = Fib(n);
    printf("%d\n", ret); 
    printf("\ncount = %d\n", count);
    return 0;
}
在计算第40个斐波那契数的时候，使⽤递归⽅式，第3个斐波那契数就被重复计算了 39088169次，这些计算是⾮常冗余的。

那如何解决上述的问题：

将递归改写成非递归。
使用 static 对象替代 nonstatic 局部对象。在递归函数设计中，可以使用 static 对象替代 nonstatic 局部对象（即栈对象），这不仅可以减少每次递归调用和返回时产生和释放 nonstatic 对象的开销，而且 static 对象还可以保存递归调用的中间状态，并且可为各个调用层所访问。

所以斐波那契数的计算，使⽤递归是⾮常不明智的，我们试试迭代的⽅式解决

迭代求第n个斐波那契数
int Fib(int n)
{
    int a = 1;
    int b = 1;
    int c = 1;
    while(n>2)
    {
        c = a+b;
        a = b;
        b = c;
        n--;
    }
    return c;
}
提示：

许多问题是以递归的形式进行解释的，这只是因为它比非递归的形式更为清晰。
但是这些问题的迭代实现往往比递归实现效率更高，虽然代码的可读性稍微差些。
当一个问题相当复杂，难以用迭代实现时，此时递归实现的简洁性便可以补偿它所带来的运行时开销

八、函数递归的几个经典题目

1.青蛙跳台阶问题

一只青蛙一次可以跳上 1 级台阶，也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法？

（1）递归求解

和斐波那契数列很相似，跳上第n级的台阶(n>3)，无非就是从n-2跳两级或者n-1的台阶跳1级，那总方法就是f(n)=f(n-2)+f(n-1)
int Fn(int n) {
    if (n <= 2) {
        return n;
    }
    else if (n > 2) {
        return Fn(n - 1) + Fn(n - 2);
    }
}
（2）迭代求解

斐波那契数列是：1 1 2 3 5 8 13······

青蛙跳台阶数列是：1 2 3 5 8 13······
int Fn(int n) {
    int a = 1;
    int b = 2;
    int c = 0;
    if (n == 1) {
        return 1;
    }
    else if (n == 2) {
        return 2;
    }
    else{
        while(n>2){
            c = a + b;
            a = b;
            b = c;
            n--;
        }
    }
    return c;
}
2.汉诺塔问题

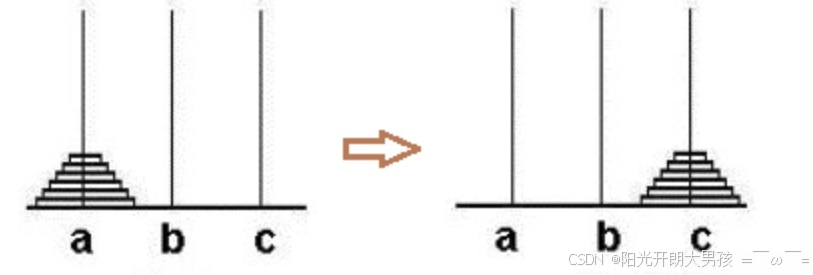
汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？

注意：求得是最少移动次数

（1）简单情形分析

当 n = 1，直接将圆盘从 a 移到 c。
n = 2 时，步骤为 a -> b，a -> c，b -> c。
n = 3 时，步骤为 a -> c，a -> b，c -> b，a -> c，b -> a，b -> c，a -> c。随 n 增大，逐一写步骤不切实际。

（2）核心逻辑剖析

每次移动聚焦将最底下盘子移到目标盘，剩余 n - 1 个盘子形成新汉诺塔问题。以 n = 3 为例，前四步移盘子 3 到 c，之后移剩余盘子到 c 就变成 n = 2 的汉诺塔问题。

（3）简化思考步骤

第一步，将 n - 1 个盘子移到中转柱（又是一个汉诺塔问题）。
第二步，移最底下盘子到目标柱。
第三步，将中转柱上 n - 1 个盘子移到目标柱（是汉诺塔问题）。通过此思路可推导 n 个盘子最少移动步数，类似高中数列问题，可用数学归纳法求解。

以三阶汉诺塔图例：

根据以上思路推出N阶汉诺塔：

手写推导：

（4）移动细节规律

若初始柱盘子数为偶数，第一步将最上面盘子移到中转柱；若为奇数，则移到目标柱。此规律有助于理解移动策略，

（5）代码
#include <stdio.h>

// 定义移动函数，用于输出从柱子x移动到柱子y的操作提示
void move(char x, char y) {
    printf("%c->%c ", x, y);
}

// hanoi函数用于解决汉诺塔问题，通过递归实现盘子的移动
// n表示要移动的盘子数量，pos1为初始柱，pos2为中转柱，pos3为目标柱
void hanoi(int n, char pos1, char pos2, char pos3) {
    if (n == 1) {
        // 当只有一个盘子时，直接从初始柱移动到目标柱
        move(pos1, pos3);
    } else {
        // 先将n - 1个盘子从初始柱pos1借助目标柱pos3移动到中转柱pos2
        hanoi(n - 1, pos1, pos3, pos2);

        // 把最底下的盘子从初始柱pos1移动到目标柱pos3
        move(pos1, pos3);

        // 再将中转柱pos2上的n - 1个盘子借助初始柱pos1移动到目标柱pos3
        hanoi(n - 1, pos2, pos1, pos3);
    }
}

int main() {
    int n = 0;
    scanf("%d", &n);
    hanoi(n, 'a', 'b', 'c');
    return 0;
}

C 语言函数：数字江湖的秘籍要诀与侠义传功

一、函数的概念

二、C语言中函数的分类

1. 库函数

（1）为什么会有库函数？

（2）学习几个库函数

sqrt

strcpy

memset

（3）如何学会使用库函数？

2.自定义函数

（1）函数的组成：

（2）函数举例

找出两个整数中的最大值

交换两个整形变量

三、函数的参数

1. 实际参数（实参）

2.形式参数（形参）

3.实参和形参的关系

四、函数的调用

1.传值调用

2.传址调用

3.实战演练

（1）判断一个数是不是素数

（2）判断一年是不是闰年

（3）每调用一次函数，使变量值增加 1

五、函数的嵌套调用和链式访问

1. 嵌套调用

2. 链式访问

六、函数的声明和定义

1. 函数声明

2. 函数定义（多文件）

七、函数递归

1. 什么是递归？

（1）递归的概念

（2）递归的两个必要条件

2.递归举例

（1）求n的阶乘

（2）顺序打印一个整数的每一位

3.递归与迭代

（1）递归的优缺点

（2）递归与迭代的对比

递归求第n个斐波那契数

迭代求第n个斐波那契数

八、函数递归的几个经典题目

1.青蛙跳台阶问题

（1）递归求解

（2）迭代求解

2.汉诺塔问题

（1）简单情形分析

（2）核心逻辑剖析

（3）简化思考步骤

（4）移动细节规律

（5）代码

悦读