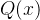目录
命题逻辑
命题:一个具有确切真值的陈述句,或真或假,不能既真又假
真命题:真值为T或1
假命题:真值为F或0
涉及命题的逻辑领域称为命题演算或命题逻辑
令 p、q 为命题
否定运算符:┐p “非p”
逻辑运算符(联结词):
合取 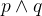
析取 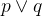
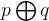
兼或:析取式为真,两命题之一为真或者两者均为真都可以
异或:析取式为真,当p和q中恰好只有一个为真时命题为真
条件语句(蕴含):令 p、q 为命题,条件语句 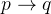
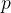
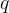
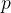
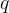
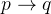
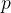
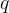
| 如果p,则q | 如果p,q |
| p是q的充分条件 | q的充分条件是p |
| q是p的必要条件 | p的必要条件是q |
| p蕴含q | q如果p |
| q当p | q每当p |
| q除非¬p | q仅当p |
| q由p得出 |
双条件语句(双向蕴含):令 p、q 为命题,条件语句 
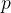
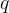
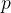
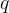
| p是q的充分必要条件 |
| 如果p那么q,反之亦然 |
| p当且仅当q |


| 原命题 |  |
| 逆命题 |  |
| 逆否命题 | ┐ ┐ ┐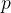 |
| 反命题 | ┐ ┐ ┐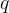 |
等价:两个复合命题总是具有相同真值
一个条件语句与它的逆否命题等价
一个条件语句的逆命题与反命题等价
| 运算符 | 优先级 |
| ┐ | 1 |
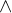 | 2 |
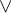 | 3 |
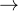 | 4 |
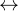 | 5 |
布尔变量:如果一个变量的值或为真或为假,则此变量就称为布尔变量;
用 1 代表真,用 0 代表假
位串:0位或多位的序列。位串的长度就是它所含位的数目。
eg. 01 1011 0110
11 0001 1101
按位OR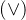
按位AND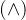
按位XOR
命题等价式
永真式(重言式):一个真值永远是真的复合命题 
矛盾式:一个真值永远为假的复合命题 
可能式:既不是永真式又不是矛盾式的复合命题
逻辑等价:在所有可能的情况下都有相同真值的两个复合命题
如果 

德摩根定律应用:一个析取式的否定是由各分命题否定的合取式组成的
一个合取式的否定是由各分命题否定的析取式组成的
如果 p 和 q 是逻辑等价的,q 和 r 是逻辑等价的,那么 p 和 r 也是逻辑等价的
命题的可满足性:如果存在一个对其变元的真值赋值使其为真,即只需要找到一个特定的使得复合命题为真的真值赋值,这样一个赋值称为这个特定的可满足性问题的一个解
命题的不可满足性:当复合命题对所有变元的真值赋值都是假的,即当且仅当它的否定对所有变元的真值赋值都是真的(当且仅当它的否定是永真式)
谓词
谓词:表明语句的主语具有的性质
一般地,涉及n个变量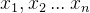
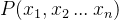
形式为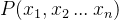
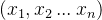
"x>3",分成两个部分,第一部分即变量x是语句的主语,第二部分(谓词”大于3“)表明语句的主语具有的一个性质。用P(x)表示"x大于3".
命题P(x):命题函数P在x的值,一旦给变量x赋一个值,语句P(x)就成为命题并具有真值
谓词常用于验证计算机程序 前置条件:描述合法输入的语句
后置条件:程序运行的输出应该满足的条件
量词
量化:表示在何种程度上谓词对一定范围的个体成立
谓词演算:处理谓词和量词的逻辑领域
全称量词:某一性质对于变量在某一特定域内的所有值均为真
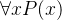
论域(全体域、域):这一特定域
论域规定了变量x所有可能取的值,使用全称量词时必须指定论域
当论域中的所有元素可以一 一列出时,全称量化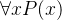
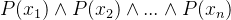
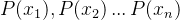
存在量词:有一个个体使得某种性质成立
该命题为真当且仅当论域中至少有一个x的值使得P(x)为真
使用全称量词时必须指定论域
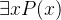
"对某个x,P(x)"
当论域中的所有元素可以一 一列出时,存在量化 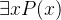
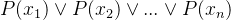
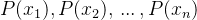
唯一性量词 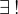
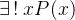
一般避用唯一性量词,用存在量词&全称量词&命题逻辑来表示唯一性。
约束论域的量词:限定一个量词的论域时采用简写的方式,变量必须满足的条件直接放在量词后面。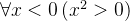
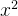
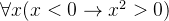
全称量化的约束和一个条件语句的全称量化等价
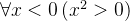
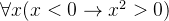
存在量化的约束和一个合取式的存在量化等价
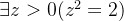
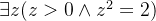
量词 

一个变量是约束的:当量词作用于x。
一个变量是自由的:没有被量词约束或设置为等于某一特定值;或者说变量在公式中所有限定该变量的量词的作用域之外。
这个量词的作用域:逻辑表达式中一个量词作用到的部分。
命题函数中的所有变量出现必须是约束的或者被设置为等于某个特定值的,才能把它转变为一个命题。

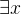

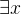
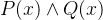
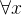
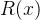
量词的逻辑等价式
涉及谓词和量词的语句是逻辑等价的当且仅当无论用什么谓词代入这些语句,也无论为这些命题函数里的变量 指定什么论域,它们都有相同的真值。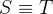
全称量词对于一个合取式是可分配的:
存在量词对于一个析取式是可分配的:
量化表达式的否定 ┐
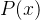
┐

何时为真:对每个x,P(x)为假
何时为假:有x,使P(x)为真
┐
┐ 

何时为真:有x使P(x)为假
何时为假:对每个x,P(x)为真
嵌套量词
嵌套量词:即一个量词出现在另一个量词的作用域内
将量化当作循环:处理多个变量的量化式时,借助嵌套循环来思考
 | 先对x的所有值做循环,而对x的每个值再对y的所有值做循环 |
 | 对x的每个值循环,对y的值循环直到找到一个y使P(x,y)为真 |
 | 对x的值循环直到找到某个x,就这个x对y的所有值循环时P(x,y)总是为真 |
 | 对x的值进行循环,循环时对x的每个值都对y的值循环,直到找到一个xy对P(x,y)成立 |
量词顺序
在没有其他量词的语句中,在不改变量化式意义的前提下嵌套全称量词的顺序可以改变
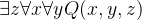
嵌套量词的否定
嵌套量词的否定通过连续地应用单个量词语句的否定规则来得到
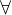
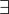
eg.¬