题目

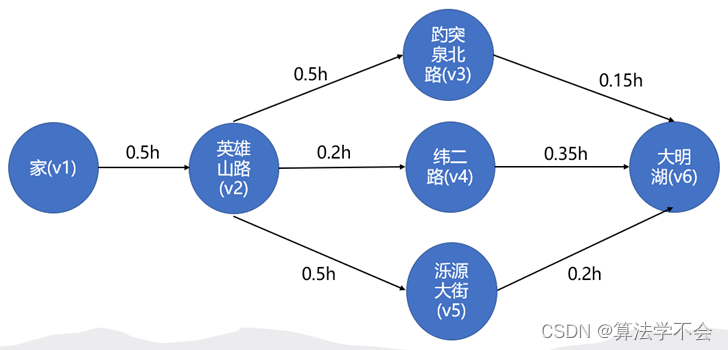
李晓明一家计划在 3月份进行春游，他们将驾车去大明湖游玩。为了节约在路上的时间，李晓明需要提前规划从家到大明湖的路线，使得在路上的时间最短。图 6-55所示为从家到大明湖的可选路线，图中的数值为某段路程驾车时间。

实验要求

（1）将上图看作一个有向图，创建该有向图，并使用数组表示法存储；
（2）使用 Dijkstra 算法求从家到大明湖的最短路径，并将其输出；
（3）根据求出的最短路径计算李晓明制定的路线总共需要多少时间。

主要算法实现

1.图的存储
（1）创建二维数组g用来存储邻接矩阵。
（2）初始化：为方便计算，把图中每条路的权值乘100后赋值到二维数组g中相应的单元,除此之外的单元赋值INF。
2.迪杰斯特拉算法
（1）定义states 辅助数组，用来存储每个节点是否已经找到了最短路径，states[i] = true 表示起点到"顶点i"的最短路径已成功获取，pre 数组用来存储每个节点的前驱节点，dist 数组用来存储每个节点的最短路径距离。
（2）初始化:dist 数组中的每个数据用memset函数初始化为INF，给 dist 数组0下标的单元赋值0（自身的距离为0）。
（2）遍历这个节点所在邻接矩阵的一行的所有距离，如果遍历出的顶点j未被访问过且离这个顶点最近，在states数组中标记顶点j为已经获取到最短路径，之后更新"未获取最短路径的顶点的最短路径和前驱顶点"。（因为此时由于一个新的有最短路径节点的产生会使其他与其相连接的节点的最短路径产生变化）。
（3）在新加入的确定最短路径的顶点j所在邻接的一行遍历，如果这个点和j的距离等于INF，说明其与j不相连，所以不用管，路径长度不变；否则相连，顶点j与原点的最小路径+k与这个点的最小路径，也就是当前这个点的最小路径，如果这个点还没有确定最小路径且当前这个点的最小路径小于之前的路径，更新最小路径和前驱。
（4）当所有的点都获取到最短路径后，循环停止，从终点开始寻找前驱节点，找到后，前驱节点的值赋给终点，继续寻找此前驱节点的前驱节点，直到终点等于起点结束循环，输出时建立一个数组用来存储每个节点的前驱节点对应的序号，此时的顺序是逆序，将数组中的各个节点对应数组中的索引转换为汉字倒着输出即为最短路线

代码实现

#include <iostream>
#include <cstring>
using namespace std;
const int N = 6;
int g[N][N], dist[N], pre[N];
bool states[N];
const string s[N] = {"家", "英雄山路", "趵突泉北路", "泺源大街", "纬二路", "大明湖"};
int main() {
    //初始化
    memset(g, 0x3f,sizeof g);
    g[0][1] = 50;
    g[1][2] = 50;
    g[1][4] = 20;
    g[1][3] = 50;
    g[2][5] = 15;
    g[3][5] = 20;
    g[4][5] = 35;
    memset(dist, 0x3f,sizeof dist);
    dist[0] = 0;
    for (int i = 0; i < N; i++) {
        int t = -1;
        for (int j = 0; j < N; j++) {
            if (!states[j] && (t == -1 || dist[j] < dist[t])) {
                t = j;
            }
        }
        states[t] = true;
        for (int j = 0; j < N; j++) {
            if (dist[j] > g[t][j] + dist[t]) {
                dist[j] = g[t][j] + dist[t];
                pre[j] = t;
            }
        }
    }
    int path[N];
    int cnt = 0;
    for (int i=N-1; i!=0; i=pre[i]) {
        path[cnt++] = i;
    }
    path[cnt++] = 0;
    cout << "从家到大明湖的最短路径是: " << s[path[cnt-1]];
    for (int i = cnt-2; i>=0; i--) {
        cout << "->" << s[path[i]];
    }
    cout << endl;
    cout <<  "从家到大明湖的最短时间是: " << (double)dist[5]/100 << "h" << endl;
    return 0;
}