一、题目

. - 力扣（LeetCode）. - 备战技术面试？力扣提供海量技术面试资源，帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。https://leetcode.cn/problems/TVdhkn/submissions/544682490/

二、题解

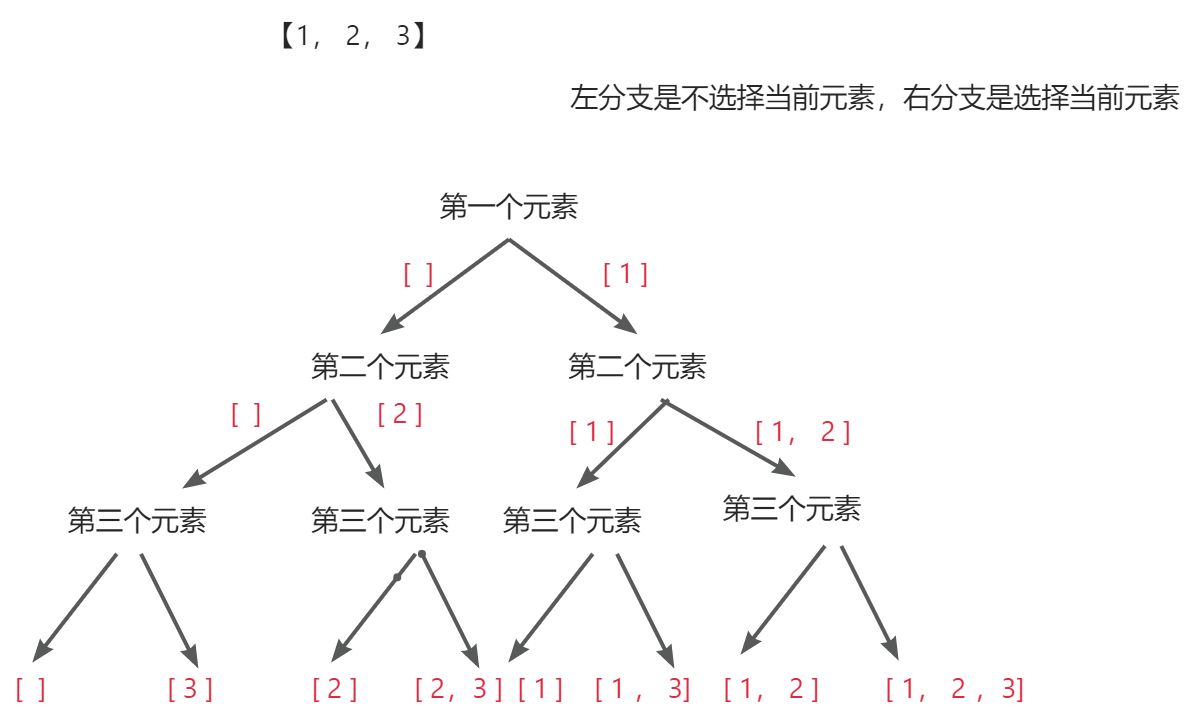
枚举当前元素选或者不选

对应这样一个序列1 2 3， 对于这个序列的第一个元素，在最终的答案中对于每一个位置的元素，都可以选择选他或者不选他

class Solution {
public:
    vector<vector<int>> res;
    vector<int> nums;
    vector<int> path;
    int n;

    void dfs(int u) {
        if (u == n) {
            res.push_back(vector<int>(path));
            return;
        }
        // 选择当前元素
        path.push_back(nums[u]);
        // 选择当前元素的分支
        dfs(u + 1);
        // 回复现场
        path.pop_back();
        // 不选当前元素的分支
        dfs(u + 1);
    }

    vector<vector<int>> subsets(vector<int>& _nums) {
        nums = _nums;
        n = nums.size();
        dfs(0);
        return res;
    }
};

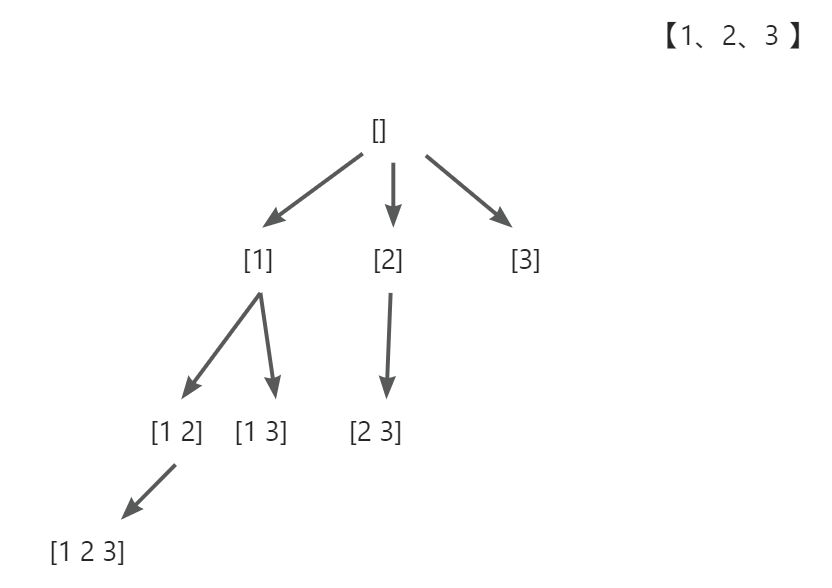
枚举每个位置的情况

枚举每一个位置可能的情况，比如1 2 3这个序列，我们每次都去枚举当前位置可能的元素，比如刚开始是空，将空加入结果集合，然后第一个位置可以枚举1，当第一个位置枚举1之后，第二个位置如何选择呢，第二个位置一定是从1这个元素之后去选择，可以选择2、3变为1 2 或者 13，继续当第二位置选择2时，我们需要从2后面继续选择第三个位置作为1 2 这个序列的第三个元素，2之后只能选择3，如果第二个位置选时，我们需要从3后面选择13序列的第三个元素，3后面没有就不能选择

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path, nums;
    int n;

    void dfs(int u) {
        // 每一个节点都加入
        res.push_back(path);

        // 遍历当前每一个可以选择的元素
        for (int i = u; i < n; i++) {
            path.push_back(nums[i]);
            dfs(i + 1);
            path.pop_back();
        }
    }

    vector<vector<int>> subsets(vector<int>& _nums) {
        nums = _nums;
        n = nums.size();
        dfs(0);
        return res;
    }
};

class Solution {
    List<List<Integer>> res;
    int[] nums;
    List<Integer> path;
    boolean check[];
    int n;

    public void dfs(int u) {
        res.add(new ArrayList<>(path));
        for (int i = u; i < n; i++) {
            path.add(nums[i]);
            dfs(i + 1);
            path.remove(path.size() - 1);
        }
    }

    public List<List<Integer>> subsets(int[] _nums) {
        res = new ArrayList<>();
        nums = _nums;
        n = nums.length;
        check = new boolean[n];
        path = new ArrayList<>();
        dfs(0);
        return res;
    }
}