Bootstrap

第二次CCF计算机软件能力认证

AcWing 3202. 相邻数对

给定 n 个不同的整数，问这些数中有多少对整数，它们的值正好相差 1。

输出格式

输入的第一行包含一个整数 n，表示给定整数的个数。

第二行包含所给定的 n 个整数。

输出格式

输出一个整数，表示值正好相差 1 的数对的个数。

数据范围

1≤n≤1000
给定的整数为不超过 10000 的非负整数。

输入样例

6
10 2 6 3 7 8

输出样例

3

样例解释

值正好相差 1 的数对包括 (2,3),(6,7),(7,8)

排序 AC: 

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e3+5;
int n,a[N],ans;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+1+n);
    for(int i=1;i<n;i++) if(a[i]+1==a[i+1]) ans++;
    cout<<ans<<endl;
    return 0;
}

AcWing 3203. 画图

在一个定义了直角坐标系的纸上，画一个 (x1,y1) 到 (x2,y2) 的矩形指将横坐标范围从 x1 到 x2，纵坐标范围从 y1 到 y2 之间的区域涂上颜色。

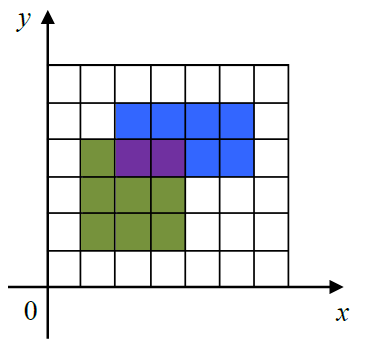
下图给出了一个画了两个矩形的例子。

第一个矩形是 (1,1) 到 (4,4)，用绿色和紫色表示。

第二个矩形是 (2,3) 到 (6,5)，用蓝色和紫色表示。

图中，一共有 15 个单位的面积被涂上颜色，其中紫色部分被涂了两次，但在计算面积时只计算一次。

在实际的涂色过程中，所有的矩形都涂成统一的颜色，图中显示不同颜色仅为说明方便。

p21.png

给出所有要画的矩形，请问总共有多少个单位的面积被涂上颜色。

输入格式

输入的第一行包含一个整数 n，表示要画的矩形的个数。

接下来 n 行，每行 4 个非负整数，分别表示要画的矩形的左下角的横坐标与纵坐标，以及右上角的横坐标与纵坐标。

输出格式

输出一个整数，表示有多少个单位的面积被涂上颜色。

数据范围

1≤n≤100
0≤ 横坐标、纵坐标 ≤100

输入样例

2
1 1 4 4
2 3 6 5

输出样例

15

标记数组计数 AC:

#include<iostream>
using namespace std;
const int N=1e2+5;
int n,ans;
bool flag[N][N];
int main(){
    cin>>n;
    while(n--){
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        for(int i=x1;i<x2;i++) for(int j=y1;j<y2;j++) flag[i][j]=true;
    }
    for(int i=0;i<N;i++) for(int j=0;j<N;j++)  if(flag[i][j]) ans++;
    cout<<ans<<endl;
    return 0;
}

AcWing 3204. 字符串匹配

给出一个字符串和多行文字，在这些文字中找到字符串出现的那些行。

你的程序还需支持大小写敏感选项：当选项打开时，表示同一个字母的大写和小写看作不同的字符；当选项关闭时，表示同一个字母的大写和小写看作相同的字符。

输入格式

输入的第一行包含一个字符串 S，由大小写英文字母组成。

第二行包含一个数字，表示大小写敏感的选项，当数字为 0 时表示大小写不敏感，当数字为 1 时表示大小写敏感。

第三行包含一个整数 n，表示给出的文字的行数。

接下来 n 行，每行包含一个字符串，字符串由大小写英文字母组成，不含空格和其他字符。

输出格式

输出多行，每行包含一个字符串，按出现的顺序依次给出那些包含了字符串 S 的行。

数据范围

1≤n≤100
每个字符串的长度不超过 100

输入样例

Hello
1
5
HelloWorld
HiHiHelloHiHi
GrepIsAGreatTool
HELLO
HELLOisNOTHello

输出样例

HelloWorld
HiHiHelloHiHi
HELLOisNOTHello

样例解释

在上面的样例中，第四个字符串虽然也是 Hello，但是大小写不正确。

如果将输入的第二行改为 0，则第四个字符串应该输出。

模拟 AC: 

#include<iostream>
#include<cstring>//a-z 97-122  A-Z 65-90
using namespace std;
string s;
int flag,n;
bool check_0(string a,string b,int x){
    for(int i=0;i<x;i++) if(abs((int)a[i]-(int)b[i])!=0&&abs((int)a[i]-(int)b[i])!=32) return false;
    return true;
}
bool check_1(string a,string b,int x){
    for(int i=0;i<x;i++) if(a[i]!=b[i]) return false;
    return true;
}
int main(){
    cin>>s>>flag>>n;
    int len=s.size();
    while(n--){
        string t;
        cin>>t;
        int len_t=t.size();
        for(int i=0;i<=len_t-len;i++){
            string temp=t.substr(i,i+len);
            if(flag==0&&check_0(temp,s,len)) {cout<<t<<endl;break;}
            if(flag==1&&check_1(temp,s,len)) {cout<<t<<endl;break;}
        }
    }
    return 0;
}

AcWing 3205. 最优配餐

栋栋最近开了一家餐饮连锁店，提供外卖服务。

随着连锁店越来越多，怎么合理的给客户送餐成为了一个急需解决的问题。

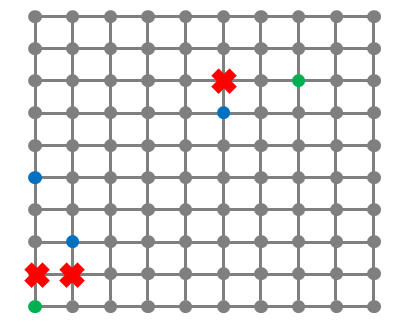
栋栋的连锁店所在的区域可以看成是一个 n×n 的方格图（如下图所示），方格的格点上的位置上可能包含栋栋的分店（绿色标注）或者客户（蓝色标注），有一些格点是不能经过的（红色标注）。

方格图中的线表示可以行走的道路，相邻两个格点的距离为 1。

栋栋要送餐必须走可以行走的道路，而且不能经过红色标注的点。

p41.png

送餐的主要成本体现在路上所花的时间，每一份餐每走一个单位的距离需要花费 1 块钱。

每个客户的需求都可以由栋栋的任意分店配送，每个分店没有配送总量的限制。

现在你得到了栋栋的客户的需求，请问在最优的送餐方式下，送这些餐需要花费多大的成本。

输入格式

输入的第一行包含四个整数 n,m,k,d，分别表示方格图的大小、栋栋的分店数量、客户的数量，以及不能经过的点的数量。

接下来 m 行，每行两个整数 xi,yi，表示栋栋的一个分店在方格图中的横坐标和纵坐标。

接下来 k 行，每行三个整数 xi,yi,ci，分别表示每个客户在方格图中的横坐标、纵坐标和订餐的量。（注意，可能有多个客户在方格图中的同一个位置）

接下来 d 行，每行两个整数，分别表示每个不能经过的点的横坐标和纵坐标。

输出格式

输出一个整数，表示最优送餐方式下所需要花费的成本。

数据范围

前 30% 的评测用例满足：1≤n≤20
前 60% 的评测用例满足：1≤n≤100
所有评测用例都满足：1≤n≤1000,1≤m,k,d≤n^2,1≤xi,yi≤n
可能有多个客户在同一个格点上。
每个客户的订餐量不超过 1000 每个客户所需要的餐都能被送到。

输入样例

10 2 3 3
1 1
8 8
1 5 1
2 3 3
6 7 2
1 2
2 2
6 8

输出样例

29

在做这题前,可以先回顾一下模板题: 

多源bfs问题:

AcWing 173. 矩阵距离(模板题)

给定一个 N 行 M 列的 01 矩阵 A，A[i][j]与 A[k][l] 之间的曼哈顿距离定义为：

dist(A[i][j],A[k][l])=|i−k|+|j−l|

输出一个 N 行 M 列的整数矩阵 B，其中：

B[i][j]=min1≤x≤N,1≤y≤M,A[x][y]=1dist(A[i][j],A[x][y])

输入格式

第一行两个整数 N,M

接下来一个 N 行 M 列的 01 矩阵，数字之间没有空格。

输出格式

一个 N 行 M 列的矩阵 B，相邻两个整数之间用一个空格隔开。

数据范围

1≤N,M≤1000

输入样例

3 4
0001
0011
0110

输出样例

3 2 1 0
2 1 0 0
1 0 0 1

 矩阵距离 AC:

#include<iostream>
#include<queue>
using namespace std;
const int N=1e3+5;
int n,m,dist[N][N],dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
bool flag[N][N];
char G[N][N];
void bfs(){
    queue<pair<int,int>>q;
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(G[i][j]=='1') {flag[i][j]=true; q.push({i,j});}
    while(!q.empty()){
        auto t=q.front();
        int x=t.first,y=t.second;
        q.pop();
        for(int i=0;i<4;i++){
            int xx=x+dx[i],yy=y+dy[i];
            if(xx>=1&&xx<=n&&yy>=1&&yy<=m){
                if(!flag[xx][yy]){
                    flag[xx][yy]=true;
                    dist[xx][yy]=dist[x][y]+1;
                    q.push({xx,yy});
                }
            }
        }
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>G[i][j];
    bfs();
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cout<<dist[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}

最优配餐 AC:

注意: 开 long long 以及 提高输入输出的效率 

#include<iostream>
#include<queue>
#define int long long
using namespace std;
const int N=1e3+5;
int n,m,k,d,res,dist[N][N],ans[N][N],dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
bool flag[N][N];
char G[N][N];
void bfs(){
    queue<pair<int,int>>q;
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(G[i][j]=='0') {flag[i][j]=true; q.push({i,j});}
    while(!q.empty()){
        auto t=q.front();
        int x=t.first,y=t.second;
        q.pop();
        for(int i=0;i<4;i++){
            int xx=x+dx[i],yy=y+dy[i];
            if(xx>=1&&xx<=n&&yy>=1&&yy<=n){
                if(!flag[xx][yy]&&G[xx][yy]=='1'){
                    flag[xx][yy]=true;
                    dist[xx][yy]=dist[x][y]+1;
                    q.push({xx,yy});
                }
            }
        }
    }
}
signed main(){
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>m>>k>>d;
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) G[i][j]='1';
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        G[x][y]='0';
    }
    for(int i=1;i<=k;i++){
        int x,y,c;
        cin>>x>>y>>c;
        ans[x][y]+=c;
    }
    for(int i=1;i<=d;i++){
        int x,y;
        cin>>x>>y;
        G[x][y]='#';
    }
    bfs();
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) res+=dist[i][j]*ans[i][j];
    cout<<res<<endl;
    return 0;
}

AcWing 3206. 拼图

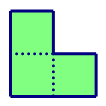
给出一个 n×m 的方格图，现在要用如下 L 型的积木拼到这个图中，使得方格图正好被拼满，请问总共有多少种拼法。

其中，方格图的每一个方格正好能放积木中的一块。

积木可以任意旋转。

p51.png

输入格式

输入的第一行包含两个整数 n,m，表示方格图的大小。

输出格式

输出一行，表示可以放的方案数，由于方案数可能很多，所以请输出方案数除以 10^9+7 的余数。

数据范围

在评测时将使用 10 个评测用例对你的程序进行评测。
评测用例 1 和 2 满足：1≤n≤30，m=2
评测用例 3 和 4 满足：1≤n,m≤6
评测用例 5 满足：1≤n≤100，1≤m≤6
评测用例 6 和 7 满足：1≤n≤1000，1≤m≤6
评测用例 8、9 和 10 满足：1≤n≤10^15，1≤m≤7

输入样例

6 2

输出样例

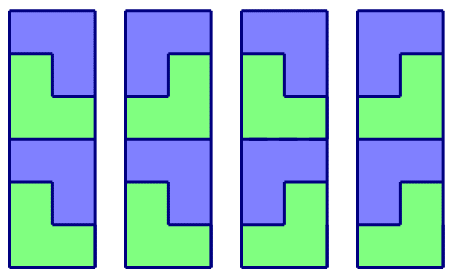
4

样例解释

四种拼法如下图所示：

p52.png

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
MyBatis学习指南
DenseNet分类网络改进（添加SPP）--亲测有效
表面粗糙度：Ra，Ry 、Rz 的区别 | 金属磨损 | 表面处理
STM32 驱动 ESP8266 WIFI 模块
python实验三，根据文本画出词云（外加词性分析、高频词统计）
java中switch编译结果探秘
【数据结构与算法】第4课—数据结构单链表OJ练习题
Gradle 安装配置详解
文字与格式字符串不匹配
探索未来滚动体验：Vue3-Marquee
;