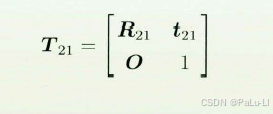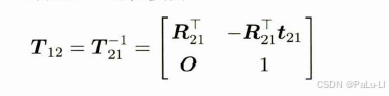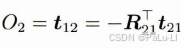前言
ORB-SLAM2源码学习:Initializer.cc⑦: Initializer::Triangulate特征点对的三角化_cv::svd::compute-CSDN博客
经过上面的三角化我们成功得到了三维点,但是经过三角化成功的三维点并不一定是有效的,需要筛选才能作为初始化地图点。
1.函数声明
int Initializer::CheckRT(const cv::Mat &R, const cv::Mat &t, const vector<cv::KeyPoint> &vKeys1, const vector<cv::KeyPoint> &vKeys2,
const vector<Match> &vMatches12, vector<bool> &vbMatchesInliers,
const cv::Mat &K, vector<cv::Point3f> &vP3D, float th2, vector<bool> &vbGood, float ¶llax)2.函数定义
我们把相机1的光轴中心作为世界坐标系的原点,从相机1到相机2的位姿:
则从相机2到相机1的位姿:
对应关系:
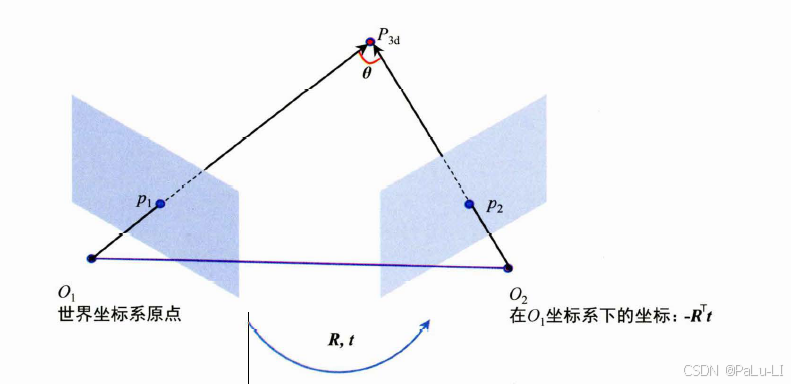
则相机2的光轴中心O2在相机1的坐标系下的坐标为:
计算相机2 的光轴中心O2 在相机1 坐标系下的坐标是为了求解三维点分别在两个坐标系下和光轴中心的夹角。如果我们要求向量夹角,那么前提是这些向量都在同一个坐标系下。我们看相机1坐标系,此时O1是相机1 的光轴中心,也是相机1 坐标系原点, P3d 是相机1坐标系(世界坐标系)下的三维点,这就必须得到O2在相机1 坐标系下的坐标,也就是我们前面推导的过程。
计算夹角是为了判断三维点的有效性, 因为初始化地图点( 三角化得到的三维点)特别重要,后续跟踪都是以此为基础的,所以在确定三维点时要非常小心。确定一个合格的三维点需要通过以下条件:
1.三维点的3 个坐标都必须是有限的实数。
2.三维点深度值必须为正。
3.三维点和两帧图像光轴中心夹角需要满足一定的条件。夹角越大,视差越大, 三角化结果越准确。
4. 三维点的重投影误差小于设定的阈值。
经过上面条件的筛选,最后剩下的三维点才是合格的三维点。我们会记录当前位姿对应的合格三维点数目和视差。
具体的流程
1.计算前的参数准备与声明
// 对给出的特征点对及其R t , 通过三角化检查解的有效性,也称为 cheirality check
// Calibration parameters
//从相机内参数矩阵获取相机的校正参数
const float fx = K.at<float>(0,0);
const float fy = K.at<float>(1,1);
const float cx = K.at<float>(0,2);
const float cy = K.at<float>(1,2);
//特征点是否是good点的标记,这里的特征点指的是参考帧中的特征点
vbGood = vector<bool>(vKeys1.size(),false);
//重设存储空间坐标的点的大小
vP3D.resize(vKeys1.size());
//存储计算出来的每对特征点的视差
vector<float> vCosParallax;
vCosParallax.reserve(vKeys1.size());
2.构建投影矩阵计算相机光心2在世界坐标系下的坐标
这里与前边推导的过程一致。
// Camera 1 Projection Matrix K[I|0]
// Step 1:计算相机的投影矩阵
// 投影矩阵P是一个 3x4 的矩阵,可以将空间中的一个点投影到平面上,获得其平面坐标,这里均指的是齐次坐标。
// 对于第一个相机是 P1=K*[I|0]
// 以第一个相机的光心作为世界坐标系, 定义相机的投影矩阵
cv::Mat P1(3,4, //矩阵的大小是3x4
CV_32F, //数据类型是浮点数
cv::Scalar(0)); //初始的数值是0
//将整个K矩阵拷贝到P1矩阵的左侧3x3矩阵,因为 K*I = K
K.copyTo(P1.rowRange(0,3).colRange(0,3));
// 第一个相机的光心设置为世界坐标系下的原点
cv::Mat O1 = cv::Mat::zeros(3,1,CV_32F);
// Camera 2 Projection Matrix K[R|t]
// 计算第二个相机的投影矩阵 P2=K*[R|t]
cv::Mat P2(3,4,CV_32F);
R.copyTo(P2.rowRange(0,3).colRange(0,3));
t.copyTo(P2.rowRange(0,3).col(3));
//最终结果是K*[R|t]
P2 = K*P2;
// 第二个相机的光心在世界坐标系下的坐标
cv::Mat O2 = -R.t()*t;3.开始遍历所有的特征点对
//在遍历开始前,先将good点计数设置为0
int nGood=0;
// 开始遍历所有的特征点对
for(size_t i=0, iend=vMatches12.size();i<iend;i++)
{
// 跳过outliers
if(!vbMatchesInliers[i])
continue;
....
} 3.1调用Triangulate函数进行三角化
// Step 2 获取特征点对,调用Triangulate() 函数进行三角化,得到三角化测量之后的3D点坐标
// kp1和kp2是匹配好的有效特征点
const cv::KeyPoint &kp1 = vKeys1[vMatches12[i].first];
const cv::KeyPoint &kp2 = vKeys2[vMatches12[i].second];
//存储三维点的的坐标
cv::Mat p3dC1;
// 利用三角法恢复三维点p3dC1
Triangulate(kp1,kp2, //特征点
P1,P2, //投影矩阵
p3dC1); //输出,三角化测量之后特征点的空间坐标 3.2合格的三维点的条件1的判断
// Step 3 第一关:检查三角化的三维点坐标是否合法(非无穷值)
// 只要三角测量的结果中有一个是无穷大的就说明三角化失败,跳过对当前点的处理,进行下一对特征点的遍历
if(!isfinite(p3dC1.at<float>(0)) || !isfinite(p3dC1.at<float>(1)) || !isfinite(p3dC1.at<float>(2)))
{
//其实这里就算是不这样写也没问题,因为默认的匹配点对就不是good点
vbGood[vMatches12[i].first]=false;
//继续对下一对匹配点的处理
continue;
}3.3合格的三维点的条件2和3的判断
// Check parallax
// Step 4 第二关:通过三维点深度值正负、两相机光心视差角大小来检查是否合法
//得到向量PO1
cv::Mat normal1 = p3dC1 - O1;
//求取模长,其实就是距离
float dist1 = cv::norm(normal1);
//同理构造向量PO2
cv::Mat normal2 = p3dC1 - O2;
//求模长
float dist2 = cv::norm(normal2);
//根据公式:a.*b=|a||b|cos_theta 可以推导出来下面的式子
float cosParallax = normal1.dot(normal2)/(dist1*dist2);
// Check depth in front of first camera (only if enough parallax, as "infinite" points can easily go to negative depth)
// 如果深度值为负值,为非法三维点跳过该匹配点对
// ?视差比较小时,重投影误差比较大。这里0.99998 对应的角度为0.36°,这里不应该是 cosParallax>0.99998 吗?
// ?因为后面判断vbGood 点时的条件也是 cosParallax<0.99998
// !可能导致初始化不稳定
if(p3dC1.at<float>(2)<=0 && cosParallax<0.99998)
continue;
// Check depth in front of second camera (only if enough parallax, as "infinite" points can easily go to negative depth)
// 讲空间点p3dC1变换到第2个相机坐标系下变为p3dC2
cv::Mat p3dC2 = R*p3dC1+t;
//判断过程和上面的相同
if(p3dC2.at<float>(2)<=0 && cosParallax<0.99998)
continue;3.4计算重投影误差
// Step 5 第三关:计算空间点在参考帧和当前帧上的重投影误差,如果大于阈值则舍弃
// Check reprojection error in first image
// 计算3D点在第一个图像上的投影误差
//投影到参考帧图像上的点的坐标x,y
float im1x, im1y;
//这个使能空间点的z坐标的倒数
float invZ1 = 1.0/p3dC1.at<float>(2);
//投影到参考帧图像上。因为参考帧下的相机坐标系和世界坐标系重合,因此这里就直接进行投影就可以了
im1x = fx*p3dC1.at<float>(0)*invZ1+cx;
im1y = fy*p3dC1.at<float>(1)*invZ1+cy;
//参考帧上的重投影误差,这个的确就是按照定义来的
float squareError1 = (im1x-kp1.pt.x)*(im1x-kp1.pt.x)+(im1y-kp1.pt.y)*(im1y-kp1.pt.y);
// 重投影误差太大,跳过淘汰
if(squareError1>th2)
continue;
// Check reprojection error in second image
// 计算3D点在第二个图像上的投影误差,计算过程和第一个图像类似
float im2x, im2y;
// 注意这里的p3dC2已经是第二个相机坐标系下的三维点了
float invZ2 = 1.0/p3dC2.at<float>(2);
im2x = fx*p3dC2.at<float>(0)*invZ2+cx;
im2y = fy*p3dC2.at<float>(1)*invZ2+cy;
// 计算重投影误差
float squareError2 = (im2x-kp2.pt.x)*(im2x-kp2.pt.x)+(im2y-kp2.pt.y)*(im2y-kp2.pt.y);
// 重投影误差太大,跳过淘汰
if(squareError2>th2)
continue;3.5统计经过检验的三维点信息
// Step 6 统计经过检验的3D点个数,记录3D点视差角
// 如果运行到这里就说明当前遍历的这个特征点对靠谱,经过了重重检验,说明是一个合格的点,称之为good点
vCosParallax.push_back(cosParallax);
//存储这个三角化测量后的3D点在世界坐标系下的坐标
vP3D[vMatches12[i].first] = cv::Point3f(p3dC1.at<float>(0),p3dC1.at<float>(1),p3dC1.at<float>(2));
//good点计数++
nGood++;
//判断视差角,只有视差角稍稍大一丢丢的才会给打good点标记
//? bug 我觉得这个写的位置不太对。你的good点计数都++了然后才判断,不是会让good点标志和good点计数不一样吗
if(cosParallax<0.99998)
vbGood[vMatches12[i].first]=true;4.得到最小的视差角
如果满足要求的三维点数大于50就获取其中最小的视差角如果不满足数量要求就将视差角设置为0。
// Step 7 得到3D点中较小的视差角,并且转换成为角度制表示
if(nGood>0)
{
// 从小到大排序,注意vCosParallax值越大,视差越小
sort(vCosParallax.begin(),vCosParallax.end());
// !排序后并没有取最小的视差角,而是取一个较小的视差角
// 作者的做法:如果经过检验过后的有效3D点小于50个,那么就取最后那个最小的视差角(cos值最大)
// 如果大于50个,就取排名第50个的较小的视差角即可,为了避免3D点太多时出现太小的视差角
size_t idx = min(50,int(vCosParallax.size()-1));
//将这个选中的角弧度制转换为角度制
parallax = acos(vCosParallax[idx])*180/CV_PI;
}
else
//如果没有good点那么这个就直接设置为0了
parallax=0;
//返回good点计数
return nGood;完整的代码分析
/*
用位姿来对特征匹配点三角化,从中筛选中合格的三维点
R 旋转矩阵R
t 平移矩阵t
vKeys1 参考帧特征点
vKeys2 当前帧特征点
vMatches12 两帧特征点的匹配关系
vbMatchesInliers 特征点对内点标记
K 相机内参矩阵
vP3D 三角化测量之后的特征点的空间坐标
th2 重投影误差的阈值
vbGood 标记成功三角化点?
parallax 计算出来的比较大的视差角(注意不是最大,具体看后面代码)
return int
*/
int Initializer::CheckRT(const cv::Mat &R, const cv::Mat &t, const vector<cv::KeyPoint> &vKeys1, const vector<cv::KeyPoint> &vKeys2,
const vector<Match> &vMatches12, vector<bool> &vbMatchesInliers,
const cv::Mat &K, vector<cv::Point3f> &vP3D, float th2, vector<bool> &vbGood, float ¶llax)
{
// 对给出的特征点对及其R t , 通过三角化检查解的有效性,也称为 cheirality check
// Calibration parameters
//从相机内参数矩阵获取相机的校正参数
const float fx = K.at<float>(0,0);
const float fy = K.at<float>(1,1);
const float cx = K.at<float>(0,2);
const float cy = K.at<float>(1,2);
//特征点是否是good点的标记,这里的特征点指的是参考帧中的特征点
vbGood = vector<bool>(vKeys1.size(),false);
//重设存储空间坐标的点的大小
vP3D.resize(vKeys1.size());
//存储计算出来的每对特征点的视差
vector<float> vCosParallax;
vCosParallax.reserve(vKeys1.size());
// Camera 1 Projection Matrix K[I|0]
// Step 1:计算相机的投影矩阵
// 投影矩阵P是一个 3x4 的矩阵,可以将空间中的一个点投影到平面上,获得其平面坐标,这里均指的是齐次坐标。
// 对于第一个相机是 P1=K*[I|0]
// 以第一个相机的光心作为世界坐标系, 定义相机的投影矩阵
cv::Mat P1(3,4, //矩阵的大小是3x4
CV_32F, //数据类型是浮点数
cv::Scalar(0)); //初始的数值是0
//将整个K矩阵拷贝到P1矩阵的左侧3x3矩阵,因为 K*I = K
K.copyTo(P1.rowRange(0,3).colRange(0,3));
// 第一个相机的光心设置为世界坐标系下的原点
cv::Mat O1 = cv::Mat::zeros(3,1,CV_32F);
// Camera 2 Projection Matrix K[R|t]
// 计算第二个相机的投影矩阵 P2=K*[R|t]
cv::Mat P2(3,4,CV_32F);
R.copyTo(P2.rowRange(0,3).colRange(0,3));
t.copyTo(P2.rowRange(0,3).col(3));
//最终结果是K*[R|t]
P2 = K*P2;
// 第二个相机的光心在世界坐标系下的坐标
cv::Mat O2 = -R.t()*t;
//在遍历开始前,先将good点计数设置为0
int nGood=0;
// 开始遍历所有的特征点对
for(size_t i=0, iend=vMatches12.size();i<iend;i++)
{
// 跳过outliers
if(!vbMatchesInliers[i])
continue;
// Step 2 获取特征点对,调用Triangulate() 函数进行三角化,得到三角化测量之后的3D点坐标
// kp1和kp2是匹配好的有效特征点
const cv::KeyPoint &kp1 = vKeys1[vMatches12[i].first];
const cv::KeyPoint &kp2 = vKeys2[vMatches12[i].second];
//存储三维点的的坐标
cv::Mat p3dC1;
// 利用三角法恢复三维点p3dC1
Triangulate(kp1,kp2, //特征点
P1,P2, //投影矩阵
p3dC1); //输出,三角化测量之后特征点的空间坐标
// Step 3 第一关:检查三角化的三维点坐标是否合法(非无穷值)
// 只要三角测量的结果中有一个是无穷大的就说明三角化失败,跳过对当前点的处理,进行下一对特征点的遍历
if(!isfinite(p3dC1.at<float>(0)) || !isfinite(p3dC1.at<float>(1)) || !isfinite(p3dC1.at<float>(2)))
{
//其实这里就算是不这样写也没问题,因为默认的匹配点对就不是good点
vbGood[vMatches12[i].first]=false;
//继续对下一对匹配点的处理
continue;
}
// Check parallax
// Step 4 第二关:通过三维点深度值正负、两相机光心视差角大小来检查是否合法
//得到向量PO1
cv::Mat normal1 = p3dC1 - O1;
//求取模长,其实就是距离
float dist1 = cv::norm(normal1);
//同理构造向量PO2
cv::Mat normal2 = p3dC1 - O2;
//求模长
float dist2 = cv::norm(normal2);
//根据公式:a.*b=|a||b|cos_theta 可以推导出来下面的式子
float cosParallax = normal1.dot(normal2)/(dist1*dist2);
// Check depth in front of first camera (only if enough parallax, as "infinite" points can easily go to negative depth)
// 如果深度值为负值,为非法三维点跳过该匹配点对
// ?视差比较小时,重投影误差比较大。这里0.99998 对应的角度为0.36°,这里不应该是 cosParallax>0.99998 吗?
// ?因为后面判断vbGood 点时的条件也是 cosParallax<0.99998
// !可能导致初始化不稳定
if(p3dC1.at<float>(2)<=0 && cosParallax<0.99998)
continue;
// Check depth in front of second camera (only if enough parallax, as "infinite" points can easily go to negative depth)
// 讲空间点p3dC1变换到第2个相机坐标系下变为p3dC2
cv::Mat p3dC2 = R*p3dC1+t;
//判断过程和上面的相同
if(p3dC2.at<float>(2)<=0 && cosParallax<0.99998)
continue;
// Step 5 第三关:计算空间点在参考帧和当前帧上的重投影误差,如果大于阈值则舍弃
// Check reprojection error in first image
// 计算3D点在第一个图像上的投影误差
//投影到参考帧图像上的点的坐标x,y
float im1x, im1y;
//这个使能空间点的z坐标的倒数
float invZ1 = 1.0/p3dC1.at<float>(2);
//投影到参考帧图像上。因为参考帧下的相机坐标系和世界坐标系重合,因此这里就直接进行投影就可以了
im1x = fx*p3dC1.at<float>(0)*invZ1+cx;
im1y = fy*p3dC1.at<float>(1)*invZ1+cy;
//参考帧上的重投影误差,这个的确就是按照定义来的
float squareError1 = (im1x-kp1.pt.x)*(im1x-kp1.pt.x)+(im1y-kp1.pt.y)*(im1y-kp1.pt.y);
// 重投影误差太大,跳过淘汰
if(squareError1>th2)
continue;
// Check reprojection error in second image
// 计算3D点在第二个图像上的投影误差,计算过程和第一个图像类似
float im2x, im2y;
// 注意这里的p3dC2已经是第二个相机坐标系下的三维点了
float invZ2 = 1.0/p3dC2.at<float>(2);
im2x = fx*p3dC2.at<float>(0)*invZ2+cx;
im2y = fy*p3dC2.at<float>(1)*invZ2+cy;
// 计算重投影误差
float squareError2 = (im2x-kp2.pt.x)*(im2x-kp2.pt.x)+(im2y-kp2.pt.y)*(im2y-kp2.pt.y);
// 重投影误差太大,跳过淘汰
if(squareError2>th2)
continue;
// Step 6 统计经过检验的3D点个数,记录3D点视差角
// 如果运行到这里就说明当前遍历的这个特征点对靠谱,经过了重重检验,说明是一个合格的点,称之为good点
vCosParallax.push_back(cosParallax);
//存储这个三角化测量后的3D点在世界坐标系下的坐标
vP3D[vMatches12[i].first] = cv::Point3f(p3dC1.at<float>(0),p3dC1.at<float>(1),p3dC1.at<float>(2));
//good点计数++
nGood++;
//判断视差角,只有视差角稍稍大一丢丢的才会给打good点标记
//? bug 我觉得这个写的位置不太对。你的good点计数都++了然后才判断,不是会让good点标志和good点计数不一样吗
if(cosParallax<0.99998)
vbGood[vMatches12[i].first]=true;
}
// Step 7 得到3D点中较小的视差角,并且转换成为角度制表示
if(nGood>0)
{
// 从小到大排序,注意vCosParallax值越大,视差越小
sort(vCosParallax.begin(),vCosParallax.end());
// !排序后并没有取最小的视差角,而是取一个较小的视差角
// 作者的做法:如果经过检验过后的有效3D点小于50个,那么就取最后那个最小的视差角(cos值最大)
// 如果大于50个,就取排名第50个的较小的视差角即可,为了避免3D点太多时出现太小的视差角
size_t idx = min(50,int(vCosParallax.size()-1));
//将这个选中的角弧度制转换为角度制
parallax = acos(vCosParallax[idx])*180/CV_PI;
}
else
//如果没有good点那么这个就直接设置为0了
parallax=0;
//返回good点计数
return nGood;
}结束语
以上就是我学习到的内容,如果对您有帮助请多多支持我,如果哪里有问题欢迎大家在评论区积极讨论,我看到会及时回复。