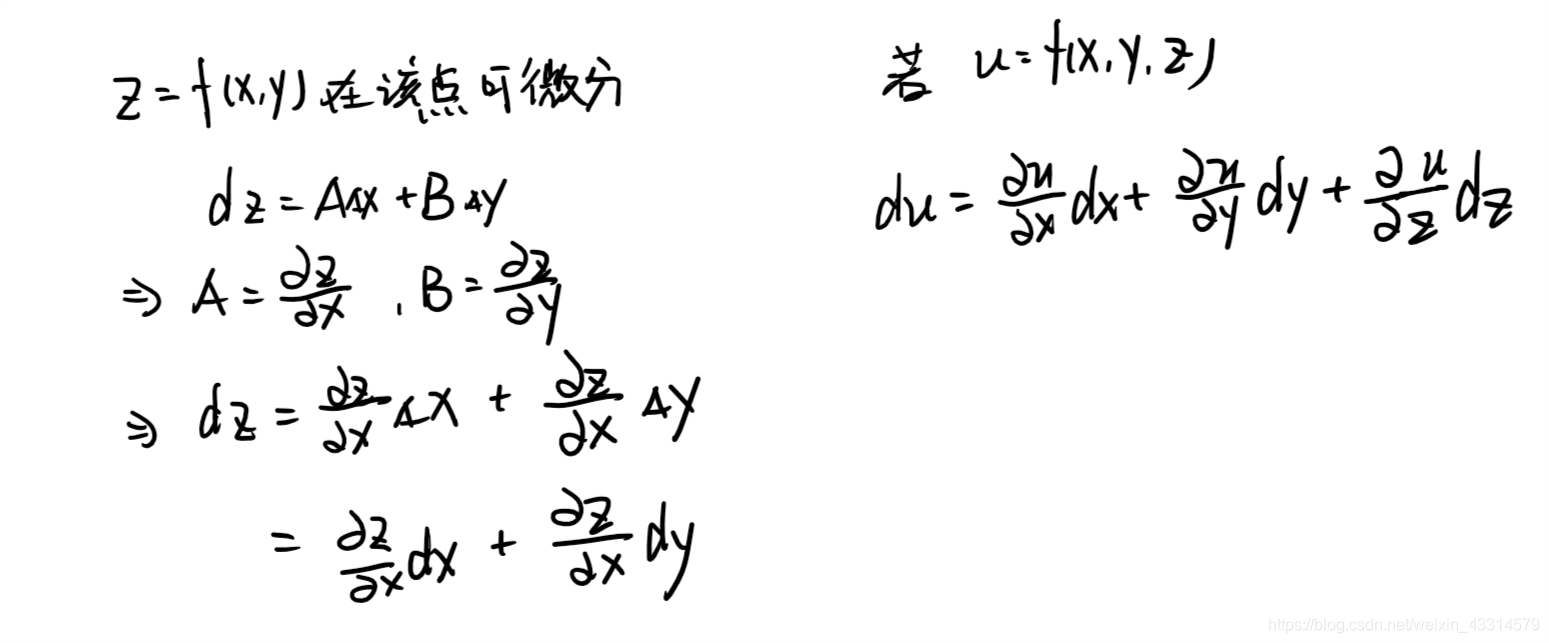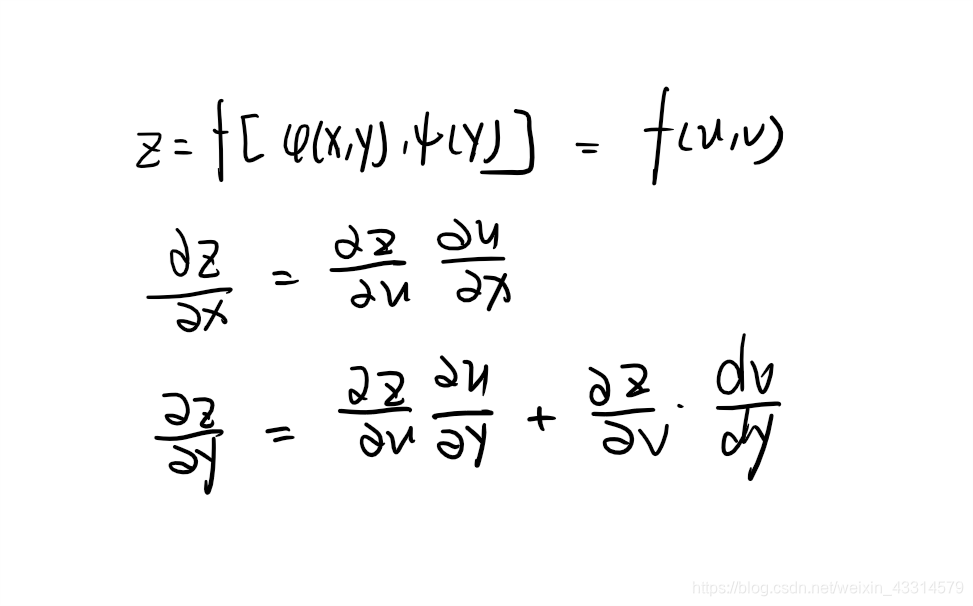偏导数全导数
偏导数
由于是二元函数,有两个因变量。偏导数表示分别对某一个导数求导,如偏x导数、偏y导数。
高阶偏导数
对偏导数继续求导。以二元函数的二阶偏导数为例,偏x导数有两个偏导数、偏y导数有两个偏导数。
定理:如果二元函数的两个二阶混合偏导数连续,那么他们两个相等。
全微分
与一元函数类似,由于有两个变量,x或y的增量称为偏增量,单单对x或y的微分称为偏微分。
若x,y同时增加,称为全增量。
全微分定义见下图
定理
- 如果函数在该点可微分,那么其在该点的偏导数一定存在,且全微分中A、B分别等于偏x导数、偏y导数(叠加定理)
(全微分存在,函数可微分,偏导数一定存在;偏导数存在,全微分不一定存在)
- 如果函数在该点偏导数连续,那么函数在该点可微分
多元复合函数求导
一元函数与多元函数复合
先对多元函数微分,再把每个函数看成一元函数进行求导
多元函数与多元函数复合
如果对x求导,就先对所有函数微分,再把每个函数对x微分,最后相加。对y同理。
其他情形
当多元函数与一元或者多元函数复合时,可能所导变量在某个函数中不存在
不管那种情况,都有一下规律:
把最外层函数里的一个一个函数看过来,如果这个函数不存在所导变量,就不理他看下一个(微分后为0)。如果有,就先把最外层函数对其微分,如果里面这个函数是一元函数,就对变量求导;如果是多元,就对变量微分。
多元函数二阶求导
为方便起见,做出如下定义:有z=f(u,v)。f1’(u,v)=fu(u,v)——f对u求偏导;f2’=fv(u,v)——f对v求偏导;f12’’(u,v)=fuv(u,v)等等…
先求一阶偏导,再根据公式求二阶偏导数。需要注意的是此处求出来的是一阶偏导对变量的微分。由于一阶偏导内涵中间变量u、v,因此要再进行微分将一阶偏导对变量的微分变成二阶偏导。
隐函数求导
方程组
在求解的时候可以把行列式右边的常数和所求的变量前的系数代换,利用行列式法则求解。
以下给出例题