文章目录
m i n i m i z e f 0 ( x ) minimize\ \ \ f_0(x) minimize f0(x)
s u b j e c t t o f i ( x ) ≤ b i , i = 1 , . . . , m subject\ to\ \ \ f_i(x)\le b_i, i = 1,...,m subject to fi(x)≤bi,i=1,...,m
凸优化问题:
f
i
(
α
x
+
β
y
)
≤
α
f
i
(
x
)
+
β
f
i
(
y
)
,
x
,
y
∈
R
n
,
α
+
β
=
1
,
α
≥
0
,
β
≥
0
f_i(\alpha x+\beta y) \le \alpha f_i(x)+\beta f_i(y), \ x,y\in R^n, \alpha +\beta = 1,\alpha \ge 0,\beta\ge 0
fi(αx+βy)≤αfi(x)+βfi(y), x,y∈Rn,α+β=1,α≥0,β≥0
所有的函数都是凸函数时这个规划问题成为凸优化问题。
最小二乘问题
无约束条件下
m
i
n
i
m
i
z
e
∣
∣
A
x
−
b
∣
∣
2
2
minimize ||Ax-b||_2^2
minimize∣∣Ax−b∣∣22
A
T
A
x
=
A
T
b
A^TAx = A^Tb
ATAx=ATb
x
=
(
A
T
A
)
−
1
A
T
b
x = (A^TA)^{-1}A^Tb
x=(ATA)−1ATb
A
∈
R
k
×
n
,
k
≥
n
A\in R^{k\times n},k\ge n
A∈Rk×n,k≥n
此处可以猜想一下,举例如k个点拟合一条直线。k个方程求解n个自变量。
带权的最小二乘
Σ
w
i
(
a
i
T
x
−
b
)
\Sigma w_i(a_i^Tx-b)
Σwi(aiTx−b)
regularization
Σ
i
=
1
k
(
a
i
T
x
−
b
i
)
2
+
ρ
Σ
i
=
1
n
x
i
2
\Sigma_{i=1}^k(a_i^Tx-b_i)^2 + \rho \Sigma_{i=1}^n x_i^2
Σi=1k(aiTx−bi)2+ρΣi=1nxi2
线性规划
切比雪夫近似问题
m
i
n
i
m
i
z
e
m
a
x
i
=
1...
k
∣
a
i
T
x
−
b
i
∣
minimize\ max_{i=1...k}\ |a_i^Tx-b_i|
minimize maxi=1...k ∣aiTx−bi∣
与最小二乘不同,不使用平方而是使用极大值——一阶矩?1范数
不可微
转化为
m
i
n
i
m
i
z
e
t
minimize\ t
minimize t
s
u
b
j
e
c
t
t
o
a
i
T
x
−
t
≤
b
i
,
−
a
i
T
x
−
t
≤
−
b
i
subject\ to\ a_i^Tx-t\le b_i,-a_i^Tx-t\le-b_i
subject to aiTx−t≤bi,−aiTx−t≤−bi
内点法?
仿射
仿射集合:一个集合 C 在一个向量空间中被称为仿射集合,如果对于集合 CC 中的任意两个点 x 和 y,以及任意实数 α,其中 0≤α≤1,集合 CC 都包含点 (1−α)x+αy。
线性方程组的解集是一个仿射集合
A
x
=
b
Ax=b
Ax=b的解
x
1
≠
x
2
x_1\not=x_2
x1=x2
A
x
1
=
b
,
A
x
2
=
b
Ax_1=b,Ax_2=b
Ax1=b,Ax2=b
A
(
α
x
1
+
β
x
2
)
=
A
(
α
x
1
)
+
A
(
β
x
2
)
=
(
α
+
β
)
b
=
b
A(\alpha x_1 +\beta x_2) =A(\alpha x_1)+A(\beta x_2)= (\alpha+\beta)b = b
A(αx1+βx2)=A(αx1)+A(βx2)=(α+β)b=b
affine hull
The set of all affine combinations of points in some set C ⊆ Rn is called the affine hull of C, and denoted aff C
在欧几里得空间 Rn 中,一个集合 C 的仿射包(affine hull)是指所有包含在集合 C 中的点的仿射组合的集合。换句话说,它是通过 C中任意有限个点 x1,x2,…,xk的所有可能的线性组合的集合。
仿射包的理解?
aff C = { θ 1 x 1 + . . . + θ n x n ∣ x k ∈ C , Σ θ i = 1 } \textbf{aff}\ C = \{\theta_1x_1+...+\theta_nx_n |x_k\in C,\Sigma\theta_i=1 \} aff C={θ1x1+...+θnxn∣xk∈C,Σθi=1}
affine dimension
集合C的仿射维度定义为他的仿射包(?)
例:对单位圆上的点
{
x
∈
R
2
∣
x
1
2
+
x
2
2
=
1
}
\{x\in R^2|x_1^2+x_2^2 = 1 \}
{x∈R2∣x12+x22=1}
其仿射包是
R
2
R^2
R2(单位圆上的点通过线性组合可以产生)
相对内部(relative interior)
r
e
l
i
n
t
C
=
{
x
∈
C
∣
B
(
x
,
r
)
∩
aff
C
⊆
C
f
o
r
s
o
m
e
r
>
0
}
relint\ C = \{x\in C|B(x,r)\cap\textbf{aff}C\subseteq C\ for\ some\ r > 0\}
relint C={x∈C∣B(x,r)∩affC⊆C for some r>0}
就是这些点的邻域与aff C的交集仍然在C中。
c
l
C
r
e
l
i
n
t
C
cl\ C \\ \ relint\ C
cl C relint C 为边界
三维空间中的正方形
C
=
{
x
∈
R
3
∣
∣
x
1
∣
≤
1
,
∣
x
2
∣
≤
2
,
x
3
=
0
}
C = \{x\in R^3||x_1|\le1,|x_2|\le2,x_3 = 0\}
C={x∈R3∣∣x1∣≤1,∣x2∣≤2,x3=0}
其仿射包是什么呢?是由平面上的点组成的所有线性组合,那么自然是整个平面。那么dimension应该是2
凸集
x
1
∈
C
,
x
2
∈
C
,
0
≤
θ
≤
1
,
θ
x
1
+
(
1
−
θ
)
x
2
∈
C
x_1\in C,x_2\in C,0\le\theta\le1,\theta x_1+(1-\theta)x_2\in C
x1∈C,x2∈C,0≤θ≤1,θx1+(1−θ)x2∈C
则为凸集
仿射集都是凸集
凸组合:
θ
1
x
1
+
θ
2
x
2
+
.
.
.
+
θ
n
x
n
,
θ
i
≥
0
\theta_1 x_1+\theta_2x_2+...+\theta_nx_n,\theta_i\ge0
θ1x1+θ2x2+...+θnxn,θi≥0
凸包:
conv
C
=
{
θ
1
x
1
+
.
.
.
+
θ
k
x
k
∣
x
i
∈
C
,
θ
i
≥
0
,
i
=
1
,
.
.
.
,
k
,
θ
1
+
.
.
.
+
θ
k
=
1
}
\textbf{conv} C = \{\theta_1x_1+...+\theta_kx_k|x_i\in C,\theta_i\ge 0,i=1,...,k,\theta_1+...+\theta_k = 1\}
convC={θ1x1+...+θkxk∣xi∈C,θi≥0,i=1,...,k,θ1+...+θk=1}
设 CC 是一个集合,那么 CC 的凸包 conv©conv© 是包含 CC 中所有点的最小凸集合。换句话说,conv©conv© 是包含 CC 的所有点的最小凸集合,且没有其他凸集合包含 CC 中的所有点。
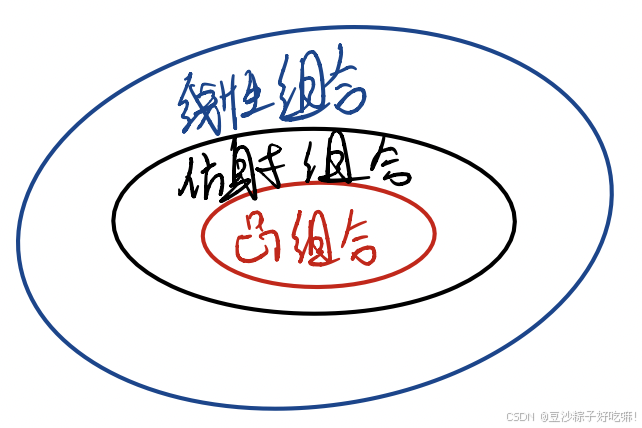
线性组合、仿射组合与凸组合
对比一下,都是
θ
1
x
1
+
.
.
.
+
θ
k
x
k
\theta_1x_1+...+\theta_kx_k
θ1x1+...+θkxk
但是线性组合对
θ
i
\theta_i
θi无要求,仿射要求
Σ
θ
i
=
1
\Sigma\theta_i=1
Σθi=1,凸组合要求
Σ
θ
i
=
1
\Sigma\theta_i=1
Σθi=1,且
θ
i
≥
0
\theta_i\ge 0
θi≥0
条件越来越强。
![./凸优化问题/凸优化笔记-基本概念/
锥集
对任意
x
∈
C
x\in C
x∈C,都有
θ
x
∈
C
\theta x\in C
θx∈C
锥的顶点在原点。
凸锥====== 又凸又锥(比如一个立在原点的在最粗的地方切开的洋葱头?)
θ
1
x
1
+
.
.
.
+
θ
k
x
k
,
θ
i
≥
0
\theta_1x_1+...+\theta_kx_k,\theta_i\ge 0
θ1x1+...+θkxk,θi≥0
conic combination
锥组合
锥包
{
θ
1
x
1
+
.
.
.
+
θ
k
x
k
∣
x
i
∈
C
,
θ
i
≥
0
,
i
=
1
,
.
.
.
,
k
}
\{\theta_1x_1+...+\theta_kx_k|x_i\in C,\theta_i\ge 0,i=1,...,k\}
{θ1x1+...+θkxk∣xi∈C,θi≥0,i=1,...,k}
C的锥包是能包含C的最小的锥集
![./凸优化问题/凸优化笔记-基本概念/
超平面和半空间
超平面
a
T
x
=
b
a^Tx = b
aTx=b
半空间
{
x
∣
a
T
x
≥
b
}
\{x|a^Tx\ge b\}
{x∣aTx≥b}
椭球
ϵ
=
{
x
∣
(
x
−
x
c
)
T
P
−
1
(
x
−
x
c
)
≤
1
}
\epsilon = \{x|(x-x_c)^TP^{-1}(x-x_c)\le 1\}
ϵ={x∣(x−xc)TP−1(x−xc)≤1}
P是对称且正定的,对称轴的长度由特征值的根号给出
λ
i
\sqrt{\lambda_i}
λi
多面体
P
=
{
x
∣
A
x
≼
b
,
C
x
=
d
}
P=\{x|Ax≼ b,Cx = d\}
P={x∣Ax≼b,Cx=d}
A
=
[
a
1
T
.
.
.
a
m
T
]
,
C
=
[
c
1
T
.
.
.
c
p
T
]
A = \begin{bmatrix}a_1^T\\.\\.\\.\\a_m^T\end{bmatrix},C = \begin{bmatrix}c_1^T\\.\\.\\.\\c_p^T\end{bmatrix}
A=
a1T...amT
,C=
c1T...cpT
单纯形
n维单纯形有n+1个顶点,如1维线段,2维三角形,三维四面体
单位单纯形
x
⪰
0
,
1
T
x
≤
1
x\succeq0,\textbf 1^Tx\le1
x⪰0,1Tx≤1 , n维度
概率单纯形
x
⪰
0
,
1
T
x
=
1
x\succeq 0,\textbf 1^Tx=1
x⪰0,1Tx=1, n-1维度
整半定锥
对称矩阵集合
S
n
=
{
X
∈
R
n
×
n
∣
X
=
X
T
}
S^n=\{X\in R^{n\times n}|X=X^T\}
Sn={X∈Rn×n∣X=XT}
其维度为
(
n
+
1
)
n
/
2
(n+1)n/2
(n+1)n/2,可以想想有多少个独立的元素。
非负
S
+
n
=
{
X
∈
R
n
×
n
∣
X
=
X
T
,
X
⪰
0
}
S^n_+=\{X\in R^{n\times n}|X=X^T,X\succeq0\}
S+n={X∈Rn×n∣X=XT,X⪰0}
正
S
+
n
+
=
{
X
∈
R
n
×
n
∣
X
=
X
T
,
X
≻
0
}
S^n_++=\{X\in R^{n\times n}|X=X^T,X\succ 0\}
S+n+={X∈Rn×n∣X=XT,X≻0}
convex set:都是
convex cone:
S
+
n
+
S^n_++
S+n+不是,因为没有0
保凸性的操作
仿射变换、凸集的交集、求和、笛卡尔内积
设有线性矩阵不等式(LMI)
A
(
x
)
=
x
1
A
1
+
.
.
.
+
x
n
A
n
⪯
B
A(x)=x_1A_1+...+x_nA_n\preceq B
A(x)=x1A1+...+xnAn⪯B
其解集是convex的
仿射变换呢?
透视函数
降低维度
P
:
R
n
+
1
→
R
n
P:R^{n+1}\to R^n
P:Rn+1→Rn
可以等效为一个小孔成像摄像机
接受平面位置在
x
3
=
−
1
x_3 = -1
x3=−1
小孔在原点,被测物
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3
则相点为
−
(
x
1
/
x
3
,
x
2
/
x
3
,
1
)
-(x_1/x_3,x_2/x_3,1)
−(x1/x3,x2/x3,1)
d
o
m
P
=
R
n
×
R
+
+
dom P = R^n\times R_{++}
domP=Rn×R++
P
(
z
,
t
)
=
z
/
t
P(z,t)=z/t
P(z,t)=z/t
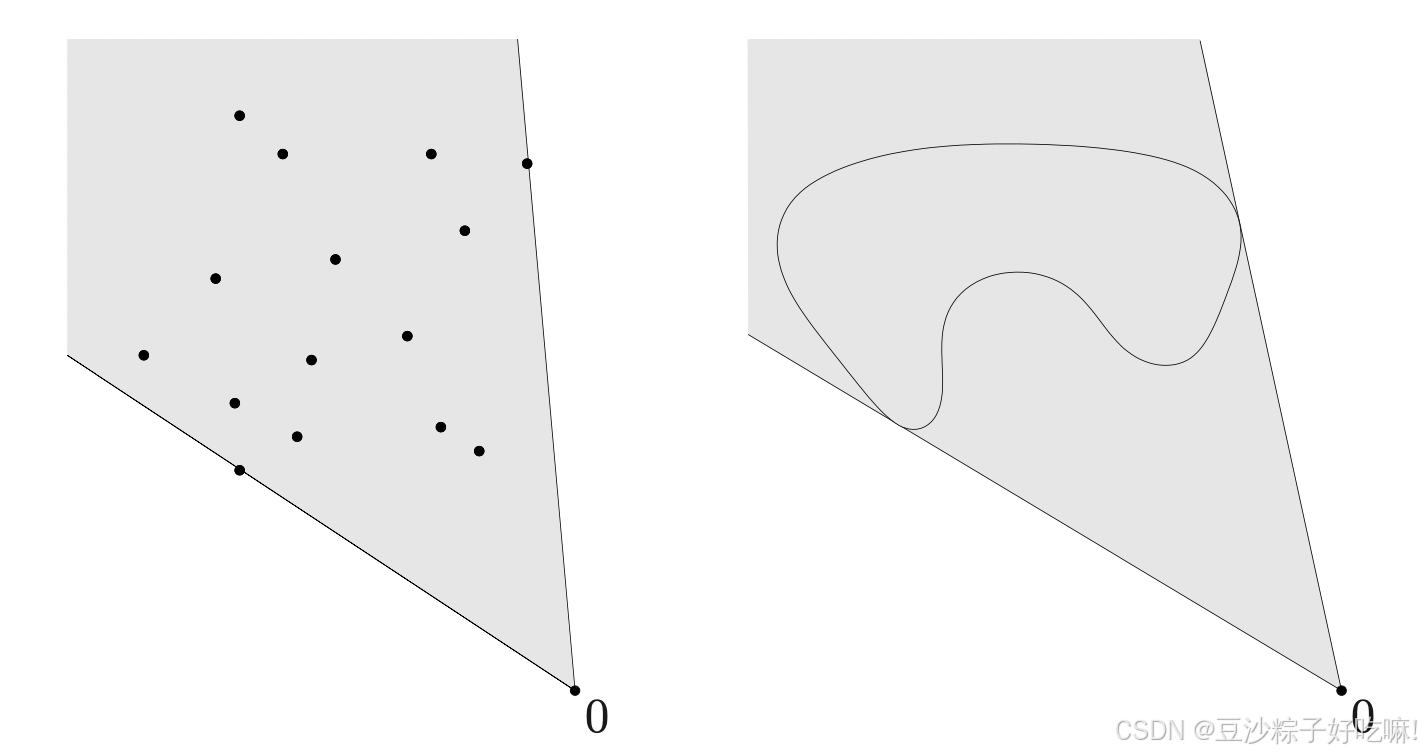
如果domP中的C是凸点,他的像
P
(
C
)
=
{
P
(
x
)
∣
x
∈
C
}
P(C)=\{P(x)|x\in C\}
P(C)={P(x)∣x∈C}
也是凸的
凸函数的条件
1阶判定条件
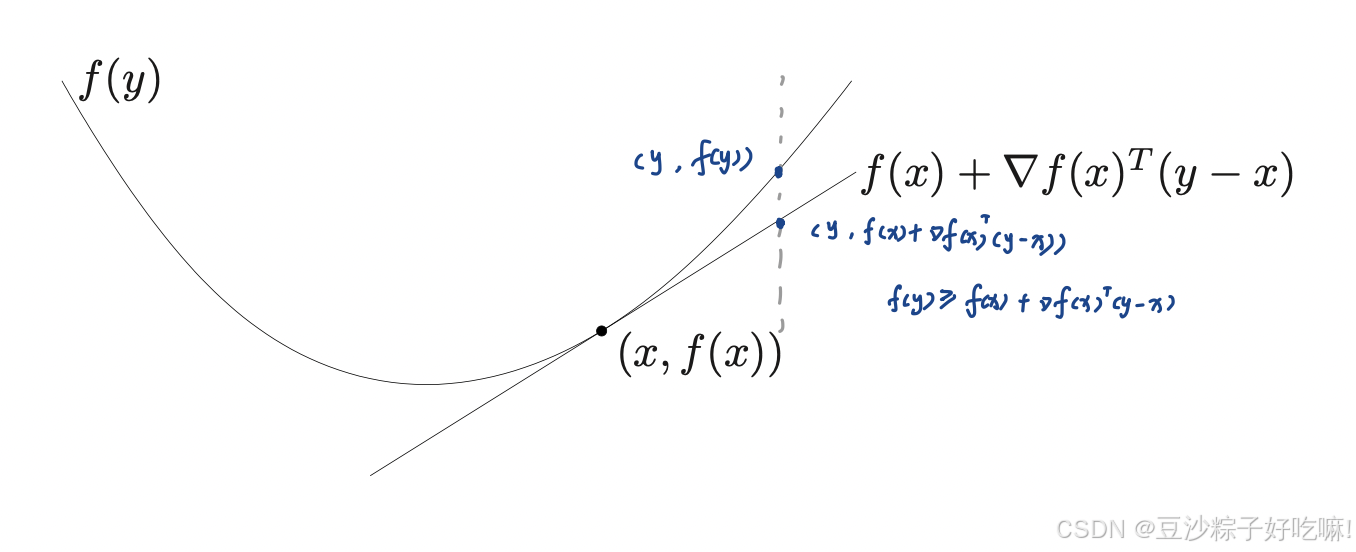
若f可微,当且仅当dom f凸,而且
f
(
y
)
≥
f
(
x
)
+
∇
f
(
x
)
T
(
y
−
x
)
f(y)\ge f(x)+\nabla f(x)^T(y-x)
f(y)≥f(x)+∇f(x)T(y−x)
![./凸优化问题/凸优化笔记-基本概念/
其几何意义为函数上的点永远比某一条切线上的点高(或重合)
(该形式为泰勒一阶展开)
2阶判定条件
∇ f ⪰ 0 \nabla f \succeq 0 ∇f⪰0
-
R
n
R^n
Rn上的范数都是凸的(由范数的三角不等式得到)
∣ ∣ u 1 ∣ ∣ + ∣ ∣ u 2 ∣ ∣ ≥ ∣ ∣ u 1 + u 2 ∣ ∣ ||u_1||+||u_2|| \ge ||u_1+u_2|| ∣∣u1∣∣+∣∣u2∣∣≥∣∣u1+u2∣∣ - 最大值函数是凸的
m a x ( x ) + m a x ( y ) > m a x ( x + y ) max(x) + max(y) >max(x+y) max(x)+max(y)>max(x+y) - 二次overlinear函数
f ( x , y ) = x 2 / y , y > 0 ∇ 2 f = [ 2 / y − 2 x / y 2 − 2 x / y 2 2 x 2 / y 3 ] , d e t ( ∇ 2 f ) = 2 y 3 ∣ y 2 − x y − x y 2 x 2 ∣ = 2 y 2 ∗ ( 2 x 2 y 2 − x 2 y 2 ) > 0 f(x,y) = x^2/y,y>0\ \ \ \ \ \ \nabla^2 f = \begin{bmatrix}2/y & -2x/y^2 \\-2x/y^2 & 2x^2/y^3\end{bmatrix}, det(\nabla^2 f) = \frac{2}{y^3}\begin{vmatrix}y^2&-xy\\-xy&2x^2\end{vmatrix}=\frac{2}{y^2}*(2x^2y^2-x^2y^2)>0 f(x,y)=x2/y,y>0 ∇2f=[2/y−2x/y2−2x/y22x2/y3],det(∇2f)=y32 y2−xy−xy2x2 =y22∗(2x2y2−x2y2)>0 - 对数求和指数
f ( x ) = log ( e x p ( x 1 ) + e x p ( x 2 ) + . . . + e x p ( x n ) ) f(x) = \log(exp(x_1)+exp(x_2)+...+exp(x_n)) f(x)=log(exp(x1)+exp(x2)+...+exp(xn))
∂ f ∂ x i = exp ( x i ) Σ j = 0 j = n exp ( x j ) \frac{\partial f}{\partial x_i} = \frac{\exp(x_i)}{\Sigma_{j =0} ^{j=n} \exp(x_j)} ∂xi∂f=Σj=0j=nexp(xj)exp(xi)
z = ( e x p ( x 1 ) , e x p ( x 2 ) , . . . , e x p ( x n ) ) , Σ j = 0 j = n exp ( x j ) = 1 T z z = (exp(x_1),exp(x_2),...,exp(x_n)),\ \Sigma_{j =0} ^{j=n} \exp(x_j)= \textbf{1}^Tz z=(exp(x1),exp(x2),...,exp(xn)), Σj=0j=nexp(xj)=1Tz
求Hessian矩阵
∂ 2 f ∂ x i ∂ x j = − exp ( x i ) exp ( x j ) ( 1 T z ) 2 , i ≠ j \frac{\partial^2f}{\partial x_i\partial x_j}=-\frac{\exp(x_i)\exp(x_j)}{(\textbf{1}^Tz)^2},i\not = j ∂xi∂xj∂2f=−(1Tz)2exp(xi)exp(xj),i=j
∂ 2 f ∂ x i 2 = exp ( x i ) 1 T z − exp ( x i ) 2 ( 1 T z ) 2 \frac{\partial^2 f}{\partial x_i^2} = \frac{\exp(x_i)}{\textbf{1}^Tz} - \frac{\exp(x_i)^2}{(\textbf{1}^Tz)^2} ∂xi2∂2f=1Tzexp(xi)−(1Tz)2exp(xi)2
i=j时二阶导导前半部分可以组成一个对角阵列,后半部分和不等时的形式相同
∇ 2 f = 1 ( 1 T z ) 2 ( ( 1 T z ) d i a g ( z ) − z z T ) \nabla^2f=\frac{1}{(\textbf{1}^Tz)^2 } ((\textbf{1}^Tz )diag(z)-zz^T) ∇2f=(1Tz)21((1Tz)diag(z)−zzT)
对任意v,有
v T ∇ 2 f v = 1 ( 1 T z ) 2 ( Σ j = 0 j = n z j Σ j = 0 j = n v j 2 z j − v T z z T v ) = 1 ( 1 T z ) 2 ( Σ j = 0 j = n z j Σ j = 0 j = n v j 2 z j − ( Σ j = 0 j = n z j v j ) 2 ) v^T\nabla^2f\ v=\frac{1}{(\textbf{1}^Tz)^2 } (\Sigma_{j =0} ^{j=n} z_j \Sigma_{j =0} ^{j=n} v_j^2z_j-v^Tzz^Tv)= \frac{1}{(\textbf{1}^Tz)^2 } (\Sigma_{j =0} ^{j=n} z_j \Sigma_{j =0} ^{j=n} v_j^2z_j-(\Sigma_{j =0} ^{j=n}z_jv_j)^2) vT∇2f v=(1Tz)21(Σj=0j=nzjΣj=0j=nvj2zj−vTzzTv)=(1Tz)21(Σj=0j=nzjΣj=0j=nvj2zj−(Σj=0j=nzjvj)2)
此处使用Cauchy-Schwarz不等式, a i = v i z i , b i = z i , ( a T a ) ( b T b ) ≥ ( a T b ) 2 a_i = v_i\sqrt{z_i},b_i = \sqrt{z_i},(a^Ta) (b^Tb)\ge (a^Tb)^2 ai=vizi,bi=zi,(aTa)(bTb)≥(aTb)2,可得上式不小于0。
Epigraph 外图
函数f的graph定义为
{
(
x
,
f
(
x
)
)
∣
x
∈
dom
f
}
\{(x,f(x))|x\in \textbf{dom}\ f\}
{(x,f(x))∣x∈dom f}
是
R
n
+
1
\textbf{R}^{n+1}
Rn+1的子集
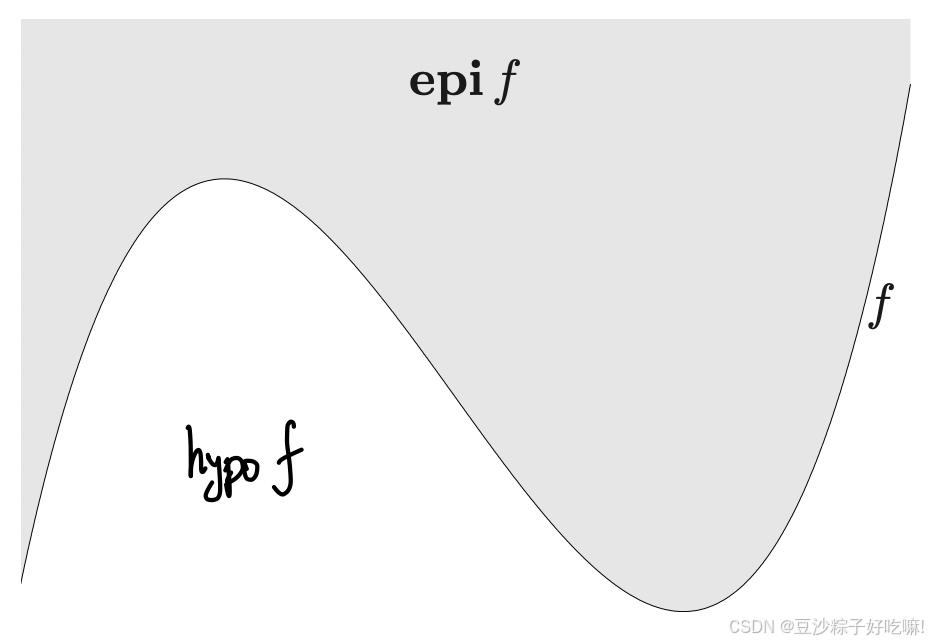
其epigraph为
epi
f
=
{
(
x
,
t
)
∣
x
∈
dom
f
,
f
≤
t
}
\textbf{epi}\ f=\{ (x,t) | x\in \textbf{dom} \ f,f\le t\}
epi f={(x,t)∣x∈dom f,f≤t}
(‘Epi’ means ‘above’ so epigraph means ‘above the graph’.)
亚图为
hypo
f
=
{
(
x
,
t
)
∣
x
∈
dom
f
,
f
≥
t
}
\textbf{hypo}f = \{ (x,t) | x\in \textbf{dom} \ f,f\ge t \}
hypof={(x,t)∣x∈dom f,f≥t}
这个图能建立凸集和凸函数的关系。当且仅当外图(epi f)是凸的时候函数是凸的。
当且仅当亚图(hypo f)是凸的时候函数是凹的
- 矩阵分式函数
f ( x , Y ) = x T Y − 1 x , dom f = R n × S + + n f(x,Y) = x^TY^{-1}x,\ \ \ \textbf{dom} \ f=\textbf{R}^n\times\textbf{S}^n_{++} f(x,Y)=xTY−1x, dom f=Rn×S++n
epi
f
=
{
(
x
,
Y
,
t
)
∣
Y
≻
0
,
f
(
x
,
Y
)
≤
t
}
\textbf{epi} f =\{(x,Y,t)|Y\succ0, f(x,Y)\le t \}
epif={(x,Y,t)∣Y≻0,f(x,Y)≤t}
x
T
Y
−
1
x
≤
t
x^TY^{-1}x\le t
xTY−1x≤t
此处需要用到舒尔补(Schur complement)
M
=
[
A
B
C
D
]
M = \begin{bmatrix}A&B\\C&D\end{bmatrix}
M=[ACBD]
如果A可逆,则其舒尔补为
D
−
C
A
−
1
B
D-CA^{-1}B
D−CA−1B
代入有
M
=
[
Y
x
x
T
t
]
⪰
0
M = \begin{bmatrix}Y&x\\x^T&t\end{bmatrix}\succeq 0
M=[YxTxt]⪰0