数据结构实验十二 图的遍历及应用

一、【实验目的】

1、 理解图的存储结构与基本操作；

2、熟悉图的深度度优先遍历和广度优先遍历算法

3、掌握图的单源最短路径算法

二、【实验内容】

1.根据下图（图见实验11）邻接矩阵，编程实现该图的深度与广度优先遍历算法，输出遍历序列。

2.单源节点最短路径问题

问题描述:求从有向图的某一结点出发到其余各结点的最短路径。

基本要求:

（1）有向图采用邻接矩阵表示。

（2）单源节点最短路径问题采用Dijkstra算法。

（3）输出有向图中从源结点T到其余各结点的最短路径和最短路径值。

三、实验源代码

//SequenceList.h

typedef struct
{
	ElemType list[MaxSize];
    int size;        
} SequenceList;

//顺序表初始化 
void ListInitialize(SequenceList *L)
{
    L->size = 0;
}

int ListLength(SequenceList L)
{
    return L.size;
}

//顺序表插入操作 
int ListInsert(SequenceList *L, int i, ElemType x)
{
    int j;
    if (L->size >= MaxSize)
    {
        printf("顺序表已满无法插入！\n");
        return 0;
    }
    else if (i < 0 || i > L->size)
    {
        printf("参数i不合法！\n");
        return 0;
    }
    else
    {
        for (j = L->size; j > i; j--)
        {
            L->list[j] = L->list[j-1];
        }
        L->list[i] = x;
        L->size++;
    }
    return 1;
}

int ListDelete(SequenceList *L, int i, ElemType *x)
{
    int j;
    if (L->size <= 0)
    {
        printf("顺序表已空无数据可删！\n");
        return 0;
    }
    else if (i < 0 || i > L->size-1)
    {
        printf("参数i不合法");
        return 0;
    }
    else
    {
        *x = L->list[i];
        for (j = i+1; j < L->size-1; j++) 
        {
            L->list[j-1] = L->list[j];
        }
        L->size--;
        return 1;
    }
}

int ListGet(SequenceList L, int i, ElemType *x)
{
    if (i < 0 || i > L.size-1)
    {
        printf("参数i不合法！\n");
        return 0;
    }
    else
    {
        *x = L.list[i];
        return 1;
    }
}

SequenceQueue.h
//定义循环队列结构体
typedef struct
{
	ElemType queue[MaxQueueSize];
	int rear;
	int front;
	int count;
 } SequenceQueue;

//初始化顺序循环队列 
void QueueInitiate(SequenceQueue *Q)
{
	Q->rear =0;
	Q->front=0;
	Q->count=0; 
}

//判空 
int QueueNotEmpty(SequenceQueue Q)
{
	if(Q.count ==0)
	{
		return 0;
	}
	else
	{
		return 1;
	}
}

//入队 
int QueueAppend(SequenceQueue *Q,ElemType x)
{
	if(Q->count>0&&Q->front==(Q->front+Q->count)%40)
	{
		printf("队列已满无法插入！\n");
		return 0;
	}
	else
	{
		Q->queue[Q->rear] = x;
		Q->rear=(Q->rear+1)%MaxQueueSize;
		Q->count ++;
		
		return 1;
	}
}

//出队 
int QueueDelete(SequenceQueue *Q,int *d)
{
	if(Q->count==0)
	{
		printf("循环队列已空无数据元素出队列！\n");
		return 0;
	}
	else
	{
		*d=Q->queue[Q->front];
		Q->front=(Q->front+1)%MaxQueueSize;
		Q->count--;
		return 1;
	}
}

//12.c
#include<stdio.h>
#include<stdlib.h>
#define MaxSize 100
#define MaxVertices 10
#define MaxEdges 100
#define MaxWeight 10000

#define MaxQueueSize 10

typedef char ElemType;

#include"SequenceList.h" 

typedef struct
{
	SequenceList Vertices;
	int edge[MaxVertices][MaxVertices];
	int numOfEdges;
}MatrixGraph;



typedef struct 
{
	int row;
	int col;
	int weight;
}RCW;

//初始化 
void Initiate(MatrixGraph *G,int n)
{
	int i,j;
	for(i=0;i<n;i++)
	{
		for(j=0;j<n;j++)
		{
			if(i==j)
			{
				G->edge[i][j]=0;
			}
			else
			{
				G->edge[i][j]=MaxWeight;
			}
		}
	}
	G->numOfEdges=0;//边的条数置为0 
	ListInitialize(&G->Vertices);//顺序表初始化 
}

//插入顶点
void InsertVertex(MatrixGraph *G,ElemType vertex)
{
	ListInsert(&G->Vertices,G->Vertices.size,vertex);// 
 } 
 
 //插入边 
 void InsertEdge(MatrixGraph *G,int v1,int v2,int weight)
 {
 	if(v1<0||v1>G->Vertices.size||v2<0||v2>G->Vertices.size)
	{
	 	printf("参数v1或参数v2越界出错！\n");
		return; 
	} 
	G->edge[v1][v2]=weight;
	G->numOfEdges++;
 }

void CreatGraph(MatrixGraph *G,ElemType V[],int n,RCW E[],int e)
{
	int i,k;
	Initiate(G,n);
	for(i=0;i<n;i++)
	{
		InsertVertex(G,V[i]);
	}
	for(k=0;k<e;k++)
	{
		InsertEdge(G,E[k].row,E[k].col,E[k].weight);
	 } 
}

//取第一个邻接顶点
int GetFirstVex(MatrixGraph G,int v,int visited[])
{
	int col;
	if(v<0||v>G.Vertices.size)
	{
		printf("参数v1越界出错！\n");
		return -1;
	}
	for(col=0;col<=G.Vertices.size;col++)
	{
		if(!visited[col])
			if(G.edge[v][col]>0&&G.edge[v][col]<MaxWeight)
			{

				return col;
			}
	}
	return -1;
 } 
 
 //取下一个邻接顶点
 int GetNextVex(MatrixGraph G,int v1,int v2,int visited[])
 {
 	int col;

 	if(v1<0||v1>G.Vertices.size||v2<0||v2>G.Vertices.size)
 	{
 		printf("参数v1或v2越界出错！\n");
 		return -1;
	 }
	 for(col=v2+1;col<=G.Vertices.size;col++)
	 {
		if(!visited[col])
		{
			if(G.edge[v1][col]>0&&G.edge[v1][col]<MaxWeight)
	 		{
	 		return col;
		 	}
		 	
		}
	 }
	 return -1;
  } 

//深度优先遍历
void DepthFSearch(MatrixGraph G,int v,int visited[])
{
	int w;
	printf("%c ",G.Vertices.list[v]);
	visited[v]=1;
	w=GetFirstVex(G,v,visited);
	while(w!=-1) 
	{
		if(!visited[w])
			DepthFSearch(G,w,visited);
		w=GetNextVex(G,v,w,visited);
	}
 } 
 
 //引用顺序队列头文件 
 #include"SequenceQueue.h"
 
 //取第一个邻接顶点
int GetFirstVex2(MatrixGraph G,int v,int visited[])
{
	int col;
	if(v<0||v>G.Vertices.size)
	{
		printf("参数v1越界出错！\n");
		return -1;
	}
	for(col=0;col<=G.Vertices.size;col++)
	{
			if(G.edge[v][col]>0&&G.edge[v][col]<MaxWeight)
			{

				return col;
			}
	}
	return -1;
 } 
 
 //广度优先遍历
 void BroadFSearch(MatrixGraph G,int v,int visited2[])
 {
 	int u,w;
 	SequenceQueue queue;
 	printf("%c ",G.Vertices.list[v]);
 	visited2[v]=1;
 	QueueInitiate(&queue);
 	QueueAppend(&queue,v);
 	while(QueueNotEmpty(queue))
 	{
 		QueueDelete(&queue,&u);//传地址？ 
 
 		w=GetFirstVex2(G,u,visited2);
 		while(w!=-1)
 		{
 			if(!visited2[w])
 			{
 				printf("%c ",G.Vertices.list[w]);
 				visited2[w]=1;
 				QueueAppend(&queue,w);
			 }
			 w=GetNextVex(G,u,w,visited2);
		 }
	 }
  } 
  
//狄克斯特拉算法找最短路径
//带权图G从下标v0顶点到其他顶点的最短距离distance
//和最短路径下标path 
void Dijkstra(MatrixGraph G,int v0,int distance[],int path[]) 
{ 
	int n=G.Vertices.size;
	int *s=(int*)malloc(sizeof(int)*n);
	int minDis,i,j,u;
	for(i=0;i<n;i++)//初始化
	{
		distance[i]=G.edge[v0][i];
		s[i]=0;
		if(i!=v0&&distance[i]<MaxWeight)
			path[i]=v0;
		else
			path[i]=-1;
	 } 
	 s[v0]=1;
	 for(i=1;i<n;i++)
	 {
	 	minDis=MaxWeight;
	 	for(j=0;j<=n;j++)//在还未找到最短路径的顶点集中选有最短距离的顶点u 
	 	{
	 		if(s[j]==0&&distance[j]<minDis)
	 		{
	 			u=j;
	 			minDis=distance[j];
			 }
		 }
		if(minDis==MaxWeight)//当已不存在路径时算法结束 
			return;
		s[u]=1;//标记顶点u已从集合T加入到集合S中 
		for(j=0;j<n;j++)//修改从v0到其他顶点的最短距离和最短路径 
		{
			if(s[j]==0&&G.edge[u][j]<MaxWeight&&distance[u]+G.edge[u][j]<distance[j])
			{
				distance[j]=distance[u]+G.edge[u][j];
				path[j]=u;
			 } 
		 } 
	 }
}

//正序输出最短路径
printfpath(MatrixGraph g1,int path[])
{
	char path2[6];
	int i,j,k;
	for(i=1;i<6;i++)
	{
		printf("\n");
		j=i;
		k=0;
		while(j!=-1)
		{
			path2[k]=g1.Vertices.list[j];
			k++;
			j=path[j];	
		}
		k--;
		printf("%c",path2[k]);
		while(k>0)
		{
			k--;
			printf("->%c",path2[k]);
		}
	 } 
 } 

void main(void)
{
	MatrixGraph g1;
	ElemType a[]={'A','B','C','D','E','F'};
	RCW rcw[]={{0,2,5},{0,3,30},{1,0,2},{1,4,8},{2,1,15},{2,5,7},{4,3,4},{5,3,10},{5,4,18}};
	int n=6,e=9;
	int i,j;
	CreatGraph(&g1,a,n,rcw,e);
	printf("顶点集合为：");
	for(i=0;i<g1.Vertices.size;i++)
	{
		printf("%c  ",g1.Vertices.list[i]);
	 } 
	 printf("\n");
	 printf("邻接矩阵为：\n");
	 for(i=0;i<g1.Vertices.size;i++)
	 {
	 	for(j=0;j<g1.Vertices.size;j++)
	 	{
	 		printf("%5d  ",g1.edge[i][j]);
		}
		printf("\n");
	 }
	printf("深度优先遍历结果为："); 
	int visited[6]={};
	DepthFSearch(g1,0,visited);
	printf("\n");
	int visited2[6]={};
	printf("广度优先遍历结果为：");
	BroadFSearch(g1,0,visited2); 
	printf("\n");
	printf("源结点T到其余各结点的最短路径为：");
	int distance[6];
	int path[6]={-1};
	Dijkstra(g1,0,distance,path);
	printfpath(g1,path);
	printf("\n");
	printf("源结点T到其余各结点的最短路径值为：");
	for(i=0;i<n;i++)
	{
		printf("\n%c->%c:",g1.Vertices.list[0],g1.Vertices.list[i]);
		printf("%d",distance[i]);
	}
}

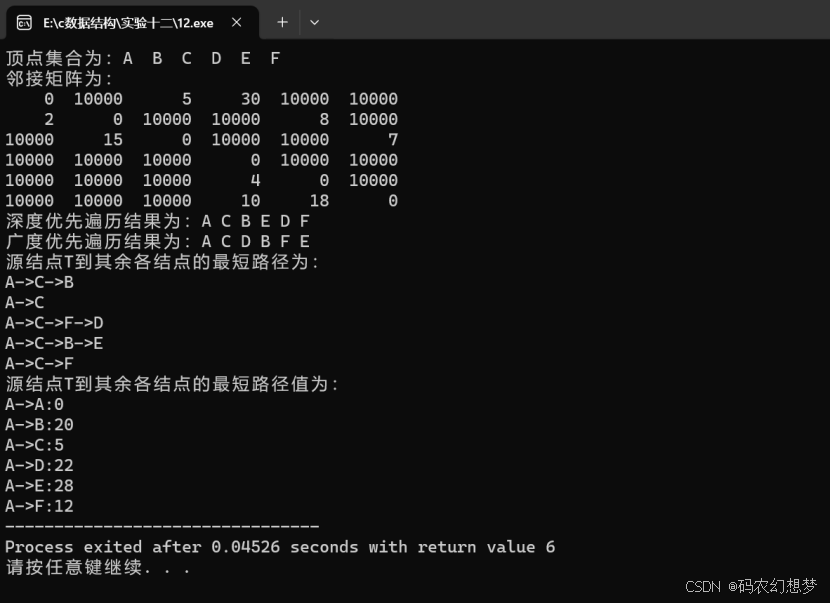
四、实验结果

五、实验总结
总结狄克斯特拉算法：
首先，使用 malloc 分配了一个大小为 n 的整型数组 s，用于标记顶点是否已经加入集合 S 中。
然后进行了初始化，初始化了距离数组 distance 和标记数组 s，以及路径数组 path。初始化时，将源顶点 v0 到其他顶点的距离和路径进行了设置。
接下来使用一个循环来依次将未加入集合 S 中的顶点加入，并更新最短路径和最短距离。在每次循环中，首先找到未加入集合 S 中且距离最短的顶点 u，然后将其标记为已加入集合 S 中。
在找到顶点 u 后，再次遍历所有未加入集合 S 中的顶点，更新从源顶点 v0 到其他顶点的最短距离和最短路径。如果通过顶点 u 可以找到更短的路径，就更新距离数组 distance 和路径数组 path。
最终得到的 distance 数组中存储了从源顶点 v0 到各顶点的最短距离，path 数组中存储了相应的最短路径。