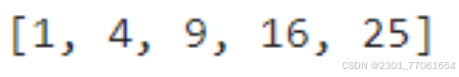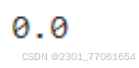数据的分布和映射

一、数据的分布

数据分布描述了数据在不同取值区间的散布情况，它可以帮助我们了解数据的集中程度、离散程度、对称性等重要特征。这些信息对于数据清洗、特征选择、模型构建等数据处理和分析环节至关重要。常见的数据分布包括均匀分布、泊松分布、正态分布等。

1.1均匀分布

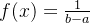
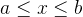
均匀分布表示数据点在一个固定范围内均匀分布，每个数据点的概率相等。连续的均匀分布密度函数为 $f(x)=\frac{{1}}{b-a}$ ，且 $a\leq x\leq b$ 。在python中可以使用NumPy库的 numpy.random.uniform函数生成均匀分布的随机数。例如，要生成 10 个介于 1和 7之间的离散均匀分布随机数，可以使用以下代码：

import numpy as np
# 生成离散均匀分布随机数
random_numbers = np.random.randint(1, 7, 10)
print(random_numbers)

结果：

1.2泊松分布

泊松分布泊松分布描述在固定时间段或空间内，事件发生的次数。泊松分布的概率质量函数为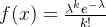 $f(x)=\frac{\lambda ^{k }e^{-\lambda }}{k!}$ ,其中是x随机变量，表示事件发生的次数；k是事件发生的具体次数； $\lambda$ 是单位时间或空间内事件发生的平均次数，e是自然常数。泊松分布的均值和方差都等于 $\lambda$ 。在python中使用NumPy库中的numpy.random.poisson函数可以生成泊松分布的随机数。要生成 10 个 $\lambda$ 参数为3的泊松分布随机数，可以使用以下代码：


import numpy as np

# 生成泊松分布随机数
random_numbers = np.random.poisson(3, 10)
print(random_numbers)

结果：

1.3正态分布

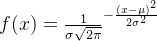
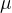
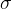
正态分布是一种常见的数据分布，数据点在一个固定范围内遵循正态分布。正态分布的图像呈钟形，具有对称性。其概率密度函数为 $f(x)=\frac{1}{\sigma \sqrt{2\pi }}^{-\frac{(x-\mu)^{2} }{2\sigma ^{2}}}$ 其中 $\mu$ 是均值。 $\sigma$ 是标准差，决定了分布的离散程度。使用NumPy的 numpy.random.normal 函数可以生成正态分布的随机数。例如，生成 100 个均值为0，标准差为1的正态分布随机数，可以使用以下代码

import numpy as np

random_numbers = np.random.normal(0, 1, 10)
print(random_numbers)

结果：

python中的数据分布除了上面三个例子还有很多，例如指数分布可以使用np.random.exponential二项分布：numpy.random.binomial；几何分布：numpy.random.geometric。

1.4python中数据可视化的数据分布

数据分布的可视化数据可视化是展示数据分布的重要手段，其能够更加直观理解数据。可以使用Python的matplotlib和seaborn库进行绘制，如直方图、箱线图和核密度图等。以正太分布为例。

绘制正态分布概率密度函数图像和直方图

from scipy.stats import binom
import matplotlib.pyplot as plt
import numpy as np

# 正态分布的参数
mu = 0  # 均值
sigma = 1  # 标准差

# 生成用于绘制概率密度函数图像的x值（在一个合适的区间内）
x = np.linspace(mu - 3 * sigma, mu + 3 * sigma, 100)

# 计算对应的概率密度函数值
y = norm.pdf(x, loc=mu, scale=sigma)

# 绘制正态分布概率密度函数曲线
plt.plot(x, y, label='正态分布概率密度函数', color='blue')

# 生成一定数量的正态分布随机数（这里生成1000个）
random_numbers = np.random.normal(mu, sigma, 1000)

# 绘制随机数的直方图（用于对比实际抽样分布情况）
plt.hist(random_numbers, bins=30, density=True, alpha=0.5, label='随机数直方图', color='orange')

# 添加标题、坐标轴标签和图例
plt.title('正态分布图像')
plt.xlabel('X')
plt.ylabel('概率密度')
plt.legend()

# 显示图形
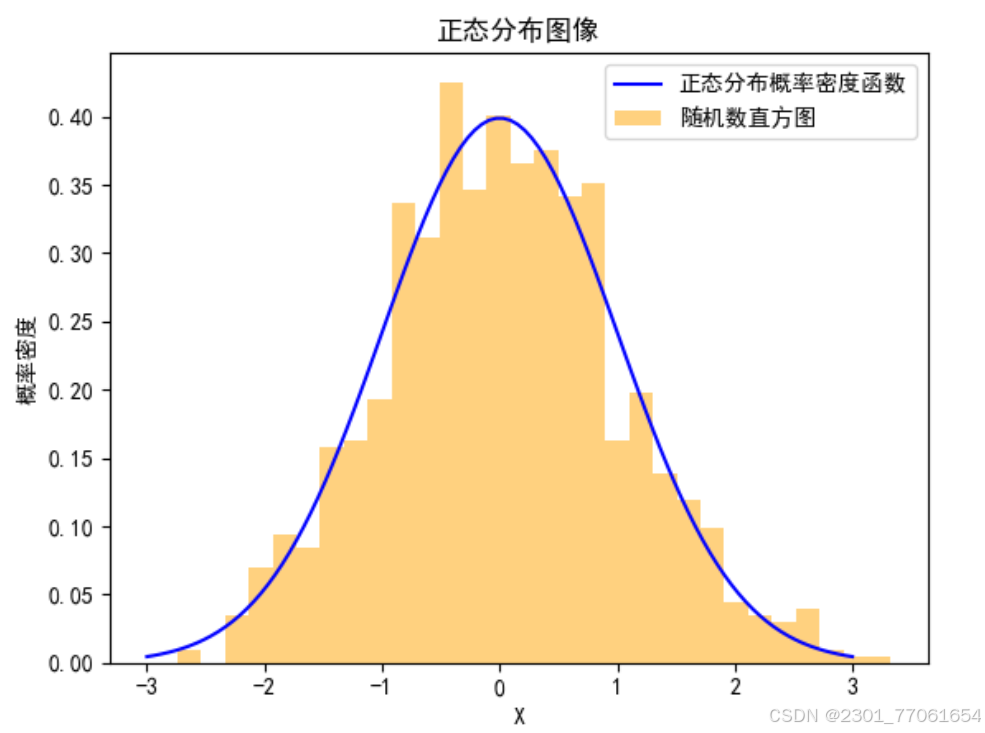
plt.show()

正太分布概率密度函数图如图所示：

生成了一个标准的正态分布图。图中的蓝色曲线是正态分布概率密度函数曲线。黄色柱状图代表随机数直方图。 x = 0 处达到峰值。图像的标题是 “正态分布概率密度函数图像”。在正态分布中，横轴通常表示随机变量的值，其范围从 -3 到 3。纵轴为 “概率密度”，其范围从 0.00 到 0.40。

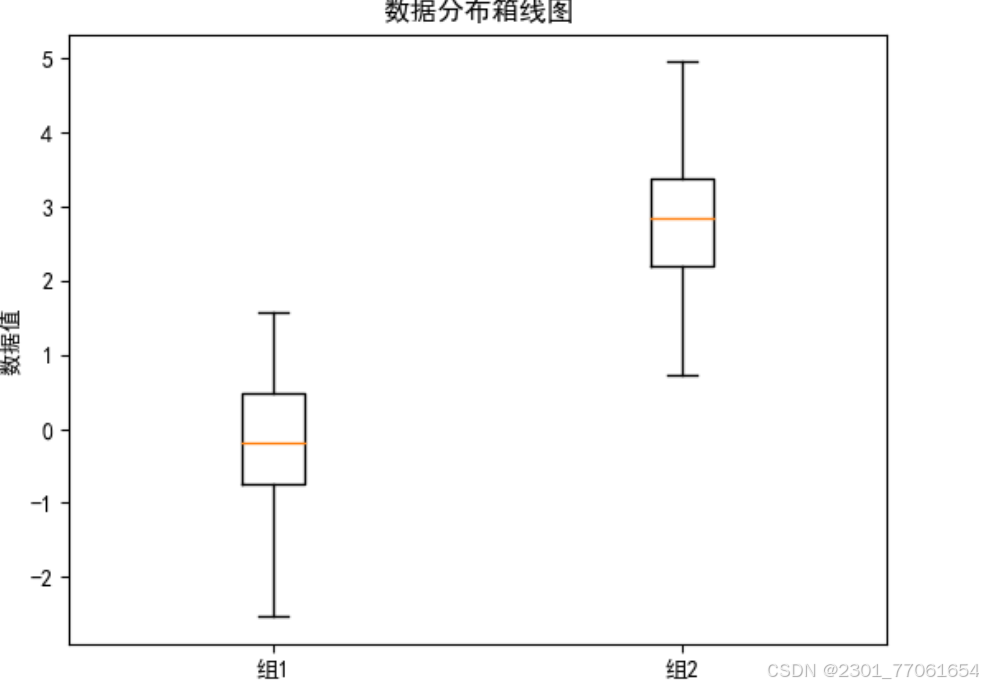
箱线图能够展示数据的多个关键统计信息，包括中位数、下四分位数、上四分位数、最小值和最大值。箱线图的箱体部分表示中间 50% 的数据范围，箱体内的线条表示中位数。

   import matplotlib.pyplot as plt
   import numpy as np

   # 生成两组随机数据（以正态分布为例）
   data1 = np.random.normal(0, 1, 100)
   data2 = np.random.normal(3, 1, 100)
   data = [data1, data2]
   plt.boxplot(data)
   plt.xticks([1, 2], ['组1', '组2'])
   plt.ylabel('数据值')
   plt.title('数据分布箱线图')
   plt.show()

二、数据映射

在Python中，数据映射是一个重要的概念，它涉及到将一种数据结构或形式转换为另一种数据结构或形式的过程。以下是一些关于Python数据映射的详细介绍：

2.1 使用字典实现映射

字典是Python中用于存储键值对的数据结构，由键（key）和值（value）组成，可以快速查找、插入和删除元素。通过字典，可以实现数据的映射。例如，可以将字符串映射到数字或其他类型的值上。

my_dict = {
    "name": "Alice",
    "age": 25,
    "city": "New York"
}

结果：

2.2 使用函数实现映射

Python中的 map() 函数可以将一个函数应用于一个可迭代对象中的每个元素，并返回一个迭代器。这可以用来实现数据的映射

def square(x):
    return x ** 2

numbers = [1, 2, 3, 4, 5]
squared_numbers = map(square, numbers)
print(list(squared_numbers))

结果：

2.3使用 lambda 表达式

表达式 lambda 表达式提供了一种简洁的方式来创建匿名函数，常与 map 函数结合使用，实现数据映射。

numbers = [1, 2, 3, 4, 5]
squared_numbers = map(lambda x: x ** 2, numbers)
print(list(squared_numbers))

结果：

2.4Pandas中的映射

Pandas是Python中非常流行的数据处理和分析库，提供了很多方便易用的数据转换和映射功能。 map() 方法是Pandas中用于数据映射的一个常用方法，它允许对Series或DataFrame中的一列进行映射转换。

# 读入数据文件
data = pd.read_csv('data.csv')

# 编码映射
map_dict = {'female': 0, 'male': 1}  # 字典映射
data['sex'] = data['sex'].map(map_dict)

结果

2.5ChainMap

Python中的 collections 模块提供了 ChainMap 类，它是一种将多个字典作为一个单元管理在一起的数据结构。这在需要同时搜索多个字典并获取适当的键值对映射时非常有用。

import collections

dict1 = {'day1': 'Mon', 'day2': 'Tue'}
dict2 = {'day3': 'Wed', 'day1': 'Thu'}
res = collections.ChainMap(dict1, dict2)

print('Keys = {}'.format(list(res.keys())))
print('Values = {}'.format(list(res.values())))

结果：

扩展

数据映射的应用场景数据映射在数据库操作、数据清洗和深度学习等领域有广泛的应用。例如，在深度学习中，标签映射是指将数据集中的标签从一个类别映射到另一个类别。

方法1：线性映射

线性映射是最基本的映射方法之一，它将一个值范围按比例映射到另一个值范围。假设有一个值范围从a到b，我们想在另一个值范围从c到d中进行映射。可以使用下面的公式来进行线性映射

mapped_value = (value - a) * (d - c) / (b - a) + c

从0到100的值范围映射到-1到1的值范围

def linear_mapping(value, a, b, c, d):
    mapped_value = (value - a) * (d - c) / (b - a) + c
    return mapped_value

original_value = 50
mapped_value = linear_mapping(original_value, 0, 100, -1, 1)
print(mapped_value)

方法2：使用NumPy进行映射

NumPy是一个强大的Python库，提供了许多用于数组和矩阵操作的函数。我们可以使用NumPy提供的函数来进行值范围的映射。下面是一个例子，使用NumPy的interp函数进行线性插值映射

import numpy as np

def numpy_mapping(value, a, b, c, d):
    original_range = np.array([a, b])
    target_range = np.array([c, d])
    mapped_value = np.interp(value, original_range, target_range)
    return mapped_value

original_value = 50
mapped_value = numpy_mapping(original_value, 0, 100, -1, 1)
print(mapped_value)

方法3：使用Funcy库进行映射

Funcy是一个Python库，提供了一系列函数式编程工具。它的map_range函数可以实现值范围的映射，而且代码更为简洁。下面是一个使用Funcy进行值范围映射的例子

from funcy import project

def funcy_mapping(value, a, b, c, d):
    mapped_value = project(value, (a, b), (c, d))
    return mapped_value

original_value = 50
mapped_value = funcy_mapping(original_value, 0, 100, -1, 1)
print(mapped_value)

上面三个例子的输出结果都为0.0