计算机视觉基础：Harris角点检测算法手撕

文章目录

前言
一、Harris角点检测是什么？
二、算法原理
三、代码展示
四、可视化结果
- 1.harris角点检测代码结果展示
- 2.不同阈值和K值下角点检测结果比较
五、实验总结

前言

本次实验旨在全面了解Harris角点检测算法，具体目标包括：
1.理解Harris角点检测的原理和算法。
2.掌握Harris角点检测的编程实现过程。
3.通过比较不同阈值和K值下的检测效果，评估算法的性能和鲁棒性。

一、Harris角点检测是什么？

Harris角点检测是一种用于图像处理和计算机视觉的算法，旨在检测图像中的角点特征。该方法通过计算图像梯度矩阵的特征值来评估局部变化，识别出角点，即图像中灰度变化明显且具有显著特征的位置。Harris角点检测器具有鲁棒性高、计算效率高的特点，广泛应用于目标跟踪、图像配准和三维重建等领域。

二、算法原理

1.角点及角点检测

角点在保留图像图形重要特征的同时，可以有效地减少信息的数据量，使其信息的含量很高，有效地提高了计算的速度，有利于图像的可靠匹配，使得实时处理成为可能。
我们可以直观的概括下角点所具有的特征：

轮廓之间的交点；
对于同一场景，即使视角发生变化，通常具备稳定性质的特征；
该点附近区域的像素点无论在梯度方向上还是其梯度幅值上有着较大变化；

2.Harris角点检测原理

算法的基本思想是在图像上使用一个固定大小的窗口进行滑动，比较滑动前后窗口中像素的灰度变化情况。如果在任何方向上的滑动都引起了较大的灰度变化，那么我们可以认为窗口中存在角点。
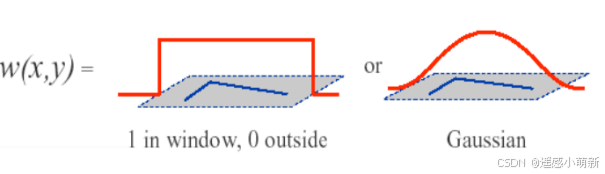
当窗口进行[u,v]的移动时，滑动前后窗口中像素点的灰度变化描述如下： $E(u,v)=\sum_{x_s,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2.$ 其中 $[u, v]$ 表示窗口的偏移量，(x,y)表示窗口内对应的像素坐标位置。窗口的大小决定了窗口内有多少个位置，而 $w (x, y)$ 是窗口函数。最简单的情况是，窗口内所有像素的权重系数都相等，即都为1。
然而，在某些情况下，我们会将窗口函数 $w (x, y)$ 设定为以窗口中心为原点的二维正态分布。如果窗口中心是角点，那么移动前后，该点的灰度变化应该是最显著的，因此该点的权重系数可以设置得更大，表示在窗口移动时，该点对灰度变化的贡献更大；而远离窗口中心（即角点）的点，这些点的灰度变化较为缓和，它们的权重系数可以设置得较小，表示这些点对灰度变化的贡献较小。因此，我们自然地想到使用二维高斯函数来表示窗口函数。因此，通常窗口函数具有以下两种形式：
在这里插入图片描述
根据上述表达式，在窗口滑动到平坦区域时，我们可以想象到灰度不会发生变化，因此 $E (u, v) = 0$ ；而当窗口滑动到纹理丰富的区域时，灰度变化会较大。算法的最终思想就是计算出灰度发生较大变化时所对应的位置，这种较大变化指的是在任意方向上的滑动时的变化情况，而不是单一方向上的变化。
$I (x + u, y + v)$ 泰勒展开可得： $I(x+u,y+v)=I(x,y)+I_xu+I_yv+O(u^2,v^2)$ 当发生微小位移时，忽略无穷小量，写成矩阵形式： $E(u,v)=\sum_w[u,v]\begin{bmatrix}I_x^2&I_xI_y\\I_xI_y&I_y^2\end{bmatrix}\begin{bmatrix}u\\v\end{bmatrix}=[u,v]M\begin{bmatrix}u\\v\end{bmatrix}.$ 所以 $E (u, v)$ 表达式可以更新为： $E(u,v)\cong\begin{bmatrix}u\\v\end{bmatrix}M\begin{bmatrix}u&v\end{bmatrix}_\omega$ 矩阵 $M$ 为: $M(x,y)=\Sigma_w\begin{bmatrix}I_x^2&I_xI_y\\I_xI_y&I_y^2\end{bmatrix}$ $E (u, v)$ 是一个二次型，而由线性代数定理可知：

对于给定二次型 $f=\sum_{i,j=1}^{n}a_{ij}x_{i}x_{j}(a_{ij}=a_{ji})$ ，总有正交变换 $x = P y$ 使得 $f$ 化为标准型 $f=λ_1 y_1^2+λ_2 y_2^2+⋯+λ_n y_n^2$ ,其中 $λ_1，λ_2…λ_n$ 为 $f$ 的矩阵 $A=(a_{ij})$ 的特征值。

因此 $M$ 分解可为： $M=X\Sigma X^T=X[\begin{array}{cc}\lambda_1&0\\0&\lambda_2\end{array}]X^T$

3.角点的判别

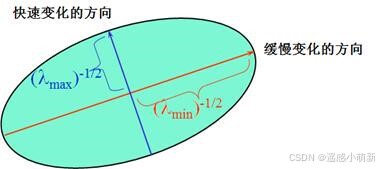
令 $E (u, v)$ =常数，我们可用一个椭圆来描绘这一函数
在这里插入图片描述
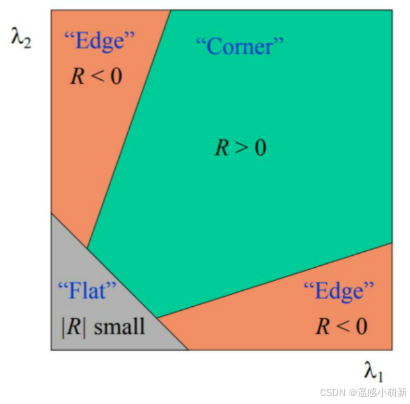
椭圆的长短轴与结构张量 $M$ 的两个特征值相关联。通过对这些情况的判断，我们可以区分出“flat”、“edge”和“corner”这三种区域，因为最直观的印象是（如下图）：

Flat（平坦）：在水平和竖直方向的变化量都较小，即Ix和Iy都较小。
Edge（边缘）：只在水平或者只在竖直方向上有较大的变化，即Ix和Iy中仅有一方较大。
Corner（角点）：在水平和竖直两个方向上都有较大的变化，即Ix和Iy都较大。

可以得出下列结论：
1.特征值都比较大时，即窗口中含有角点
2.特征值一个较大，一个较小，窗口中含有边缘
3.特征值都比较小，窗口处在平坦区域

特征值计算一般比较繁琐，所以把 $M$ 写为：
$M(x,y)=\Sigma_w\begin{bmatrix}I_x^2&I_xI_y\\I_xI_y&I_y^2\end{bmatrix}=\begin{bmatrix}A&C\\C&B\end{bmatrix}.$
定义角点响应函数R（corner response function），采用近似的形式，k为常数，一般取0.04-0.06： $R=detM-k(traceM)^2\\detM=\lambda_1\lambda_2=AB-C^2\\traceM=\lambda_1+\lambda_2=A+B$

三、代码展示

1. 编程思路

代码构造可分五步
在这里插入图片描述
步骤说明：

图像预处理：将彩色图像转换为灰度图像，并可能进行图像平滑处理以减少噪声。
图像梯度计算：使用Sobel算子计算图像的水平和垂直方向的梯度，以获取图像的边缘信息。
结构矩阵计算：根据梯度图像计算每个像素点的结构矩阵，其中包括梯度的幅值和梯度的方向。
计算角点响应函数：根据结构矩阵计算每个像素点的角点响应函数，以判断其是否为角点。
角点标记：根据计算得到的角点响应函数的值，标记图像中检测到的角点，以便后续分析和可视化展示。

2.角点检测代码

import cv2  
import numpy as np  
  
def convert_rgb_to_gray(image):  
    # 将RGB图像转为灰度图像  
    return cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)  
  
def sobel_grad_direction(image_source):  
    # 利用Sobel算子计算图像x，y方向梯度  
    sobel_x = cv2.Sobel(image_source, cv2.CV_32F, 1, 0, ksize=3)  
    sobel_y = cv2.Sobel(image_source, cv2.CV_32F, 0, 1, ksize=3)  
    return sobel_x, sobel_y  
  
def sobel_xx(image_grad_x):  
    # 计算Ixx  
    return image_grad_x * image_grad_x  
  
def sobel_yy(image_grad_y):  
    # 计算Iyy  
    return image_grad_y * image_grad_y  
  
def sobel_xy(image_grad_x, image_grad_y):  
    # 计算Ixy  
    return image_grad_x * image_grad_y  
  
def my_gaussian_blur(src_image, size):  
    # 高斯滤波函数平滑操作  
    return cv2.GaussianBlur(src_image, (size, size), 0)  
  
def harris_response(gauss_xx, gauss_yy, gauss_xy, k):  
    # 计算角点响应值  
    result_data = gauss_xx * gauss_yy - gauss_xy * gauss_xy - k * (gauss_xx + gauss_yy) * (gauss_xx + gauss_yy)  
    return result_data  
  
def check(result_data, src_gray, k_size):  
    # 检查提取角点像素  
    result_image = cv2.cvtColor(src_gray, cv2.COLOR_GRAY2BGR)  # 将灰度图转回RGB图像  
    r = k_size // 2  
    for i in range(r, result_image.shape[0] - r):  
        for j in range(r, result_image.shape[1] - r):  
            if result_data[i, j] > 1e9:  # 这里R阈值设为1e9  
                result_image[i, j] = [0, 0, 255]  # 将附合要求的点颜色设为红色  
    return result_image  
  
# 加载图像  
path1 = r'../Data_Test1/Data/building.png'  
path2 = r'../Data_Test1/Data/chessboard.JPG'  
src_image = cv2.imread(path1)  
  
# 将彩色图转为灰度图  
src_gray = convert_rgb_to_gray(src_image)  
  
# 计算x，y方向梯度  
image_sobel_x, image_sobel_y = sobel_grad_direction(src_gray)  
  
# 计算IXX, IYY, IXY  
image_sobel_xx = sobel_xx(image_sobel_x)  
image_sobel_yy = sobel_yy(image_sobel_y)  
image_sobel_xy = sobel_xy(image_sobel_x, image_sobel_y)  
  
# 高斯平滑，去除噪声  
gaussian_xx = my_gaussian_blur(image_sobel_xx, 3)  
gaussian_yy = my_gaussian_blur(image_sobel_yy, 3)  
gaussian_xy = my_gaussian_blur(image_sobel_xy, 3)  
  
# 计算角点响应值 其中k=0.05  
harris_respond = harris_response(gaussian_xx, gaussian_yy, gaussian_xy, 0.05)  
  
# 提取附合要求的像素  
result_image = check(harris_respond, src_gray, 3)  
  
# 结果展示  
cv2.imshow("Result Image", result_image)  
cv2.waitKey(0)  
cv2.destroyAllWindows()

3.OpenCV接口调用

在opencv，skimage等第三方库中封装了harris角点检测模块，也可以直接调用。
Opencv调用代码如下：

import cv2  
import numpy as np  
  
# 读取图片，并转为灰度图  
path1 = '../Data_Test1/Data/building.png'  
path2 = '../Data_Test1/Data/chessboard.JPG'  
img = cv2.imread(path1)  
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  
cv2.imwrite("building_gray.jpg", gray)  

# Harris角点检测  
dst = cv2.cornerHarris(gray, 2, 3, 0.02)  
  
# dst值大于0.01 * dst.max() 的像素点值赋为 [0,0,255]。  
img[dst > 0.01*dst.max()] = [0, 0, 255]  
cv2.imwrite("building_harris.jpg", img)  
  
cv2.imshow('img', img)  
cv2.waitKey(0)

四、可视化结果

1.harris角点检测代码结果展示

k=0.05,响应阈值为1e9时角点检测结果如图
在这里插入图片描述

2.不同阈值和K值下角点检测结果比较

2.1 在K=0.04时，分别取阈值为0、1e3、1e6、1e9、1e12结果比较：在这里插入图片描述
实验发现：随着阈值提高，检测到的角点数量在减少，角点典型性提高，算法质量得到提高，直至无像素点被识别为角点。
2.2在阈值为1e6时，K分别取0.05,0.10,0.15,0.20,0.25结果比较：

实验发现：较小的K值对边缘敏感，点沿着线分布（如道路）现象显著，而较大的K值则对角点更敏感，点位较为分散，多为角点。随着K值增加，检测到的像素数量减少，角点的典型性提高，直至无像素点被识别。

五、实验总结

通过本次对Harris角点检测算法的学习和实践，我们得到了以下结论：

1．Harris角点检测算法原理理解：
Harris角点检测算法基于图像中局部区域的灰度变化来检测角点。通过计算图像中每个像素点处梯度，进而分析该点在不同方向上的灰度变化程度，以确定其是否为角点。
2.编程实现：
成功使用编程实现了Harris角点检测算法，包括图像预处理、梯度计算、结构矩阵计算、角点响应函数计算和角点标记等步骤。
3.不同参数下结果比较：
通过比较不同阈值和K值下的检测效果，我们发现阈值和K值的设置对检测到的角点数量和质量有显著影响。较高的阈值会减少检测到的角点数量，但可能提高角点的准确性；较低的阈值则会增加角点数量，但可能引入一些非角点区域。
K值的选择同样重要，它决定了对边缘和角点的敏感度。较小的K值对边缘敏感，而较大的K值则对角点更敏感。
4.改进与扩展：
可以考虑通过引入更先进的图像预处理技术来进一步提高Harris角点检测的准确性。
可以尝试对RGB图像某个通道进行算法处理，而非转化为灰度图。
可以探索Harris角点检测算法在实时图像处理系统中的应用，如自动驾驶。