二叉树理论基础:
满二叉树:
树的结点为2的k次-1个
完全二叉树:
最后一层可以不铺满,但是有右必须有左
二叉搜索树:
左节点都小于根节点,右结点都大于根节点
平衡二叉搜索树:
左子树和右子树的高度差不能超过1
存储方式:线性存储/链式存储
树的遍历(递归/迭代):
递归三部曲:
1.确定递归函数的参数和返回值
2.确定终止条件
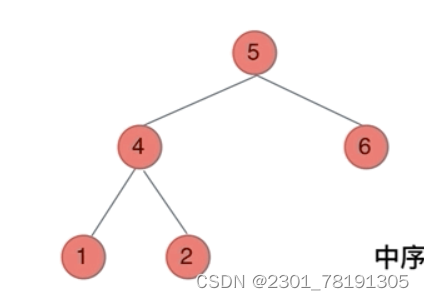
一、前中后遍历(递归法)
根据前中后遍历的特点。中左右/左中右/左右中
拿前序遍历来说:
首先我们要输出该结点的值,然后去递归调用左结点和右结点
代码:
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
traversal(root, list);
return list;
}
public void traversal(TreeNode root, List<Integer> list) {
if(root==null)return;
list.add(root.val);
traversal(root.left,list);
traversal(root.right,list);
}二、前中后遍历(非递归法)
前/后序遍历处理的思路都是一样的(因为前序遍历,经过那一个结点的时候,就会将节点值输出,后序遍历可以由前序遍历通过一系列的转换得到,但是中序遍历,每次都要遍历到最左边,然后菜输出节点值。)
前序遍历:利用栈,将根节点push进去,然后弹出根节点(完成了中),然后将它的右结点、左节点依次入栈。此时在栈顶的元素就是左节点,然后再将左节点pop掉(完成了左),继续将左节点的左右节点入栈。
//定义一个栈存放树节点
Stack<TreeNode> stack=new Stack<>();
//定义一个集合放遍历结果
List<Integer> list=new ArrayList<>();
if(root==null)return list;
stack.push(root);
while(!stack.isEmpty()){
TreeNode node=stack.pop();
list.add(node.val);
if(node.left!=null)stack.push(node.left);
if(node.right!=null)stack.push(node.right);
}后序遍历:就是在前序遍历的基础上左右节点入栈的顺序改变,然后将结果反转。
中序遍历:
先一路向左判断,如果为空了(左结束了),就弹出栈顶的元素(中结束了),然后看右子节点。
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if(root==null)return list;
Stack<TreeNode> stack=new Stack<>();
TreeNode cur=root;
while(cur!=null || !stack.isEmpty()){
if(cur!=null){
stack.push(cur);
cur=cur.left;
}
else{
cur=stack.pop();
list.add(cur.val);
cur=cur.right;
}
}
return list;
}三、二叉树的层序遍历
使用Deque<TreeNode>作为数据结构,返回值是List<List<Integer>>;每一个List<Integer>存放的是每一层的数据。
往队列里面放多少个,那么队列的就有多长。输出和输入的顺序是一致的。遵守队列的先进先出特点。在输出上一层元素的循环中,会往队列里面添加(0->2n个元素)。然后等上一层元素都输出完毕之后,重新计算queue的size,然后while(size--)输出第二层的元素
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> lists=new ArrayList<>();
Queue<TreeNode> queue=new ArrayDeque<>();
if(root!=null){
queue.add(root);
}
while(!queue.isEmpty()){
int size=queue.size();
List<Integer> list=new ArrayList<>();
while(size-->0){
TreeNode node=queue.poll();
list.add(node.val);
if(node.left!=null)queue.add(node.left);
if(node.right!=null)queue.add(node.right);
}
lists.add(list);
}
return lists;
}四、翻转二叉树(曾经有一位应聘者因为不会该问题被淘汰)
使用递归方法:递归三部曲:确立递归函数的返回值和参数、确立终止条件、确立递归逻辑
先将root根节点的左右结点交换,通过swap(TreeNode node)函数交换。然后再递归遍历根节点的左子节点,然后右子结点。这样就是一个先序遍历。后序遍历就是把swap放到最后。
注意:中序遍历(左中右),先调换左子节点的两个结点,然后再调换根节点的左右结点。但是这样左右的顺序就被交换了,之前在左边的子节点跑到了右边。因此第三次还要调换根节点的左子节点。
代码:
public TreeNode mirrorTree(TreeNode root) {
return reverseTree(root);
}
/**
递归三部曲
1.确定递归函数的返回值和参数
2.确定结束条件
3.处理递归逻辑
**/
public TreeNode reverseTree(TreeNode root){
if(root==null)return root;
//递归 翻转左右子节点的结点
reverseTree(root.left);
swap(root);
reverseTree(root.left);
return root;
}
public void swap(TreeNode root){
TreeNode temp=root.left;
root.left=root.right;
root.right=temp;
}五、对称二叉树
我最开始判断是否是对称二叉树是根据:中序遍历 然后从中间向两边走,看两边的元素是否相同,如果相同就说明是对称的。但是没有考虑到有些结点是null的,但是null是无法存在集合中的。
(因此 我想创建一个放字符串的集合 然后把他们的值放进去 如果没有值 就放null 然后比较一下两边的字符串是否相等,还没实现)
因此按照卡尔哥的思想。判断是否是对称树,就要依次对左右结点判断,对相对称的结点判断,会有四种情况:左空 右不空||左不空 右空||左右都空||左右的值不相等。如果左右为空的话就不需要比较剩下的结点了。(这四种情况是起筛选作用的,但是空空的话可以直接返回true)然后剩下最后一种情况,两边值相等,然后就比较子节点。
比较子节点的时候:在按照左左和右右||左右和右左来比较。
代码:
public boolean isSymmetric(TreeNode root) {
return isMirror(root.left,root.right);
}
public boolean isMirror(TreeNode left,TreeNode right){
//比较完了根节点之后
//左空右不空
if(left==null&&right!=null)return false;
//左不空右空
if(left!=null&&right==null)return false;
//都空
if(left==null&&right==null)return true;
//值不相等
if(left.val!=right.val)return false;
boolean leftFlag=isMirror(left.left,right.right);//左左和右右比较
boolean rightFlag=isMirror(left.right,right.left);//左右和右左比较
return leftFlag&&rightFlag;
}六、计算二叉树的深度(层序遍历/递归法)
层序遍历(上面有不多做解释了)
public int calculateDepth(TreeNode root) {
//使用层序遍历
//创建一个队列 来存储结点
Queue<TreeNode> queue=new ArrayDeque<>();
//创建lists存放每层的结果
List<List<Integer>> lists=new ArrayList<>();
if(root!=null)queue.add(root);
while(!queue.isEmpty()){
int size=queue.size();
List<Integer> list=new ArrayList<>();
while(size-->0){
TreeNode node=queue.poll();
list.add(node.val);
if(node.left!=null)queue.add(node.left);
if(node.right!=null)queue.add(node.right);
}
lists.add(list);
}
return lists.size();
}递归法:逻辑:每一个结点的高度就是max(node.left.getHeight(),node.right.getHeight())+1),根据这个逻辑来递归。
递归三部曲:
1.返回值为int(高度) 参数为node
2.终止条件:node==null
3.递归逻辑:
getHeight(TreeNode node){
if(node==null)return 0;
return Math.max(getHeight(node.left),getHeight(node.right))+1;
}
七、计算二叉树的高度(层序遍历/递归)
递归:
注意:计算二叉树的高度时,最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
叶子节点必须是非空的。因此在这里要排除叶子节点是null的情况
递归法:
public int minDepth(TreeNode root) {
return getHeight(root);
}
public int getHeight(TreeNode root) {
if (root == null)
return 0;
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
if (root.left == null) {
return rightHeight + 1;
}
if (root.right == null) {
return leftHeight + 1;
}
return Math.min(leftHeight, rightHeight) + 1;
}中序遍历:
大致思路:在遍历每一层结点的时候,如果遇到一个结点没有左右子节点,那么从根节点到这个结点的距离就是最小高度。
代码:
public int minDepth(TreeNode root) {
// 层序遍历 如果遇到有结点的左右子节点都为空的话 就返回该层的位置
Queue<TreeNode> queue = new ArrayDeque<>();
if (root == null)
return 0;
List<List<Integer>> lists = new ArrayList<>();
queue.add(root);
int distance = 0;
while (!queue.isEmpty()) {
int size = queue.size();
List<Integer> list = new ArrayList<>();
while (size-- > 0) {
TreeNode node = queue.poll();
list.add(node.val);
boolean flag = isAlone(node);
if (flag) {
return lists.size()+1;
}
if(node.left!=null)queue.add(node.left);
if(node.right!=null)queue.add(node.right);
}
lists.add(list);
}
return 0;
}
public boolean isAlone(TreeNode node) {
if (node.left == null && node.right == null)
return true;
else
return false;
}八、完全二叉树的节点个数(层序遍历/利用满二叉树的性质)
层序遍历:遍历每一层的元素,然后把元素都加起来,最后返回。
利用满二叉树的性质:
递归三部曲:1.参数为TreeNode node 返回值为int
2.当node==null的时候,返回0;还有一种情况就是当子树为一颗满二叉树的时候,直接返回2<<leftHeight-1;
3.递归逻辑:如果不满足的话,那么就递归函数 return way(root.left)+way(root.right)+1;
然后再在小子树里面找有没有满足满二叉树性质的。
代码:
public int countNodes(TreeNode root) {
if (root == null)
return 0;
TreeNode left = root.left;
TreeNode right = root.right;
int leftHeight=0;
int rightHeight=0;
while(left!=null){
leftHeight++;
left=left.left;
}
while(right!=null){
rightHeight++;
right=right.right;
}
if(leftHeight==rightHeight){
return (2<<leftHeight)-1;
}
return countNodes(root.left)+countNodes(root.right)+1;
}九、平衡二叉树(递归法/迭代法)
二叉树:任何一个节点的左右节点的高度差值<=1。
递归法:
递归函数的返回值为int,参数为TreeNode root
终止条件:node==null
递归逻辑:
1.当子节点中存在高度插值>1 证明不能是平衡二叉树 直接返回-1。分别对左右子节点讨论
2.当该节点的左右高度差值>1 证明不是平衡二叉树 返回-1
3.都满足,那么直接返回该结点的高度差。return Math.max(leftHeight,rightHeight)+1;