目录
💥1、删除有序数组中的重复项
示例:
可以用快慢指针,快指针表示遍历数组到达的下标位置,慢指针表示下一个不同元素要填入的下标位置,初始时两个指针都指向下标1,这是为了体现慢指针记录不重复的数据个数。
删除重复项和找不重复的项效果是一样的。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int slow = 1;
for (int fast = 1; fast < nums.size(); ++fast)
{
if (nums[fast] != nums[fast - 1])
{
nums[slow++] = nums[fast];
}
}
return slow;
}
};
💥2、数组中出现次数超过一半的数字
方法一:候选法
- 时间复杂度:O(N)
- 空间复杂度:O(1)
初始化一个候选目标val和得票数count,遍历数组,如果当前的得票数count为0的话就选当前在数组中拿到的元素为目标,如果得票数count不为0,有和val相等的元素就给它投一票,遇到不相等的就减一票。 遍历完数组后val就是出现次数超过数组长度一般的数。
- 我们暂且将出现次数超过数组长度一半的数称作众数。数组中如果两个数不相等,就消去这两个数,最坏情况下,每次消去一个众数和一个非众数,那么如果存在众数,最后留下的数肯定是众数
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int>& numbers) {
int val = 0;
int count = 0;
for (int e : numbers)
{
if (0 == count)
{
val = e;
++count;
}
else {
count = val == e ? ++count : --count;
}
}
return val;
}
};
方法二:排序法
- 时间负责度:O(N*logN)
- 空间负责度:O(1)
既然众数的个数超过了数组长度的一半,那有序数组中间位置的数一定就是众数。
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int>& numbers) {
sort(numbers.begin(), numbers.end());
return numbers[numbers.size() / 2];
}
};
💥3、最小栈
定义一个主栈和辅助栈,主栈支持push、pop、top操作,辅助栈用于存相比于栈顶数据更小的或相等的数,主栈pop时如果栈顶数据和辅助栈栈顶数据相等,辅助栈也跟着pop,那么常数时间内检索到的最小元素就是辅助栈栈顶数据。
class MinStack {
public:
MinStack() {}
void push(int val) {
_st.push(val);
if (_minst.empty() || val <= _minst.top())
{
_minst.push(val);
}
}
void pop() {
if (_st.top() == _minst.top())
{
_minst.pop();
}
_st.pop();
}
int top() {
return _st.top();
}
int getMin() {
return _minst.top();
}
private:
stack<int> _st;
stack<int> _minst;
};
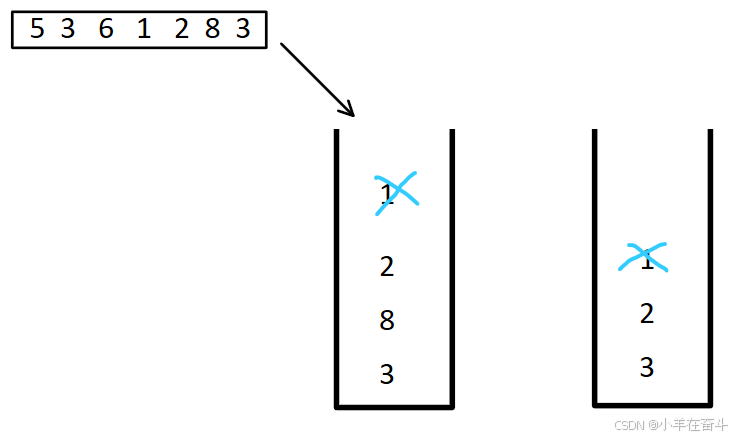
💥4、栈的压入、弹出序列
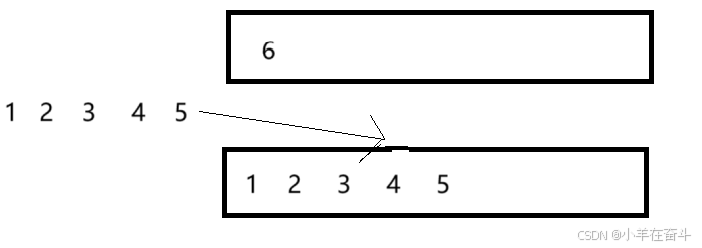
定义一个栈用于压入数据,一个下标用于访问弹出序列。将压入序列依次放入栈中,期间如果某次压入的值和弹出序列的第一个数相等,那么就弹出刚压入的这个数,再++下标。
其中弹出栈中的数时要保证栈不为空,当访问完所有的压入数据后,检查栈是否为空,如果为空则返回真,否则返回假。
class Solution {
public:
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
// write code here
int i = 0;
for (int e : pushV)
{
_st.push(e);
while (!_st.empty() && _st.top() == popV[i])
{
_st.pop();
++i;
}
}
return _st.empty();
}
private:
stack<int> _st;
};
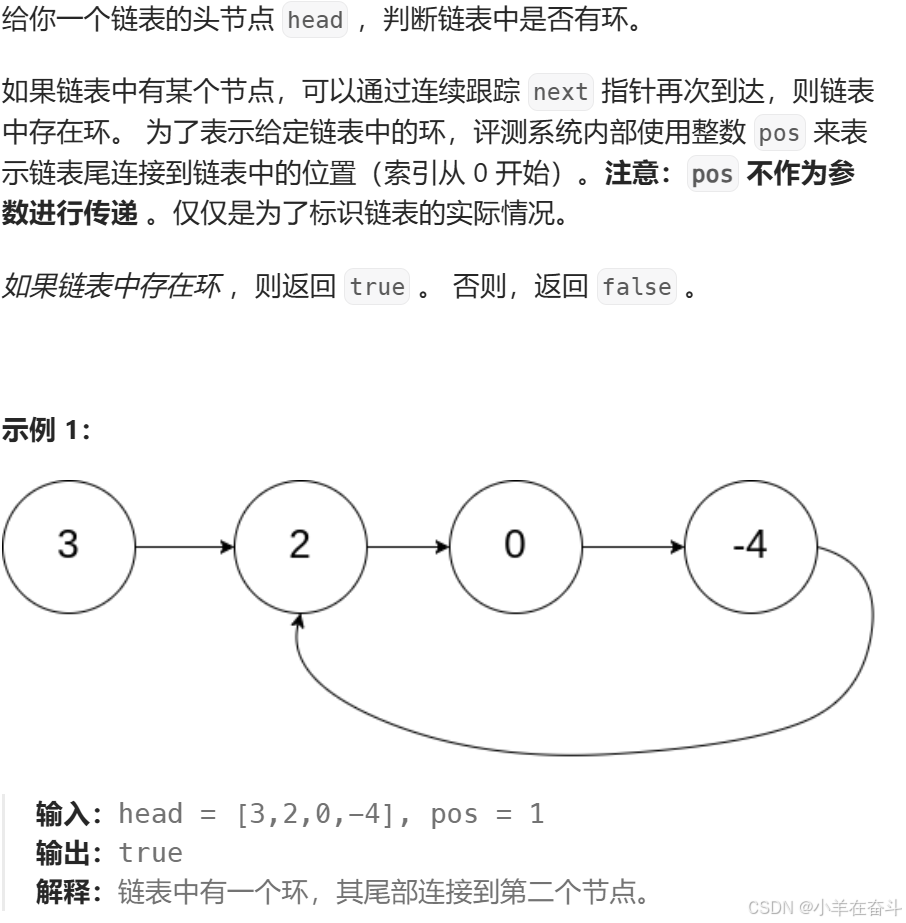
💥5、环形链表
快慢指针法: 快指针和慢指针初始时指向头节点,当快指针指向和快指针指向节点内的next指针不为空时,快指针一次走两步,慢指针一次走一步,快指针入环后走N圈后慢指针入环,当快指针和慢指针相等时说明存在环,如果出循环则说明不存在环。
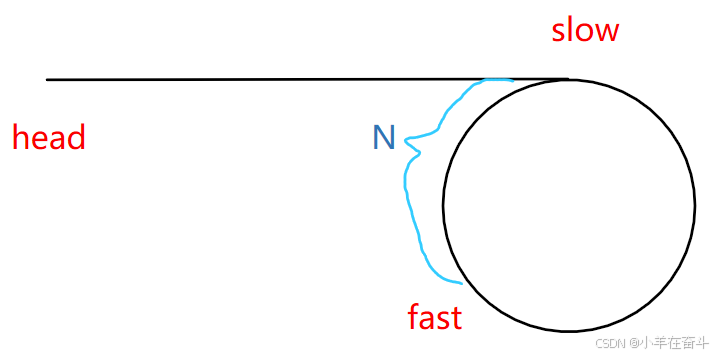
关键的地方是快指针一次走两步,慢指针一次走一步,如果存在环则快指针和慢指针一定会相遇。为什么一定会相遇呢?
如果存在环,假设当慢指针入环时快指针距离此时慢指针的位置为N,则接下来每当快指针追赶慢指针一次,它们的距离就减一,直到减为0,此时快慢指针就相遇了。
bool hasCycle(struct ListNode *head) {
struct ListNode* fast = head, *slow = head;
while (fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
if (fast == slow)
{
return true;
}
}
return false;
}
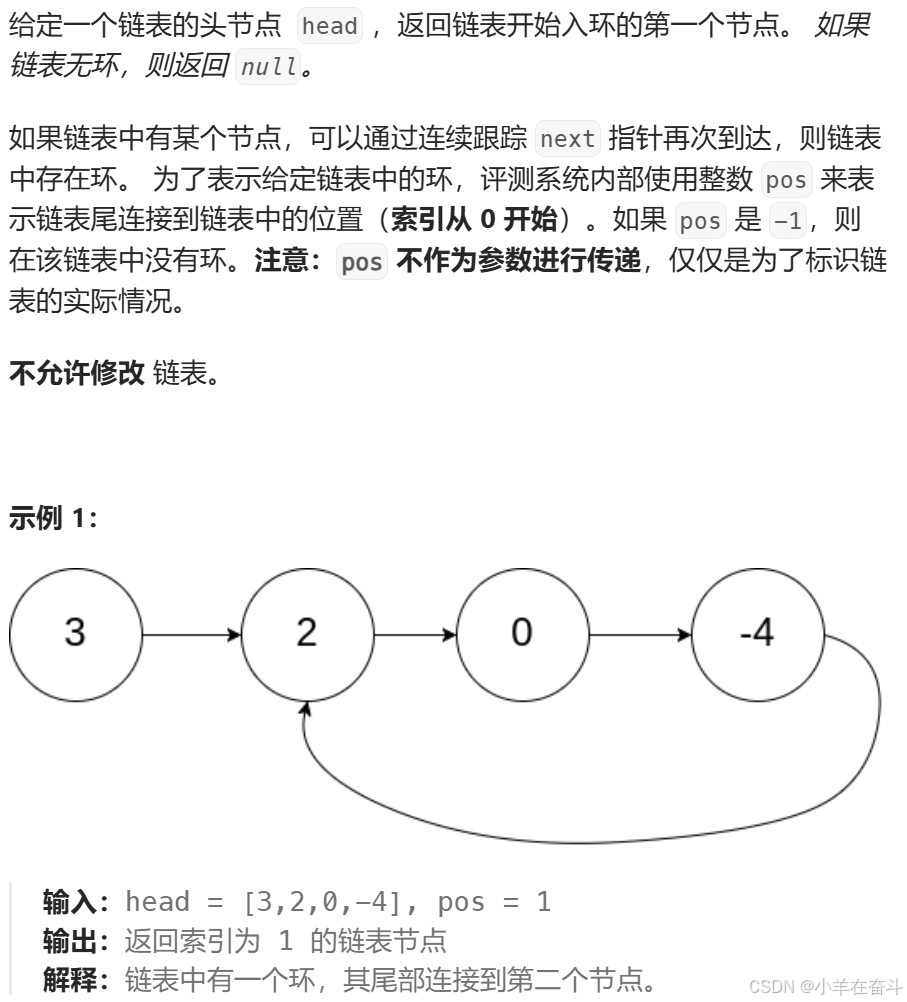
💥6、环形链表 II
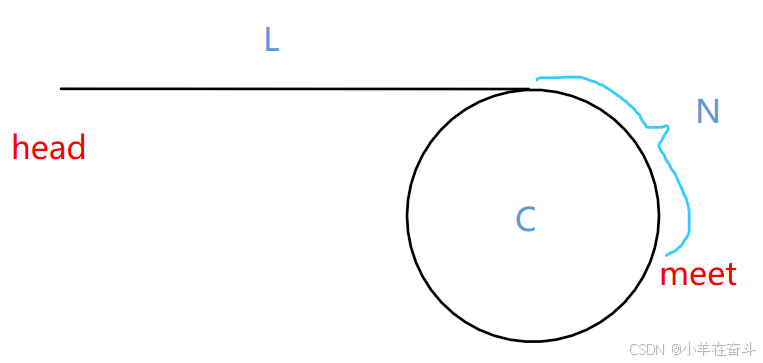
还是快慢指针,当快慢指针相遇时我们让meet指针指向相遇时的节点,然后让头指针head和meet指针一步步地向后走,当两指针相遇时指向的节点就是链表开始入环的第一个节点。为什么这两个指针一定会相遇在链表开始入环的第一个节点?
假设头指针距离链表开始入环的第一个节点的长度为L,meet指针相距链表开始入环的第一个节点的距离是N,环的长度为C,当慢指针入环时快指针走了x圈,因为快指针的速度是慢指针的2倍,那我们可以得到下面的等式:
- 2(L + N) = L + X*C + N
化简得:L = X*C - N,由这个等式可以得出head和meet相遇是必然的。
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode* fast = head, *slow = head;
while (fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
if (fast == slow)
{
struct ListNode* meet = fast;
while (head != meet)
{
head = head->next;
meet = meet->next;
}
return meet;
}
}
return NULL;
}
💥7、用队列实现栈
栈的特点是后进先出,队列的特点是先进先出,用队列实现栈,必须有一个辅助队列在栈数据pop的时候用来导数据,将栈中需要pop的数据放到队列的队头pop。
也就是说用队列实现栈需要两个队列,一个存数据一个导数据,一个为空一个不为空,其中入栈时往不为空的队列中入数据,为空的队列只有一个作用,就是栈pop数据时导数据。
其中队列还有一个重要的特点,就是出队列不会改变数据的相对位置。
typedef struct {
Que q1;
Que q2;
} MyStack;
MyStack* myStackCreate() {
MyStack* pst = (MyStack*)malloc(sizeof(MyStack));
QueueInit(&pst->q1);
QueueInit(&pst->q2);
return pst;
}
void myStackPush(MyStack* obj, int x) {
if (QueueEmpty(&obj->q1))
{
QueuePush(&obj->q2, x);
}
else{
QueuePush(&obj->q1, x);
}
}
int myStackPop(MyStack* obj) {
//假设法
Que* empty = &obj->q1;
Que* noempty = &obj->q2;
if (!QueueEmpty(&obj->q1))
{
empty = &obj->q2;
noempty = &obj->q1;
}
while (QueueSize(noempty) > 1)
{
QueuePush(empty, QueueFront(noempty));
QueuePop(noempty);
}
int top = QueueFront(noempty);
QueuePop(noempty);
return top;
}
int myStackTop(MyStack* obj) {
if (!QueueEmpty(&obj->q1))
{
return QueueBack(&obj->q1);
}
else{
return QueueBack(&obj->q2);
}
}
bool myStackEmpty(MyStack* obj) {
return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}
void myStackFree(MyStack* obj) {
QueueDestroy(&obj->q1);
QueueDestroy(&obj->q2);
free(obj);
}
💥8、用栈实现队列
用两个栈实现队列,这里有两个方法。
方法一:和用两个队列实现栈类似,其中的一个栈用来导数据,因为栈的特点是后进先出,所以将栈中的数据导过来会让数据的相对位置颠倒,所以最后还需要将数据重新导回来才能保证数据的相对位置不变。
typedef int st_data_type;
typedef struct stack
{
st_data_type* arr;
int top;
int capacity;
}stack;
void stack_init(stack* pst)
{
assert(pst);
pst->arr = NULL;
pst->top = pst->capacity = 0;
}
//入栈
void stack_push(stack* pst, st_data_type x)
{
assert(pst);
if (pst->capacity == pst->top)
{
int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;
st_data_type* tmp = (st_data_type*)realloc(pst->arr, newcapacity * sizeof(st_data_type));
if (tmp == NULL)
{
perror("realloc fail!");
return;
}
pst->arr = tmp;
tmp = NULL;
pst->capacity = newcapacity;
}
pst->arr[pst->top] = x;
pst->top++;
}
//出栈
void stack_pop(stack* pst)
{
assert(pst);
assert(pst->top > 0);
pst->top--;
}
//取出栈顶元素
st_data_type stack_top(stack* pst)
{
assert(pst);
assert(pst->top > 0);
return pst->arr[pst->top-1];
}
//销毁
void stack_destroy(stack* pst)
{
assert(pst);
free(pst->arr);
pst->arr = NULL;
pst->capacity = pst->top = 0;
}
//判空
bool stack_empty(stack* pst)
{
assert(pst);
return pst->top == 0;
}
//获取元素个数
int stack_size(stack* pst)
{
assert(pst);
return pst->top;
}
typedef struct {
stack st1;
stack st2;
} MyQueue;
MyQueue* myQueueCreate() {
MyQueue* pqu = (MyQueue*)malloc(sizeof(MyQueue));
stack_init(&pqu->st1);
stack_init(&pqu->st2);
return pqu;
}
void myQueuePush(MyQueue* obj, int x) {
if (stack_empty(&obj->st1))
{
stack_push(&obj->st2, x);
}
else
{
stack_push(&obj->st1, x);
}
}
int myQueuePop(MyQueue* obj) {
stack* empty = &obj->st1;
stack* noempty = &obj->st2;
if (stack_empty(&obj->st2))
{
empty = &obj->st2;
noempty = &obj->st1;
}
while (stack_size(noempty) > 1)
{
stack_push(empty, stack_top(noempty));
stack_pop(noempty);
}
int top = stack_top(noempty);
stack_pop(noempty);
while (!stack_empty(empty))
{
stack_push(noempty, stack_top(empty));
stack_pop(empty);
}
return top;
}
int myQueuePeek(MyQueue* obj) {
stack* empty = &obj->st1;
stack* noempty = &obj->st2;
if (stack_empty(noempty))
{
empty = &obj->st2;
noempty = &obj->st1;
}
while (!stack_empty(noempty))
{
stack_push(empty, stack_top(noempty));
stack_pop(noempty);
}
int top = stack_top(empty);
while (!stack_empty(empty))
{
stack_push(noempty, stack_top(empty));
stack_pop(empty);
}
return top;
}
bool myQueueEmpty(MyQueue* obj) {
return stack_empty(&obj->st1) && stack_empty(&obj->st2);
}
void myQueueFree(MyQueue* obj) {
stack_destroy(&obj->st1);
stack_destroy(&obj->st2);
free(obj);
}
方法二:正是因为栈后进先出的特点,我们可以不用将导过来的数据再导回去,一个栈专门用来入数据,另一个栈专门用来出数据。 很显然这种方法更为简单。
typedef int st_data_type;
typedef struct stack
{
st_data_type* arr;
int top;
int capacity;
}stack;
void stack_init(stack* pst)
{
assert(pst);
pst->arr = NULL;
pst->top = pst->capacity = 0;
}
//入栈
void stack_push(stack* pst, st_data_type x)
{
assert(pst);
if (pst->capacity == pst->top)
{
int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;
st_data_type* tmp = (st_data_type*)realloc(pst->arr, newcapacity * sizeof(st_data_type));
if (tmp == NULL)
{
perror("realloc fail!");
return;
}
pst->arr = tmp;
tmp = NULL;
pst->capacity = newcapacity;
}
pst->arr[pst->top] = x;
pst->top++;
}
//出栈
void stack_pop(stack* pst)
{
assert(pst);
assert(pst->top > 0);
pst->top--;
}
//取出栈顶元素
st_data_type stack_top(stack* pst)
{
assert(pst);
assert(pst->top > 0);
return pst->arr[pst->top-1];
}
//销毁
void stack_destroy(stack* pst)
{
assert(pst);
free(pst->arr);
pst->arr = NULL;
pst->capacity = pst->top = 0;
}
//判空
bool stack_empty(stack* pst)
{
assert(pst);
return pst->top == 0;
}
//获取元素个数
int stack_size(stack* pst)
{
assert(pst);
return pst->top;
}
typedef struct {
stack pushst;
stack popst;
} MyQueue;
MyQueue* myQueueCreate() {
MyQueue* pst = (MyQueue*)malloc(sizeof(MyQueue));
stack_init(&pst->pushst);
stack_init(&pst->popst);
return pst;
}
void myQueuePush(MyQueue* obj, int x) {
stack_push(&obj->pushst, x);
}
int myQueuePop(MyQueue* obj) {
if (stack_empty(&obj->popst))
{
while (!stack_empty(&obj->pushst))
{
stack_push(&obj->popst, stack_top(&obj->pushst));
stack_pop(&obj->pushst);
}
}
int top = stack_top(&obj->popst);
stack_pop(&obj->popst);
return top;
}
int myQueuePeek(MyQueue* obj) {
if (stack_empty(&obj->popst))
{
while (!stack_empty(&obj->pushst))
{
stack_push(&obj->popst, stack_top(&obj->pushst));
stack_pop(&obj->pushst);
}
}
return stack_top(&obj->popst);
}
bool myQueueEmpty(MyQueue* obj) {
return stack_empty(&obj->pushst) && stack_empty(&obj->popst);
}
void myQueueFree(MyQueue* obj) {
stack_init(&obj->pushst);
stack_init(&obj->popst);
free(obj);
}
💥9、设计循环队列
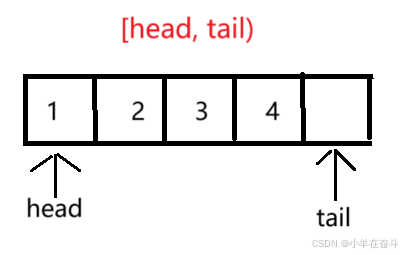
这里我们用数组来实现循环队列会相对简单一些,让head指向第一个位置,让tail指向最后一个元素的下一个位置。假设队列长度为K,我们开K + 1个空间,多开一个空间是为了方便区分队列为空和队列为满。也可以在结构体中多加一个变量用来计数。因为如果不多开一个空间,队列为空时是head == tail,队列为满时也是head == tail,无法区分。多开一个空间后,队列为满就是head == (tail + 1) % (k + 1).
当tail越界时我们对其模K+1,让tail指向下标为0的位置。
typedef struct {
int* a;
int head;
int tail;
int k;
} MyCircularQueue;
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->head == obj->tail;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return obj->head == (obj->tail + 1) % (obj->k + 1);
}
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* pq = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
pq->a = (int*)malloc(sizeof(int)*(k + 1));
pq->head = pq->tail = 0;
pq->k = k;
return pq;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if (myCircularQueueIsFull(obj))
{
return false;
}
obj->a[obj->tail++] = value;
obj->tail %= obj->k + 1;
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if (myCircularQueueIsEmpty(obj))
{
return false;
}
obj->head++;
obj->head %= obj->k + 1;
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if (myCircularQueueIsEmpty(obj))
{
return -1;
}
return obj->a[obj->head];
}
int myCircularQueueRear(MyCircularQueue* obj) {
if (myCircularQueueIsEmpty(obj))
{
return -1;
}
return obj->a[(obj->tail - 1 + obj->k + 1) % (obj->k + 1)];
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
free(obj);
}
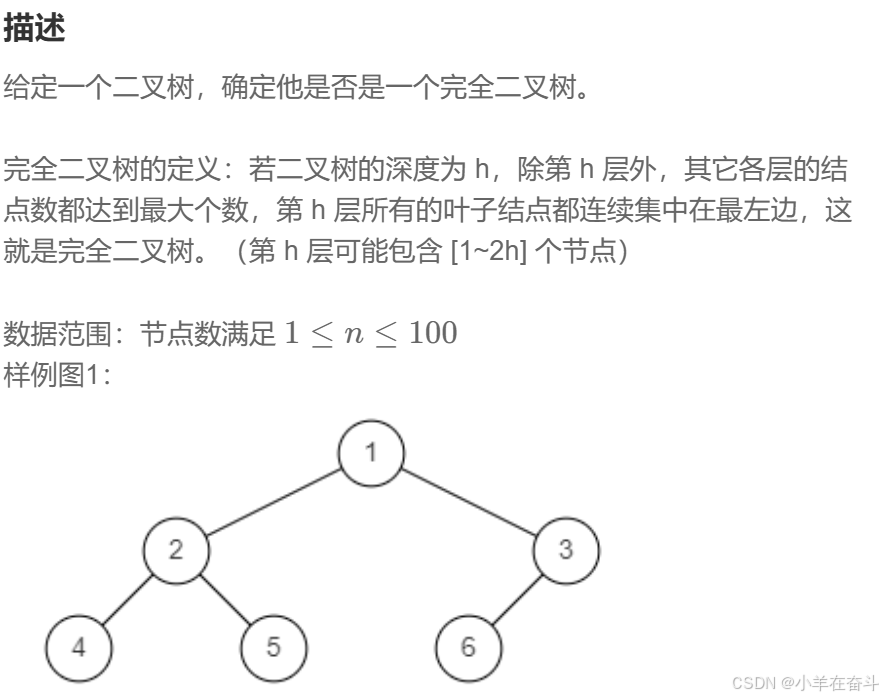
💥10、判断二叉树是否是完全二叉树
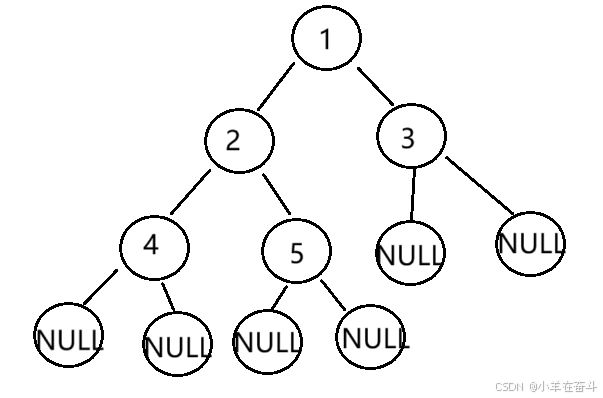
层序遍历二叉树,当某次pop到非节点时不再入节点,然后不断pop,如果是完全二叉树,则pop到的全是非节点;如果是非完全二叉树,则某次会pop到节点。
完全二叉树:
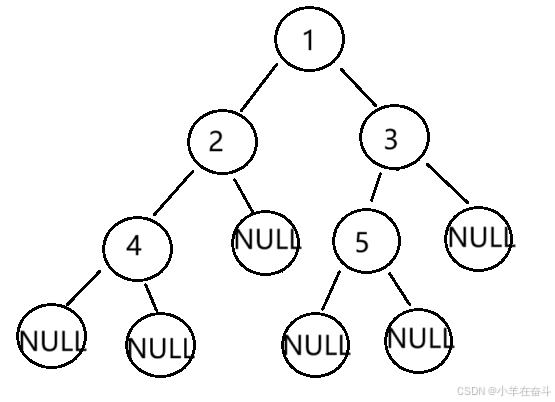
非完全二叉树:
class Solution {
public:
bool isCompleteTree(TreeNode* root) {
// write code here
if (root == nullptr)
{
return true;
}
_qu.push(root);
while (!_qu.empty())
{
TreeNode* front = _qu.front();
_qu.pop();
if (front == nullptr)
{
break;
}
_qu.push(front->left);
_qu.push(front->right);
}
while (!_qu.empty())
{
TreeNode* front = _qu.front();
_qu.pop();
if (front != nullptr)
{
return false;
}
}
return true;
}
private:
queue<TreeNode*> _qu;
};
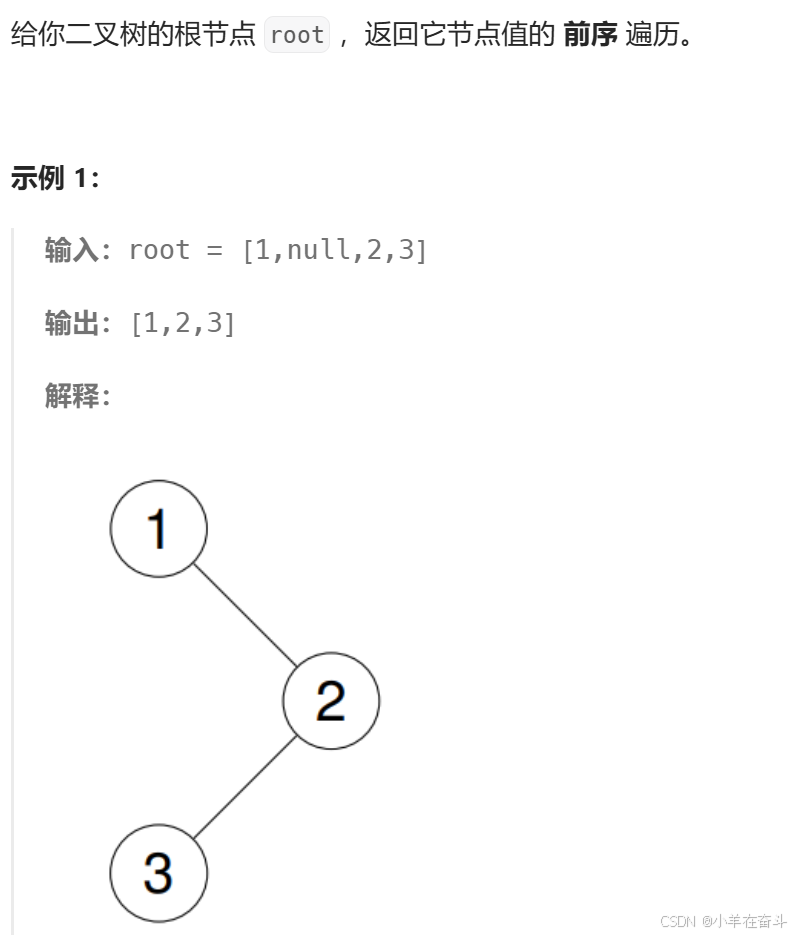
💥11、二叉树的前序遍历
每次递归都会建立新的栈帧空间,不同的栈帧空间内相同的变量之间互不影响,而我们需要的是每次函数递归都要改变下标,所以需要传地址。
int TreeSize(struct TreeNode* root)
{
if (root == NULL)
{
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
void PreOrder(struct TreeNode* root, int* arr, int* pi)
{
if (root == NULL)
{
return;
}
//每次递归都会建立新的栈帧空间,不同的栈帧空间内相同的变量之间互不影响,
//而我们需要的是每次函数递归都要改变下标,所以需要传地址。
arr[(*pi)++] = root->val;
PreOrder(root->left, arr, pi);
PreOrder(root->right, arr, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
*returnSize = TreeSize(root);
int* arr = (int*)malloc(*returnSize * sizeof(int));
int i = 0;
PreOrder(root, arr, &i);
return arr;
}