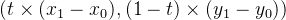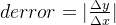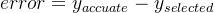Bootstrap

直线画法-Bresenham‘s algorithm原理和最优实现

目录

定点+向量法/朴素画法

Bresenham算法

核心思想

实现一、 f(x)

实现二、derror

实现三、还可再优化！

Games101中引用的stackoverflow的写法

更多

整数运算真的快于浮点预算吗？

优化到极致的方案

参考

定点+向量法/朴素画法

void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) { 
    for (float t=0.; t<1.; t+=.01) { 
        int x = x0 + (x1-x0)*t; 
        int y = y0 + (y1-y0)*t; 
        image.set(x, y, color); 
    } 
}

这种绘制法应该是自己第一次绘制直线时最为直观的做法，但是不够好。体现在什么地方呢？

  1. 该函数使用了浮点，而在大部分架构下整数运算会快于浮点运算
  2. t的取值，假定 x_1-x_0 是个无比巨大的数，t取0.01的话采样频率就过低了，会出现断点
  3. 如果 |x1 - x0| ≠ |y1 - y0|，则 x 和 y 的增量不同步，导致线条变形或拉伸

左侧使用朴素画法的顶点处处理得便不是很好，因为固定步长向量是

(t\times(x_1-x_0),(1-t)\times(y_1-y_0))

所以无法很好拟合。而bresenham算法则甩开这个包袱，因此表现更好。

Bresenham算法

图中红点为实际选取绘制像素点，绿点为 x.5 的比较点 ， 蓝点是 f(x) 上的实际准确点，圆圈为红点的“管辖范围”，只要蓝点进入则说明当前x处选取点为该红点

核心思想

  • 像素点都位于整数点上，两个像素中点必为 *.5 格式

  • 点 f(x) 若大于 y.5 则取 y+1 点绘制，否则取 y 点绘制

实现一、 f(x)

int y = y0;
for(int x=x0;x<=x1;x++){
	if(f(x)>y+0.5)y+=1;  //如果没过中点，保持原有y
  
  if (steep) { 
        image.set(y, x, color); 
  } else { 
        image.set(x, y, color); 
  } 
}

注意steep!

bool steep = false; 
if (std::abs(x0-x1)<std::abs(y0-y1)) { 
    std::swap(x0, y0); 
    std::swap(x1, y1); 
    steep = true; 
} 
if (x0>x1) { 
    std::swap(x0, x1); 
    std::swap(y0, y1); 
}

Bresenham算法实际上可以看作是对于一条直线的采样，那么选取更长的轴线，我们的采样次数越多，我们得到的直线也会越准确。此处通过比较 dx 与 dy 大小得出 steep ，最终决定以谁为x进行计算。所以绘制时要将这个影响还回来。

实现二、derror

为什么要引入derror，我直接算出f(x)再比较不香吗？

  • 每跨一点算一遍f(x)
  • 每跨一点加上固定长度 derror

f(x)终究是个多项式公式，，显然后者是更优解

derror

我们将之定义为基底上每过一个单位长度，实际线段上在高度上所变化的长度

derror=|\frac{\Delta y}{\Delta x}|

error=y_{accuate}-y_{selected }

注意：error并不是两个点之间的距离，而是差值，可正可负

我们定义刚开始 error=0

每次x+1，则有 error+=derror

每次当 error>0.5 时便说明它超出了上一个红点的管辖范围进入到了下一个红点的管辖范围，要通过-1来重新计算与当前红点的距离。

int dx = x1-x0; 
int dy = y1-y0; 
float derror = std::abs(dy/float(dx)); 
float error = 0; 
int y = y0; 
for (int x=x0; x<=x1; x++) { 
    if (steep) { 
        image.set(y, x, color); 
    } else { 
        image.set(x, y, color); 
    } 
    error += derror; 
    if (error>.5) { 
        y += (y1>y0?1:-1); 
        error -= 1.; 
    } 
}

实现三、还可再优化！

关注浮点运算

float derror = std::abs(dy/float(dx)); 
if (error>.5)

既然都是比较而没有实际准度要求，何不都乘以 2*dx ，化浮点为整数！

void line_tinyRender(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) { 
    bool steep = false; 
    if (std::abs(x0-x1)<std::abs(y0-y1)) { 
        std::swap(x0, y0); 
        std::swap(x1, y1); 
        steep = true; 
    } 
    if (x0>x1) { 
        std::swap(x0, x1); 
        std::swap(y0, y1); 
    } 
    
    int dx = x1-x0; 
    int dy = y1-y0; 
    int derror2 = std::abs(dy)*2; 
    int error2 = 0; 
    int y = y0; 
    for (int x=x0; x<=x1; x++) { 
        if (steep) { 
            image.set(y, x, color); 
        } else { 
            image.set(x, y, color); 
        } 
        error2 += derror2; 
        if (error2 > dx) { 
            y += (y1>y0?1:-1); 
            error2 -= dx*2; 
        } 
    } 
}

Games101中引用的stackoverflow的写法

void line_games101(int x1, int y1, int x2, int y2, TGAImage &image, TGAColor color)
{
	int x, y, dx, dy, dx1, dy1, px, py, xe, ye, i;

	dx = x2 - x1;
	dy = y2 - y1;
	dx1 = fabs(dx);
	dy1 = fabs(dy);
	px = 2 * dy1 - dx1;
	py = 2 * dx1 - dy1;

	// 挑选x轴作为基底轴
	if (dy1 <= dx1)
	{
		//始终从左到右
		if (dx >= 0)
		{
			x = x1;
			y = y1;
			xe = x2;
		}
		else
		{
			x = x2;
			y = y2;
			xe = x1;
		}
		image.set(x, y, color);

		for (i = 0; x < xe; i++)
		{
			x = x + 1;
			// 误差小于0，同个y
			if (px < 0)
			{
				px = px + 2 * dy1;
			}
			// 误差大于0，更改y
			else
			{
				if ((dx < 0 && dy < 0) || (dx > 0 && dy > 0))
				{
					y = y + 1;
				}
				else
				{
					y = y - 1;
				}
				px = px + 2 * (dy1 - dx1);
			}
			image.set(x, y, color);
		}
	}
	//选取y轴作为基底
	else
	{
		if (dy >= 0)
		{
			x = x1;
			y = y1;
			ye = y2;
		}
		else
		{
			x = x2;
			y = y2;
			ye = y1;
		}
		image.set(x, y, color);
		for (i = 0; y < ye; i++)
		{
			y = y + 1;
			if (py <= 0)
			{
				py = py + 2 * dx1;
			}
			else
			{
				if ((dx < 0 && dy < 0) || (dx > 0 && dy > 0))
				{
					x = x + 1;
				}
				else
				{
					x = x - 1;
				}
				py = py + 2 * (dx1 - dy1);
			}
			//            delay(0);
			image.set(x, y, color);
		}
	}
}

Games101引用的是https://stackoverflow.com/a/16405254/29859442 该问题下的第一个回答，该实现与课程质量之间并无关联。为了便于比较，笔者做了一些更改。

实话实说，当时看到这串line_draw代码的时候整个人都不好了。多层的if-else和for嵌套，不仅不利于理解，而且过多的分支预测也会拖慢代码执行的速度。

究其原因，有几个可以提升的点

  1. 翻转坐标系本身，而不是切换基底。换句话说，就是始终以x轴为基底，只不过当y方向上投影更长时，我们将x-y轴倒置过来（体现为swap函数），进而节省下一个if-else的判定（代码长度减半）
  2. 使用if-else+swap而非if-else语句中嵌套复制
  3. 使用三元运算符
  4. 将共同项 +2*dy1 提到判定之外去（更有利于理解）

最后我们使用gprof来对以上两种算法性能进行测试

更多

整数运算真的快于浮点预算吗？

Bresenham直线生成算法是由Jack Elton Bresenham在1962年于IBM开发的，在当时的计算机架构下整数运算普遍快于浮点数，因而催生出了Bresenham算法。在现代计算机架构下还有必要使用该算法吗?

Floating point vs integer calculations on modern hardwarehttps://stackoverflow.com/questions/2550281/floating-point-vs-integer-calculations-on-modern-hardware#2550430

复制其中一个高赞回复

For example (lesser numbers are faster),

64-bit Intel Xeon X5550 @ 2.67GHz, gcc 4.1.2 -O3

short add/sub: 1.005460 [0]
short mul/div: 3.926543 [0]
long add/sub: 0.000000 [0]
long mul/div: 7.378581 [0]
long long add/sub: 0.000000 [0]
long long mul/div: 7.378593 [0]
float add/sub: 0.993583 [0]
float mul/div: 1.821565 [0]
double add/sub: 0.993884 [0]
double mul/div: 1.988664 [0]

32-bit Dual Core AMD Opteron(tm) Processor 265 @ 1.81GHz, gcc 3.4.6 -O3

short add/sub: 0.553863 [0]
short mul/div: 12.509163 [0]
long add/sub: 0.556912 [0]
long mul/div: 12.748019 [0]
long long add/sub: 5.298999 [0]
long long mul/div: 20.461186 [0]
float add/sub: 2.688253 [0]
float mul/div: 4.683886 [0]
double add/sub: 2.700834 [0]
double mul/div: 4.646755 [0]

As Dan pointed out, even once you normalize for clock frequency (which can be misleading in itself in pipelined designs), results will vary wildly based on CPU architecture (individual **ALU/FPU performance**, as well as actual number of ALUs/FPUs available per core in superscalar designs which influences how many independent operations can execute in parallel -- the latter factor is not exercised by the code below as all operations below are sequentially dependent.)

以下是本人的运算结果

13th Gen Intel(R) Core(TM) i5-13500H @ 2.60 GHz gcc 13.1.0 -O3

short add/sub: 0.000001 [0]
short mul/div: 3.805635 [1]
long add/sub: 0.000000 [0]
long mul/div: 4.451186 [0]
long long add/sub: 0.000000 [0]
long long mul/div: 4.364804 [0]
float add/sub: 0.694168 [0]
float mul/div: 3.515955 [0]
double add/sub: 1.014292 [0]
double mul/div: 3.987668 [0]

可见还是会存在一些影响，Bresenham直线生成算法仍有其存在必要性

优化到极致的方案

void drawLine(Point2Di p0,  Point2Di p1)
{
    bool yLonger=false;
    int shortLen=p1.y-p0.y;
    int longLen=p1.x-p0.x;
    if (abs(shortLen)>abs(longLen)) {
        swap(shortLen, longLen);
        yLonger=true;
    }
    int decInc = longLen==0 ?  decInc=0 : ((shortLen << 16) / longLen);

    if (yLonger) {
        p0.y*=imageSide;
        p1.y*=imageSide;
        if (longLen>0)
            for (int j=0x8000+(p0.x<<16);p0.y<=p1.y;p0.y+=imageSide, j+=decInc)
                buffer[p0.y + (j >> 16)] = 255;  // or a call to your painting method
        else
            for (int j=0x8000+(p0.x<<16);p0.y>=p1.y;p0.y-=imageSide, j-=decInc)
                buffer[p0.y + (j >> 16)] = 255;  // or a call to your painting method
    }
    else
    {
        if (longLen>0)
            for (int j=0x8000+(p0.y<<16);p0.x<=p1.x;++p0.x, j+=decInc)
                buffer[(j >> 16) * imageSide + p0.x] = 255;  // or a call to your painting method
        else
            for (int j=0x8000+(p0.y<<16);p0.x>=p1.x;--p0.x, j-=decInc)
                buffer[(j >> 16) * imageSide + p0.x] = 255;  // or a call to your painting method
    }
}

Drawing lines with Bresenham's Line Algorithmhttps://stackoverflow.com/a/52859805/29859442

更多优化相关讨论

Simple speed up of Lesson 1 · Issue #28 · ssloy/tinyrenderer · GitHubFirst off, amazing content. But changing the line drawing function, so that it does not check if it is steep, within the for loop, almost speeds it up by 2x, with -O3 on. So, with sacrificing for a little extra code bloat, if one changes...https://github.com/ssloy/tinyrenderer/issues/28

参考

Lesson 1: Bresenham’s Line Drawing Algorithmhttps://github.com/ssloy/tinyrenderer/wiki/Lesson-1:-Bresenham%E2%80%99s-Line-Drawing-Algorithm

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
keycloak~社区登录中数据导入的方式
已测全新首发小利特惠/生活缴费/电话费/油卡燃气/等充值业务类源码
一款功能齐全的iOS混淆工具介绍及功能详解
浅析ethx网卡控制函数ioctl实现具体流程
灰色系统理论：优势分析、生成数与灰色建模
计算机毕业设计Springboot汽车零部件ERP系统 基于Spring Boot的汽车零部件供应链管理系统设计与实现 Spring Boot框架下的汽车零部件企业资源规划系统开发
keycloak~自定义登出接口
ssm535基于SSM的游戏资源管理系统+vue
深入理解css浮动
Welcome to the Real World! It sucks!
;